lec

A=an-1Sn-1+…+a1S1+a0S0+a-1S-1+…+a-mS-m ( 1 )

Целая часть

Дробная часть

где S – основание системы, ai – одна из цифр алфавита этой системы счисления.

При сокращенной записи числа основание системы счисления подразумевается, а цифры целой и дробной части разделяются точкой:

A=an-1 an-2…a1a0 . a-1 a-2…a-m

Целая часть Дробная часть

Каждая цифра в записи числа называется разрядом. Для двоичных чисел вместо термина разряд часто используют термин бит. Каждый левый разряд имеет вес в S раз больший, чем предыдущий. Крайний правый разряд имеет наименьший вес и называется младшим разрядом. Крайний левый разряд имеет наибольший вес и называется старшим разрядом.

Пусть на запись числа отведено n+m разрядов, из них n на целую часть и m на дробную часть. Число рассматривается как число без знака. Определим максимальное и минимальное число, которое может быть записано в этой разрядной сетке:

Максимальное число Amax = (Sn – 1) + (1 - S-						m=2
m)		n=3
	максимальная целая часть	9	9	9	.	9	9
	максимальная дробная часть
	Например, для десятичной системы при

n=3 и m=2 максимальное число

Amax = (103–1) + (1-10-2) = (1000-1) + (1–0.01) = 999 + 0.99 = 999.99

Для получения записи максимального числа необходимо занести во все разряды наибольшую цифру системы счисления.

Минимальное	минимальная целая часть	отличное от	n=3				m=2
нуля число Amin=		0 + S-m	0	0	0	.	0	1
Например,	минимальная дробная часть	для десятичной системы при n=3 и
m=2 минимальное число
	Amin = 10-2 = 0.01

Для получения записи минимального числа необходимо занести в младший разряд единицу, а в остальные разряды нули.

Количество различных комбинаций цифр Nк определяет количество различных по значению чисел, которые могут быть записаны в заданных

разрядах:

Nк = Sm+n

Для рассмотренного примера количество десятичных чисел Nк=105

При работе с технической документацией и анализе машинных программ приходится выполнять преобразования чисел из одной системы счисления в другую. Общие правила преобразования будут рассмотрены ниже.

11

В таблице приведена запись первых 20-ти чисел в разных системах счисления:

A10	A2	A8	A16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9

A10	A2	A8	A16
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13

2. Преобразования из любой системы счисления в десятичную систему

Выполняется по полиномиальной записи числа (1). Основание исходной системы и значения цифр рассматриваются как десятичные числа. Все операции выполняются по правилам десятичной арифметики. Рас-

смотрим примеры преобразования чисел в десятичную систему.

A[2] = 101.1 = 1*22 + 0*21 + 1*20 + 1*2-1 = 4 + 0 + 1 + 0.5 = 5.5[10] A[16] = AB.8 = 10*161 + 11*160 + 8*16-1 = 160 + 11 + 0.5 = 171.5[10]

A[8] = 173.4 = 1*82 + 7*81 + 3*80 + 4*8-1 = 64 + 56 + 3 + 0.5 = 123.5[10]

Удобно сразу же над цифрами исходного числа проставлять вес разрядов

8	4	2	1	0.5	0.25
A[2] = 1 0 0 1 .				1	1 = 8 + 1 + 0.5 + 0.25 = 9.75[10]

3. Преобразования из десятичной системы счисления в любую другую систему

Преобразование выполняется отдельно для целой и дробной части числа. Все операции выполняются по правилам десятичной арифметики. Основание новой системы рассматривается как десятичное число.

Преобразование целой части выполняется путем последовательного деления целой части на основание новой системы. На каждом шаге вычисляется целая часть и остаток от деления. Остатки и есть значение цифр числа в новой системе счисления. Полученные остатки записываются в новой системе счисления. На первом шаге будет получена младшая цифра. Процесс продолжается, пока очередная целая часть не окажется меньше основания новой системы счисления. Эта целая часть есть старшая цифра числа.

Правила перевода следуют из формы записи числа в позиционной системе счисления:

n-1

1

n-2

0

a0

→ a0

Шаг 1

A10

= an-1S

+…+a1S

+ a0

| :S an-1S

+…+ a1S +

S

Целая часть

Остаток

Шаг 2

A10

= an-1Sn-2+…+a2S1+ a1

| : S an-1Sn-3 +…+ a2S0 +

a1

→ a1

S

Целая часть

Остаток

12

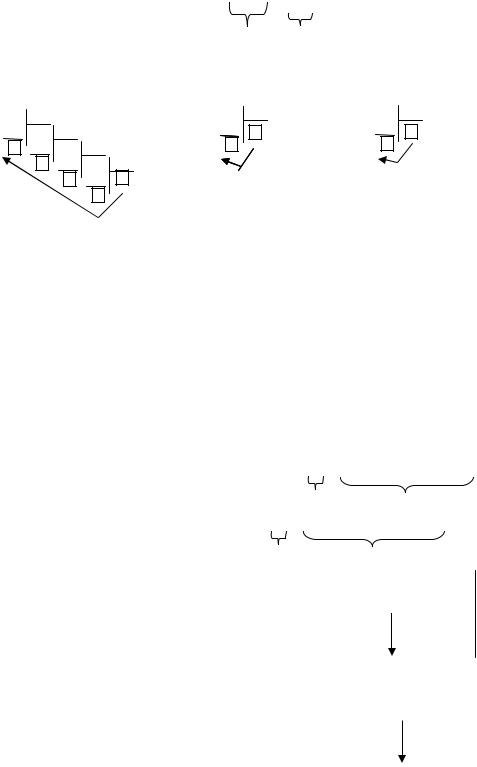
Шаг n-1		A10 = an-1S1+ an-2			| : S an-1 +		an−2	→ an-2
							S
					Целая часть Остаток
Пример: 23[10] → ?[2]					Пример: 23[10] → ?[8]				Пример: 23[10] → ?[16]
23	2				23	8			23	16
22	11	2			16	2			16	1
1	10	5	2	2	7				7
	1	4	2		старшинство				старшинство
		1	2	1
			0		цифр				цифр
	старшинство цифр
	10111[2]				27[8]					17[16]

Преобразование дробной части выполняется путем последовательного умножения дробной части на основание новой системы. На каждом шаге выделяется новая целая часть и новая дробная часть. Последовательность целых частей дает значение цифр числа в новой системе счисления. На первом шаге будет получена старшая цифра дробной части в новой системе. Процесс продолжается до получения заданного количества значащих цифр или нулевого значения дробной части.

Правила перевода следуют из формы записи числа в позиционной системе счисления:

Шаг 1 A10 = a-1S-1 + a-2S-2 +…+a-mS-m | * S a-1 + a-2S-1 + … +a-mS-m+1

Целая часть Дробная часть

Шаг 2 A10 = a-2S-1 +…+a-mS-m+1 | * S a-2 + a-3S-1 + … +a-mS-m+2

Целая часть	Дробная часть
			Целая часть				Дробная часть
Пример: 0.125[10]→?[2]
				0		125 * 2
В данном примере преобразование завершено при
			0			250 * 2
получении нулевой дробной части.
			0			500 * 2
0.125[10]→0.001[2]
			1			000
			Целая часть				Дробная часть
Пример: 0.55[10]→?[16]			0				55 * 16
					8		800 *16
В данном примере преобразование проводится до					C		800 *16
получения трех значащих цифр дробной части.					C		800
0.55[10]→0.8СС[16]

4. Преобразования из любой системы счисления в любую другую систему счисления

Необходимо преобразовать число из системы счисления S1 в систему счисления S2. Это наиболее общий вариант преобразования чисел из одной системы счисления в другую. Преобразование выполняется по тем же правилам, что и из десятичной системы в любую другую. Операции выполняются по правилам арифметики в системе счисления S1, что соз-

13

дает определенные неудобства. На практике такие преобразования выполняются через промежуточное преобразование в десятичную систему:

Число в системе S1 Æ Число в десятичной системе Æ Число в системе S2

Такая схема позволяет выполнять все операции в привычной для человека десятичной системе.

Важным для практики случаем является преобразование из двоичной системы в восьмеричную или шестнадцатеричную систему и обратное преобразование. Такие преобразования можно выполнить без промежуточного преобразования в десятичную систему.

5. Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Эти преобразования наиболее просты, так как восьмеричные и шестнадцатеричные числа представляют собой не что иное, как компактную форму записи двоичных чисел. Преобразование базируются на том, что основание одной системы является степью двойки основания другой системы:

23 = 8, поэтому восьмеричную цифру можно представить группой из трех двоичных цифр. Группа из трех двоичных цифр называется триадой;

24 = 16, поэтому шестнадцатеричную цифру можно представить группой из четырех двоичных цифр. Группа из четырех двоичных цифр называется тетрадой.

Преобразование «2 → 8». Двигаясь от точки влево и вправо разбить цифры исходного двоичного числа на триады. При необходимости дополнить число слева и справа не значащими нулями. Каждую триаду

	заменить		восьмеричной цифрой.
	0 0 1 0 1 1 1 1 0 . 1 0 1 1 1 0				На рисунке приведен пример преобразо-
					вания двоичного числа 1011110.10111 в
	1	3	6 . 5	6	восьмеричное число 136.56. Для образо-
					вания триад слева добавлены два нуля, а

справа один.

Преобразование «2 → 16». Правила аналогичны преобразованию «2 → 8», но исходное двоичное число разбивается на тетрады.

	0001 1011 1110 . 0011 1100			На рисунке приведен пример преобразо-
				вания двоичного числа 110111110.001111
	1	B E . 3	C	в шестнадцатеричное число 1BE.3C. Для
				образования тетрад слева добавлены три

нуля, а справа два.

Преобразование «8 → 2». Это преобразование противоположно преобразованию «2 → 8». Каждая цифра исходного восьмеричного числа заменяется триадой, содержащей двоичный эквивалент восьмеричной цифры. Незначащие левые и правые нули можно отбросить.

	2	0	3	•	4	На рисунке приведен пример преобра-
						зования восьмеричного числа 203.4 в
	010	000	011	•	100	двоичное число 10000011.1. Слева от-
						брошен один незначащий ноль, а спра-

ва - два незначащих нуля.

14

Преобразование «16 → 2». Это преобразование противоположно «2 → 16». Каждая цифра исходного шестнадцатеричного числа заменяется тетрадой, содержащей двоичный эквивалент шестнадцатеричной цифры.

	Незначащие левые и правые нули можно отбросить.
	7	C	F	•	A	На рисунке приведен пример преобра-
						зования	шестнадцатеричного		числа
	0111	1100	1111	•	1010	7CF.A	в	двоичное	число
						11111001111.101. Слева и справа от-

брошено по одному незначащему нулю.

Для получения двоичной тетрады, эквивалентной восьмеричной цифре, можно использовать правило “421”, в основе которого лежит представление числа в виде суммы степеней двойки. В триаде необходимо записать единицы на местах цифр, сумма которых дает значение восьмеричной цифры. На местах остальных цифр записать ноль.

Примеры: 7[8] = 4 + 2 +1 111[2]

3[8] =			2 +1	011[2]
6[8]	= 4		+ 2	110[2]
5[8]	=	4	+ 1	101[2]

Для получения двоичной тетрады, эквивалентной шестнадцатеричной цифре, можно использовать правило “8421”. В тетраде необходимо за-

писать единицы на местах цифр,		сумма которых дает значение шестна-
дцатеричной цифры. На местах остальных цифр записать ноль
Примеры: F[16] = 15[10] = 8 + 4 + 2 + 1 1111[2]
C[16] = 12[10] =	8 + 4	1100[2]
D[16] = 13[10] =	8 + 4	+ 1 1101[2]
9[16] = 9[10] =	8 +	1 1001[2]

6. Двоичная арифметика

Правила арифметических операций во всех позиционных системах одинаковы и основываются на таблицах сложения, вычитания и умножения одноразрядных чисел. В силу наибольшей распространенности двоичной системы более детально остановимся на ней.

Таблица. сложения Таблица. вычитания Таблица. Умножения

	заем
0 + 0 = 0	10 – 1 = 1	0 * 0 = 0
0 + 1 = 1	1 – 1 = 0	0 * 1 = 0
1 + 0 = 1	0 – 0 = 0	1 * 0 = 0
1 + 1 =10 перенос	1 – 0 = 1	1 * 1 = 1

	Сложение двоичных чисел. Выполняется
	поразрядно, начиная с младшего разряда. В		1 1 1 0 1 . 0 1	29.25
	сложении участвуют одноименные разряды	+
			1 0 1 1 . 1 0	11.5
	слагаемых и перенос в текущий разряд. Ре-
		1 0 1 0 0 0 . 1 1		40.75
	зультатом является сумма в текущем разряде

и перенос в следующий разряд. В зависимости от значения слагаемых перенос будет равен 0 (нет переноса) или 1 (есть перенос). ЭВМ имеет специальное устройство, предназначенное для сложения двоичных чисел. Это устройство называется сумматором. Сумматор реализует сложе-

15

1 1 0 1 1 . 1 0 27.5 - 1 1 0 1 . 0 1 13.25 1 1 1 0 . 0 1 14.25

ние через комбинацию логических операций. Логические операции будут рассмотрены позже.

Вычитание двоичных чисел. Выполняется поразрядно, начиная с младшего. При необходимости выполняется заем двойки из соседнего старшего разряда. ЭВМ обычно не имеет специального вычитающего устройства. За счет применения специальных кодов операция вычитания заменяется на операцию сложения.

Умножение двоичных чисел. Выполняется путем последовательного умножения цифр множителя на множимое и сложение частичных сумм. Количество цифр в дробной части результата равно суммарному количеству цифр в дробных частях сомножителей. Пример умножения приведен на Рис.1. В ЭВМ умножение реализуется путем сдвига множимого и прибавление его к сумме, если цифра множителя равна единице.

*	1 0 1 . 1 0	5.5	1100.011 : 101.1 = 11000.11 : 1011 = 10.01
	1 0 . 0 1	2.25	12.375 :	5.5	123.75 : 55	2.25
	+ 1 0 1 1 0
+	0 0 0 0 0		_11000.11	1011
+ 0 0 0 0 0
			1011	10.01
1 0 1 1 0
		12.375	_1011
1 1 0 0. 0 1 1 0
			1011
	2+2 = 4 цифры
			0
	Рис. 1				Рис. 2

Деление двоичных чисел. Реализуется путем последовательных умножений цифр результата на делитель и вычитания из делимого. Пример деления приведен на Рис.2.

При выполнении операций сложения и вычитания вручную удобнее пользоваться восьмеричной или шестнадцатеричной системой. Рассмотрим особенности выполнения операций в этих системах счисления.

Если при сложении одноименных разрядов и переноса получено число N<S, то оно берется в качестве суммы разряда, а перенос в следующий разряд равен 0. Если получено число N≥S, то в качестве суммы берется разность N-S и формируется единица переноса в следующий разряд. При сложении нескольких чисел сумма одноименных разрядов может превысить основание системы счисления в несколько раз. В этом

Пример: 267[8]+136[8]=425[8]	Пример: 2FA[16]+3B2[16]=6AC[16]
2 6 7 183[10]	2 F A	762[10]
+1 3 6 94[10]	+ 3 B 2	946[10]
4 2 5 277[10]	6 A C 1708[10]
13-8=5

10-8=2	16	26-16=10

случае необходимо пользоваться общим правилом: в качестве суммы берется остаток от целочисленного деления N/S, а значение переноса в следующий разряд есть целая часть от деления N/S.

При вычитании разрядов при необходимости берется заем из старшего разряда. Вычитание производится из суммы S+Ai, где Ai – значение i-го разряда вычитаемого. Значение разряда, из которого производился заем, уменьшается на 1.

Пример: 231[8]-67[8]=142[8]	Пример: 243[16]-1FA[16]=49[16]
2 3 1 153[10]	2 4 3			579[10]
- 6 7 55[10]		- 1 F A		506[10]
1 4 2 277[10]	4 9			73[10]
(8+1)-7=2				(16+3)-10=9
(8+2)-6=4	(16+3)-15=4

Операции умножения и деления в этих системах менее удобны для ручного выполнения, так как требуют знания таблиц умножения для восьмеричных или шестнадцатеричных чисел.

17

ЛОГИЧЕСКИЕ ОСНОВЫ ПОСТРОЕНИЯ ЭВМ

1. Логические переменные, функции и операции

ЭВМ преобразует информацию, представленную в виде двоичных кодов. Каждый разряд кода принимает значение 0 или 1. Именно поэтому для описания функционирования устройств ЭВМ широко используется аппарат алгебры логики.

Алгебра логики изучает логические функции. Функция Y(x0,x1,…,xn) является логической, если ее аргументы и она сама принимают только одно из двух значений: “истина” или “ложь”. Значение “истина” принято кодировать как 1, а значение “ложь” - как 0.

Аргументы логической функции называют логическими переменными. В алгебре логики логические переменные принято обозначать строчными латинскими буквами, а функции – прописными латинскими буквами.

Часто логические переменные и функции называют булевыми от имени английского математика Джорджа Буля, занимавшегося разработкой основ алгебры логики.

Логические функции строятся на основе элементарных логических операций. Так как значение логических переменных и функций ограничено значениями 0 и 1, определение смысла логических операций удобно производить табличным способом. В таблице приводятся все комбинации значений переменных и результат операции. Таблицу такого рода в алгебре логики называют таблицей истинности. Приведем таблицы истинности для элементарных логических операций.

1.Логическое отрицание (НЕ, инверсия: x

xx

			0		1
	1			0				выражениях
	2. Логическое умножение (И, конъюнкция):
	x1 х2.
	Иногда эта операция обозначается через знак ум-
	ножения или его пропуск: х1•х2 или х1х 2.							логическихв
		0		1		0
			x1	x2		x1 x2
		0		0		0
								операций
		1		0		0
	3. Логическое			сложение (ИЛИ, дизъюнкция):
		1		1		1
	x1 x2.							Старшинство
	Иногда эта операция обозначается через знак сло-
	жения: х1+х2.
			x1	x2		x1 x2
		0		0		0
		0		1		1
		1		0		1
		1		1		1

Выражение, содержащее логические переменные и логические операции, называется логическим выражением. Порядок выполнения операций определяется их старшинством (приоритетом). Приоритет логических операций приведен на рисунке. Порядок выполнения операций

18

можно регулировать скобками. Операции в скобках выполняются в первую очередь.

Подобно алгебраическим операциям, для логических операций существуют законы их выполнения, свойства и следствия из них.

Основные законы логических операций:

Переместительный закон: a b=b a; a•b=b•a Сочетательный закон: a (b c) = (a b) c = b (a c)

a•(b•c) = (a•b)•c = b•(a•c).

Распределительные законы: a•(b c) = a•b a•с (первый) a (b•c) = (a b)•(a с) (второй)

Закон двойственности (закон де Моргана):

a •b

= a b

= a •b

a b

Закон двойственного отрицания:

= a

a

Закон исключения:

a

= 1

a

Закон противоречия:

a•

= 0

a

Основные свойства логических операций:

Свойства логического умножения:

0•a = 0,

1•a = a

Свойства логического сложения:

0 a = a,

1 a = 1

Свойство повторения:

a•a• a•…• a•a=a; a a a … a a=a.

Из перечисленных законов и свойств вытекает широко использующихся

следствия:
Cклеивание	a • x a •x = a • (x x) = a • 1 = a
	(a x) • (a x) = a (x •x) = a • 0 = a
Неполное склеивание:
	a • x a •x a = a • (x x 1) = a • 1 = a
Поглощение:	a a • x = a • (1 x) = a • 1 = a
	a a •x = a • (1 x) = a • 1 = a
	a •(a x) = a•a a•x = a a•x = a•(1 x) = a•1 = a
	a •(a x) = a•a a•x = a a•x = a•(1 x) = a•1 = a

Устройства ЭВМ реализуют логические функции. Для сокращения элементов в устройстве логическую функцию максимально упрощают. Упрощение логической функции преследует цель сократить количество переменных и операций до минимума. Этот процесс называют минимизацией. Минимизация проводится на основе законов, свойств и следствий алгебры логики. Рассмотрим пример минимизации:

Y = x 2 x 1 x 0 + x 2 x 1 x 0 + x 2 x 1 x 0 + x 2 x 1 x 0 =

(

x 2

x 1

x 0

+

x 2

x 1

x 0 ) + (

x 2

x 1 x 0 + x 2 x 1 x 0 ) =

x 0

(

+

x 2

) + x 1 x 0 (

+ x 2 ) =

x 0 1 + x 1 x 0 1 =

x 1

x 2

x 2

x 1

x 0

+ x 1 x 0 = x 0 (

+ x 1 ) = x 0 1 = x 0

x 1

x 1

2. Способы описания логических функций

Применяются три основных способа описания логических функций: аналитический, табличный и графический.

19

При аналитическом способе функция записываются в виде логического выражения.

При табличном способе функция записывается в виде таблицы истинности. Число строк в таблице истинности равно числу комбинаций переменных, т.е 2n, где n - число логических переменных. Таблицу истинности можно составить по аналитической записи путем подстановки всех комбинаций значений переменных.

Преобразование таблицы истинности в аналитическую запись выполняется по методу совершенной дизъюнктивной нормальной формы (СДНФ) или методу совершенной конъюнктивной нормальной формы (СКНФ).

СДНФ –функция, образованная сложением всех конституант единицы. Конституанта единицы составляется для тех комбинаций переменных, на которых функция равна единице. Конституанта единицы – это логическое умножение всех переменных, причем переменные, имеющие значение 0, берутся с инверсией. Составим аналитическую запись логической функции двух переменных по заданной таблице истинности.

Номер комбинации	x1	x2	Y
1	0	0	0
2	0	1	1
3	1	0	1
4	1	1	0

В рассматриваемом примере логических переменных две, т.о. количество комбинаций 22=4. Комбинациям в строчках 2 и 3 соответствует единичное значение функции. Именно для них составляются конституанты 1.В результате сложения конституант 1 получим аналитическую запись функции по методу СДНФ:

Y = x1 • x2 + x1 •x2

Метод СДНФ целесообразно применять, когда в таблице истинности преобладают нулевые значения функции.

СКНФ –функция, образованная умножением всех конституант нуля. Конституанта нуля составляется для тех комбинаций переменных, на которых значение логической функции равно нулю. Конституанта нуля – это логическое сложение всех переменных, причем переменные, имеющие значение 1, берутся с инверсией. Составим аналитическую запись логической функции по таблице истинности, рассмотренной в предыдущем примере. Комбинациям в строчках 1 и 4 соответствует нулевое значение функции. Именно для них составляются конституанты 0. Путем умножения конституант 0 получим СКНФ:

Y = (x1 + x2 ) • ( x 1 + x 2)

Метод СКНФ целесообразно применять, когда в таблице истинности преобладают единичные значения функции.

Логические функции считаются тождественными, если их значения совпадают при всех комбинациях аргументов. Т.о. тождественность логических функций может быть проверена путем сопоставления их таблиц истинности.

20