лесная биометрия

Таблица 14. Вычисление критерия согласия Пирсона χ2 (диаметры)

	xi		fi				~			~		2		~	2
							fi			fi − fi		(fi − ~fi )		(fi −~ fi	)
		До	ук-	После		До укруп-		После						fi
		рупнения		укрупне-		нения		укрупне-
				ния				ния
	14,45		0			3,6
	17,65		3		3	6,0		9,6		–6,6		43,56		4,54
	20,85		11		11	11,6		11,6		–0,6		0,36		0,03
	24,05		29		29	21,2		21,2		7,8		60,84		2,87
	27,25		39		39	28,8		28,8		10,2		104,04		3,61
	30,45		32		32	33,6		33,6		–1,6		2,56		0,08
	33,65		33		33	32,8		32,8		0,2		0,04		0,00
	36,85		23		23	26,6		26,6		–3,6		12,96		0,49
	40,05		10		10	18,0		18,0		–8,0		64,00		3,56
	43,25		9		9	10,0		10,0		–1,0		1,00		0,10
	46,45		3		11	5,0		7,8		3,2		10,24		1,31
	49,65		4			2,0
	52,85		2			0,6
	56,05		2			0,2
	59,25		0			0,0
	Сумма		200		200	200,0		200,0		0,0				16,59

При составлении табл. 14 эмпирические и теоретические частоты вариационного ряда диаметров можно взять из табл. 12. Далее следует объединить интервалы таким образом, чтобы теоретические частоты в укрупненных классах были не меньше пяти. Дальнейшие расчеты (три последние колонки табл. 14) выполняем, используя эмпирические и теоретические частоты, полученные после укрупнения классов. Сумма, полученная в последней колонке таблицы, и будет статистикой Пирсона χ2. Теперь, пользуясь табл. 5 приложения, найдем соответствующий квантиль распределения Пирсона χ2, чтобы, сравнивая его с вычисленной статистикой χ2, проверить нулевую гипотезу. Уровень значимости (вероятность отклонения правильной нулевой гипотезы) возьмем α = 0,05. С учетом объединения интервалов и того, что мы оценили два параметра нормального распределения (σ и m) по материалам наших экспериментальных данных, вычислим число степеней свободы, пользуясь формулой (26):

γ = k −ρ−1 =10 −2 −1 = 7 .

Определив необходимые параметры, найдем квантиль распре-

40

деления Пирсона χ20,05;7 = 14,067 по табл. 5 прил. Так как вычисленная статистика Пирсона χ2 = 16,59 превышает табличное значение, то мы отклоняем нулевую гипотезу, т. е. распределение диаметров деревьев в древостое не подчиняется закону нормального распределения.

Аналогичным образом вычислим критерий Пирсона для распределения высот деревьев в древостое (табл. 15).

Таблица 15. Вычисление критерия согласия Пирсона χ2 (высоты)

xi		fi				~		~	2	~	2
						fi		fi − fi	(fi − ~fi )	(fi −~ fi	)
	До	ук-	После		До укруп-		После			fi
	рупнения		укрупне-		нения		укрупне-
			ния				ния
16,45		0			0,0
17,45		3			0,4
18,45		2			0,8
19,45		2			2,6
20,45		6		13	6,0		9,8	3,2	10,24	1,04
21,45		7		7	13,2		13,2	–6,2	38,44	2,91
22,45		22		22	22,4		22,4	–0,4	0,16	0,01
23,45		21		21	29,4		29,4	–8,4	70,56	2,40
24,45		36		36	34,8		34,8	1,2	1,44	0,04
25,45		44		44	32,8		32,8	11,2	125,44	3,82
26,45		29		29	25,8		25,8	3,2	10,24	0,40
27,45		17		17	16,8		16,8	0,2	0,04	0,00
28,45		9		11	8,8		8,8	2,2	4,84	0,55
29,45		2			4,2		6,2	–6,2	38,44	6,20
30,45		0			2,0
Сумма		200		200	200,0		200,0	0,0		17,37

Сравнивая полученную статистику Пирсона χ2 = 17,37 с квантилем распределения Пирсона χ2 = 16,59, приходим к выводу, что и в данном случае следует отклонить нулевую гипотезу, так как вычисленное значение превышает табличное. Таким образом, и распределение высот деревьев в сосновом древостое не подчиняется закону нормального распределения. В связи с этим вопрос о виде распределения диаметров и высот деревьев в древостое остается открытым. Следовательно, надо выдвигать и проверять с помощью критериев согласия статистические гипотезы в отношении других теоретических распределений до тех пор, пока подходящее распределение не будет найдено. Этот процесс связан с большим количеством вычислительных

41

работ, и поэтому его лучше выполнять с помощью вычислительной техники и специальных статистических программ.

Анализ распределения случайных величин с помощью ПЭВМ

Анализ распределения случайных величин с помощью пакета Statistica 6.0 можно выполнить следующим образом.

1.Запустить программу Statistica и открыть файл с данными, как описано в подразделе 0.

2.Выбрав опцию «Настройка Распределения» из меню «Статистика», открыть диалоговое окно «Distribution Fitting», содержащее список распределений, для которых можно выполнить вычисления. Из данного списка надо выбрать распределение и нажать кнопку «OK».

3.В открывшемся диалоговом окне «Fitting Continuous distributions» или «Fitting Discrete Distributions» в зависимости от того,

какое распределение – непрерывное или дискретное – выбрано, нажать кнопку «Variables». После того как на экране появится еще одно диалоговое окно, содержащее список переменных, выбрать какуюнибудь переменную и нажать кнопку «OK» для возврата в окно настройки распределений.

4.Далее во вкладке «Parameters» при необходимости можно отредактировать такие поля, как «Number of categories» – число интервалов при группировке данных, «Lower limit» – нижняя граница первого интервала, «Upper limit» – верхняя граница последнего интервала, а также поля, содержащие параметры распределения.

5.Для выполнения вычислений надо нажать кнопку

«Summary: Observed and expected distribution» на вкладке «Quick». На экране появится таблица, содержащая эмпирические и теоретические частоты (рис. 10). В данной таблице в колонке «Upper Boundary» приведены верхние границы интервалов; в колонке «Observed Frequency»

–эмпирические частоты; в колонке «Cumulative Observed» – накопленные эмпирические частоты; в колонке «Percent Observed» – эмпирические частоты, выраженные в процентах от общего количества наблюдений; «Cumul. % Observed» – накопленные эмпирические частоты, выраженные в процентах; «Expected Frequency» – теоретические частоты; «Cumulative Expected» – накопленные теоретические частоты; «Percent Expected» – теоретические частоты, выраженные в процентах; «Cumul. % Expected» – накопленные теоретические частоты,

42

выраженные в процентах; «Observed – Expected» – отклонение эмпирических частот от теоретических. Кроме того, в окне результатов (рис. 10) приводится информация, необходимая для проверки нулевой гипотезы о согласованности эмпирического и теоретического распределений. Это статистика Пирсона χ2 – величина «Chi-Square», число степеней свободы – «df» и вероятность совершения ошибки первого рода (вероятность отклонения справедливой нулевой гипотезы) – «p».

Рис. 10. Результаты вычислений, выполненых с помощью программы Statistica, для нормального распределения

6. Если на той же вкладке «Quick» нажать кнопку «Plot of observed and expected distribution», на экране появится график, на кото-

ром будут сравниваться эмпирическое (изображено в виде гистограммы) и теоретическое распределения (рис. 11). На этом же графике приведена информация для проверки гипотезы о согласованности эмпирического и теоретического распределений с помощью критерия Пирсона.

Рассмотрим процесс анализа распределения случайной величины на примере диаметров и высот деревьев. С этой целью выполним расчеты для всех непрерывных распределений, поддерживаемых пакетом Statistica. Для этого, воспользовавшись кнопкой «Variables» из диалогового окна «Fitting Continuous distributions», выбрать переменную «D» – диаметры. Установить необходимые параметры для формирования вариационного ряда, отредактировав соответствующие поля на вкладке «Parameters». Для диаметров установить

43

следующие значения: «Number of categories» – 13; «Lower limit» – 16,05; «Upper limit» – 57,65. Далее, выбирая по очереди различные теоретические распределения с помощью поля с выпадающим спи-

ском «Distribution» в диалоговом окне «Fitting Continuous distributions», выполнить расчеты. Полученные результаты свести в табл. 16.

Рис. 11. Сравнение эмпирического и теоретического распределений с помощью программы Statistica

Таблица 16. Анализ распределения диаметров деревьев в древостое

Распределение	Название	Критерий	Число	Вероятность
	распределения в	Пирсона χ2	степеней	совершения
	программе Sta-		свободы	ошибки
	tistica			1-го рода
Нормальное	Normal	17,68750	7	0,01346
Равномерное	Rectangular	125,75918	10	0,00000
Экспоненциальное	Exponential	489,59517	9	0,00000
Гамма	Gamma	6,35506	7	0,49896
Лог-нормальное	Log-normal	3,51516	6	0,74195
Хи-квадрат	Chi-Square	11,82968	9	0,22308

Анализ полученных результатов показывает, что в отношении трех распределений (гамма, лог-нормальное, хи-квадрат) гипотезу

44

можно принять. Гипотезы, выдвинутые в отношении других распределений, следует отвергнуть. Из трех распределений, которые хорошо подходят к экспериментальным данным, лучшим следует считать лог-нормальное распределение, так как вероятность совершения ошибки 1-го рода для него максимальная.

Аналогичным образом выполним расчеты для вариационного ряда высот. Полученные результаты приведены в табл. 17.

Таблица 17. Анализ распределения высот деревьев в древостое

Распределение	Название	Критерий	Число	Вероятность
	распределения в	Пирсона χ2	степеней	совершения
	программе Sta-		свободы	ошибки 1-го
	tistica			рода
Нормальное	Normal	13,02254	7	0,07156
Равномерное	Rectangular	131,97281	10	0,00000
Экспоненциальное	Exponential	1591,34797	5	0,00000
Гамма	Gamma	17,99613	7	0,01199
Лог-нормальное	Log-normal	21,15575	7	0,00355
Хи-квадрат	Chi-Square	301,86952	11	0,00000

В данном случае гипотезы в отношении всех распределений, кроме нормального, следует отвергнуть, так как для них вероятность сделать при этом ошибку ниже, чем уровень значимости α = 0,05.

В рассматриваемых примерах с помощью программы Statistica были получены несколько иные значения, чем ранее, когда мы подробно рассматривали процесс вычисления теоретических частот и проверку гипотезы о нормальном распределении диаметров и высот. Это вызвано тем, что в программе Statistica параметры нормального распределения оценивались на основании исходных данных без выполнения группировки. В рассматриваемом ранее примере вычисления выполнялись по данным интервальных вариационных рядов, что всегда связано с потерей точности. Кроме того, при вычислениях функции нормального распределения программа Statistica использует аппроксимирующие алгоритмы, а в первом варианте расчета применялись табличные значения функции нормального распределения. С учетом сказанного, целесообразно принять во внимание результаты, полученные с помощью программы Statistica, и принять гипотезу о нормальном распределении высот.

КОРРЕЛЯЦИОННЫЙ АНАЛИЗ

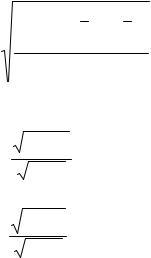
В предыдущих разделах высоты и диаметры анализировались по отдельности, вне связи друг с другом. Однако в природе многие случайные величины в той или иной степени связаны друг с другом. Для того чтобы оценить тесноту связи между случайными величинами, удобно использовать коэффициент корреляции. Его можно вычислить по формуле

k

∑ fi (xi − x) ( yi − y)

R =	i=1		.	(27)
		n Sx S y

Данный показатель оценивает тесноту связи между случайными величинами в случае линейных зависимостей, однако в природе чаще встречаются нелинейные. В таких случаях коэффициент корреляции не может выразить всю полноту связи. Для нелинейных зависимостей лучше использовать показатель, предложенный Пирсоном, который называется корреляционным отношением. Он вычисляется как квадратный корень из отношения межгрупповой дисперсии зависимой случайной величины к ее общей дисперсии. В данном случае группы формируются в пределах интервалов вариационного ряда независимой переменной. Корреляционное отношение можно вычислить с помощью следующей формулы:

	k
	∑ fx,i	( yx,i − y)2
η = i =1		n Sy2	.	(28)
Стандартные ошибки коэффициента корреляции и корреляци-
онного отношения можно оценить с помощью выражений:
SR =	1− R2			(29)
	n −2
и
Sη =	1−η2			(30)
	n −2	.

По соотношению величины коэффициента корреляции и корреляционного отношения можно сделать вывод о характере связи: прямолинейна она или криволинейна. Чем значительнее корреляционное отношение превышает коэффициент корреляции, тем более криволи-

46

нейной является эта связь. Для оценки степени криволинейности связи вычисляют меру криволинейности как разницу между квадратами корреляционного отношения и коэффициента корреляции:

K = η2 − R2 .

(31)

Вычислим рассмотренные выше показатели связи для пары случайных величин – диаметры и высоты деревьев в древостое. Для того чтобы выполнить вычисления, составим вспомогательную табл. 18. Подставляя значения сумм из данной таблицы в формулы (27) и (28), получим

		k
	∑ fi (xi − x) ( yi		− y)					2158,21
R =	i =1					=				= 0,6387
		n Sx Sy					200 7,436 2,272
и
		k
η2 =		∑ fx,i ( yx,i − y)2			600,17
		i =1		=					= 0,5811,	или
		n Sy2			200 5,164
η = 0,5811 = 0,7623.

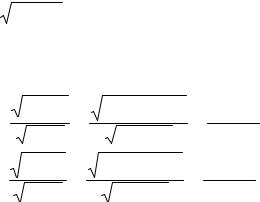
Теперь, пользуясь выражениями (29) и (30), вычислим стандартные ошибки коэффициента корреляции и корреляционного отношения:

SR =	1− R2	1−0,6387	2	0,7695	= 0,05469	;
	=	200 −2	=	14,07
	n −2
Sη =	1−η2	1−0,76232		0,6472	= 0,04600 .
	=	200 −2	=	14,07
	n −2

Полученные результаты говорят о том, что между диаметрами и высотами деревьев в древостое существует связь, а тот факт, что корреляционное отношение значительно превышает коэффициент корреляции, показывает нам, что эта зависимость скорее криволинейная, чем прямолинейная. Вычислим, пользуясь формулой (31), меру криволинейности для зависимости высот и диаметров:

K = η2 − R2 = 0,76232 −0,63872 = 0,5811−0,4079 = 0,1732.

47

48

Таблица 18. Вспомогательная таблица для вычисления коэффициента корреляции и корреляционного от-

ношения

H	D	17,65	20,85	24,05	27,25	30,45	33,65	36,85	40,05	43,25	46,45	49,65	52,85	56,05	Сумма	yi − y
	29,45				2										2	4,77
	28,45				1	3	1	2	1			1			9	3,77
	27,45			1		2	3	3	2	2	1	2	1		17	2,77
	26,45				1	3	5	8	5	3	2			2	29	1,77
	25,45			1	11	5	14	7	1	4		1			44	0,77
	24,45			6	7	11	8	2	1				1		36	–0,23
	23,45			3	10	6	1	1							21	–1,23
	22,45		1	13	5	2	1								22	–2,23
	21,45		3	2	2										7	–3,23
	20,45		5	1											6	–4,23
	19,45		2												2	–5,23
	18,45	1		1											2	–6,23
	17,45	2		1											3	–7,23
fx		3	11	29	39	32	33	23	10	9	3	4	2	2	200
yx		17,78	20,72	22,79	24,48	25,04	25,48	26,15	26,55	26,23	26,78	27,2	25,95	26,45
yx	− y	–6,9	–3,96	–1,89	–0,2	0,36	0,8	1,47	1,87	1,55	2,1	2,52	1,27	1,77
f x (yx − y)2		142,83	172,5	103,59	1,56	4,15	21,12	49,7	34,97	21,62	13,23	25,4	3,23	6,27	600,17
xi	− x	–13,95	–10,75	–7,55	–4,35	–1,15	2,05	5,25	8,45	11,65	14,85	18,05	21,25	24,45
f xy	(xi − x) ×
×( yi − y)		288,63	467,95	412,76	34,67	–13,39	54,14	176,98	158,02	162,28	93,7	181,94	53,98	86,55	2158,21

РЕГРЕССИОННЫЙ АНАЛИЗ

В предыдущем разделе было установлено, что между диаметрами и высотами деревьев существует связь. Наличие связи между случайными величинами, как правило, ставит перед исследователем следующую задачу – построение модели этой связи. Эта задача чаще всего решается с помощью регрессионного анализа. В данном случае наличие модели, позволяющей оценивать значения высот деревьев в древостое исходя из их диаметра, может оказать большую практическую пользу, так как трудоемкость измерения высоты растущего дерева значительно выше, чем трудоемкость измерения его диаметра.

Для построения регрессионного уравнения связи используют метод наименьших квадратов, позволяющий оценить коэффициенты уравнения заданного вида таким образом, чтобы сумма квадратов отклонений эмпирических значений зависимой переменной от теоретических значений была наименьшей.

Оценка коэффициентов прямой

Для того чтобы получить оценку коэффициентов b0 и b1 уравнения прямой линии методом наименьших квадратов, следует решить систему нормальных уравнений:

	n +b1	k	k	yi ,
b0		∑ fi xi	= ∑ fi
		i =1	i =1		(32)
	k	k		k
b0 ∑ fi xi +b1 ∑ fi xi2				= ∑ fi yi xi .
	i =1	i =1		i =1

Рассмотрим процесс вычисления коэффициентов уравнения прямой, моделирующей зависимость между высотами и диаметрами. Для этого на основе корреляционной решетки (табл. 6) составим вспомогательную таблицу для вычисления всех необходимых сумм (табл. 19). В данной таблице суммы вычисляются сначала по интервалам, а затем складываются. Подставив значения сумм в систему нор-

мальных уравнений (32), получим
b	200 +b	6320,8 = 4936,3,	(33)
0	1
b0	6320,8 +b1 210797,2 =158145,7.
		49