из них должны производиться новые виды продукции — по одному виду на одно предприятие.

Даны издержки производства единицы продукции, усл. ед.:

		Предприятия
	20	23	38	15	35
Вид продукции	8	29	6	35	35	.
	5	8	3	4	7

Издержки сбыта единицы продукции, усл. ед.:

	20	50	20	10	13
	7	90	8	35	60	.
	5	5	4	15	6

		Таблица 18
Вид продукции	Плановый объем	Себестоимость,
	производства, шт.	усл. ед.
1	35000	55
2	160000	50
3	54000	30

Закрепить выпуск продукции между предприятиями, обеспечивающий получение наибольшей прибыли за год.

1.22. В мастерской имеется два станка с соответствующими мощностями 60 и 70 станко-ч, на которых изготавливается три вида изделий. Стоимость изготовления единицы 1, 2, 3-го изделия на станке № 1 составляет соответственно 4, 6, 3 ден. ед., на станке № 2 − 5, 4, 2 ден. ед. Также известна производительность (шт./ч) каждого из двух станков при производстве 1, 2, 3-го изделий: для станка № 1: 8, 4, 2 соответственно; для станка № 2: 4, 2, 1 соответственно. Известно плановое задание по трем видам изделий: 160, 100, 100. Найти такой план выпуска изделий, чтобы издержки были минимальными.

§ 2. Двойственность в линейном программировании

Каждой задаче линейного программирования можно определенным образом поставить в соответствие некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной.

21

Пусть дана общая задача линейного программирования (исходная задача):

z(x) = c1 x1 + c2 x2 +... + cn xn → max

при условиях

a11 x1

+ a12 x2

+... + a1n xn

≤b1 ,

a

x

+ a

22

x

2

+... + a

2n

x

n

≤b

2,

21 1

...............

ak1 x1 + ak 2 x2

+... + akn xn

≤bk ,

+1)2 x2 +... + a(k +1)n xn =bk +1 ,

a(k +1)1 x1 + a(k

................

am1 x1 + am2 x2 +... + amn xn =bm ,

x j ≥ 0 ( j =

, l ≤ n ),

1,l

где x j

произвольного знака при j =

.

l +1, n

Двойственная к ней задача имеет вид f ( y) = b1 y1 + b2 y2 +... +bm ym → min

при условиях

a11 y1 + a21 y2 +... + am1 ym ≥ c1 ,a12 y1 + a22 y2 +... + am2 ym ≥ c2 ,

...............

a1l y1 + a2l y2 +... + aml ym ≥ cl ,

a1(l+1) y1 + a2(l+1) y2 +... + am(l+1) ym = cl+1 ,

................

a1n y1 + a2n y2 +... + amn ym = cn , yi ≥ 0 (i =1, k , k ≤ m ),

где yi произвольного знака при j = k +1, m .

(2.1)

(2.2)

(2.3)

(2.4)

(2.5)

(2.6)

Задача (2.4) ― (2.6), двойственная к задаче (2.1) ― (2.3),

строится по следующим правилам:

1) упорядочивается запись исходной задачи, т. е. если целевая функция задачи максимизируется, то ограничения-неравенства должны быть вида ≤, если минимизируется, то вида ≥. Выполнение этих условий достигается умножением соответствующих ограничений

22

на -1;

2)если исходная задача является задачей максимизации, то двойственная будет задачей минимизации. При этом вектор, образованный из коэффициентов при неизвестных целевой функции исходной задачи, совпадает с вектором констант в правых частях ограничений двойственной задачи. Аналогично связаны между собой векторы, образованные из коэффициентов при неизвестных целевой функции двойственной задачи, и константы в правых частях ограничений исходной задачи;

3)каждой переменной yi двойственной задачи соответствует i -e

ограничение исходной задачи, и, наоборот, каждой переменной x j

прямой задачи соответствует j -e ограничение двойственной задачи; 4) матрица из коэффициентов при неизвестных двойственной задачи AT образуется транспонированием матрицы A = (aij )m×n ,

составленной из коэффициентов при неизвестных исходной задачи; 5) если на j -ю переменную исходной задачи наложено условие

неотрицательности, то j -e ограничение двойственной задачи будет неравенством, в противном случае j -e ограничение будет равенством; аналогично связаны между собой ограничения исходной задачи и переменные двойственной.

Так как двойственная задача по отношению к двойственной является исходной, то задачи (2.1) ― (2.3) и (2.4) ― (2.6) образуют пару взаимно двойственных задач.

Дадим экономическую интерпретацию пары двойственных задач. Рассмотрим задачу рационального использования ресурсов. Пусть предприятие располагает ресурсами b1 , b2 ,…, bm , которые могут

использоваться для выпуска n видов продукции. Пусть также известны стоимость единицы j -го вида продукции c j ( j =1, n ) и

норма потребления i -го ресурса (i =1, m ) на производство единицы j -й продукции — aij . Требуется определить объем производства

23

продукции каждого вида x j ( j =1, n ), максимизирующий суммарную стоимость:

z(x) = c1 x1 + c2 x2 +... + cn xn (2.7)

При этом расход ресурсов не должен превышать их наличия:

a	x	+... + a		x		≤ b ,	(2.8)
11	1		1n		n	1
			.............
			+... + amn xn ≤ bm .
am1 x1
Все неизвестные			по		своему экономическому		смыслу

	неотрицательны:			(2.9)
	x j ≥ 0 ( j =1, n ).

По исходным данным сформулируем другую экономическую задачу (двойственную).

Предположим, что некоторая организация может закупить все ресурсы, которыми располагает предприятие. Необходимо

определить оптимальные цены (оценки) yi (i =1, m ) на эти ресурсы

исходя из естественного условия, что покупающая организация стремится минимизировать общую оценку ресурсов. Следует, однако, учитывать и тот факт, что за ресурсы покупающая организация должна уплатить сумму, не меньшую той, которую может выручить предприятие при организации собственного производства продукции.

Математическая модель задачи имеет следующий вид

f ( y) = b1 y1 +... +bm ym → min									(2.10)
a	y	+... + a			y		≥ c	,	(2.11)
11	1		m1			m	1
		.............
		+... + amn ym ≥ cn ,
a1n y1
									(2.12)
	yi ≥ 0 (i =1, m ).

Здесь f — общая оценка ресурсов. Каждое j -е ограничение из

системы (2.11) представляет собой неравенство, левая часть которого равна оценке всех ресурсов, расходуемых на производство единицы j -го вида продукции, а правая — стоимости единицы этой

продукции.

Заметим, что задачи (2.7) ― (2.9) и (2.10) — (2.12) образуют

симметричную паpy взаимно двойственных задач.

24

Пример 2.1. Фирма выпускает три вида изделий, располагая при этом сырьем 4-х типов: А, Б, В, Г соответственно в количествах 18, 16, 8 и 6 т. Нормы затрат каждого типа сырья на единицу изделия первого вида составляют соответственно 1, 2, 1, 0, второго вида — 2, 1, 1, 1 и третьего вида — 1, 1, 0, 1. Прибыль от реализации единицы изделия первого вида равна 3 усл. ед., второго — 4 усл. ед., третьего — 2 усл. ед.

Требуется:

1)составить план производства трех видов, максимизирующих прибыль;

2)определить дефицитность сырья;

3)установить размеры максимальной прибыли при изменении сырья А на 6 т, Б — на –3 т, В — на 2 т, Г — на 2 т. Оценить раздельное влияние этих изменений и суммарное их влияние на прибыль;

4)оценить целесообразность введения в план производства фирмы нового вида изделий (четвертого), нормы затрат на единицу которого соответственно равны 1, 2, 2, 0, а прибыль составляет 15 усл. ед.

Решение. 1) Обозначим через X = (x1 , x2 , x3 ) план производства

изделий трех видов, тогда математическая модель задачи примет вид z(x) = 3x1 + 4x2 + 2x3 → max

при ограничениях

x1 + 2x2 + x3 ≤18,2x1 + x2 + x3 ≤16,x1 + x2 ≤ 8,

x2 + x3 ≤ 6,

x j ≥ 0 , j =1,3 .

Решаем задачу симплексным методом, при этом последняя таблица будет иметь вид

Таблица 19

	i	Базис	cБ	b =	A0	3	4	2	0	0	0	0
						A1	A2	A3	A4	A5	A6	A7
	1	A4	0	4		0	0	0	1	0	–1	–1
	2	A3	2	3		0	0	1	0	1 2	–1	1 2
	3	A1	3	5		1	0	0	0	1 2	0	−1 2
	4	A2	4	3		0	1	0	0	−1 2	1	1 2

25

∆ j

33

0

0

0

0

1 2

2

3 2

Из таблицы следует X =(5,3,3,4,0,0,0), при этом z(X ) = 33 усл. ед. Согласно теоремам двойственности, Y =(0,1/2,2,3/2,0,0,0), при этом f (Y ) = 33 усл. ед.

2) Наиболее дефицитным является сырье типа В, для которого двойственная оценка y3 = 2 . Менее дефицитным является сырье вида Б, для которого y2 =12. Совсем не дефицитным является сырье A

( y1 = 0 ).

Для определения интервала устойчивости оценок найдем обратную матрицу для матрицы коэффициентов при базисных переменных в оптимальном решении системы ограничений. Базисными переменными в оптимальном решении являются x1 , x2 , x3 , x4 .

Матрица коэффициентов при этих переменных в системе ограничений имеет вид

		1	2	1	1
		2	1	1	0
	A = (aij ) =	1	1	0	0	.
		0	1	1	0

Тогда обратная матрица для матрицы A следующая:

			0	1 2	0	−1 2
−1			0	−1 2 1		1 2
A	= (dij ) =		0	1 2	−1	1 2		(находится в последней
			1	0	−1	−1

симплекс таблице в столбцах A4 , A5 , A6 , A7 ).

Найдем интервал устойчивости оценок по видам сырья:

						3
∆b1H = min	x j				=			= 6 ― нижний предел уменьшения,
						1 2
j(d1 j >0)	d
			1 j

							4
∆b1B = max	x j				=					= 8 ― верхний предел увеличения.
						−1 2
j(d1 j <0)	d
			1 j
Интервал устойчивости оценок по отношению к первому
ограничению
(b −bH ;b +bB )= (18 −6;18 +8) = (12;26) .
	1		1			1	1

26

Аналогично определим интервалы устойчивости оценок по отношению к ограничениям остальных видов сырья:

4

3

∆b2H =

min

3

;

=3, ∆b2B =

= 6 ,

−1 2

j(d2 j >0) 1

1 2

4

3

∆b3H =

min

3

;

= 6 ,

∆b2B =

= 3 ,

1 2

−1

j(d3 j >0) 1 2

5

3

4

∆b4H =

=5, ∆b4B

=

max

;

= 3 .

1

−1

j(d4 j <0)

−1

Интервалы устойчивости оценок по отношению: ко второму ограничению (16-3;16+6) =(13; 22),

ктретьему ограничению (8-6;8+3) =(2;11),

кчетвертому ограничению (6-5;6+3)=(1;9).

3)Изменения сырья согласно условиям задачи на +6, –3, +2, +2 т приводят к ограничению запаса сырья до 18+6=24, 16–3=13, 8+2=10, 6+2=8 т соответственно. Поскольку эти изменения находятся в пределах устойчивости оценок, на что указывают интервалы, то раздельное их влияние на прибыль определяется по формуле

				z		= y		b (i =		),
					i				1,4
							i	i
тогда
(z	max	)	1	= y			b = 0 6 = 0 ,
						1		1
(zmax )2				= y2 b2 =1 2 (−3) = −3 2 ,
(z	max	)	3	= y			b = 2 2 = 4 ,
						3		3
(zmax )4				= y4 b4 =3 2 2 =3 .
Суммарное влияние на прибыль:

zmax = (zmax )1 + (zmax )2 + (zmax )3 + (zmax )4 = 0 −32 + 4 +3 =11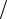2 усл. ед.

Если изменение сырья не находится в пределах устойчивости оценок, то необходимо найти новые условные оценки, т.е. решить задачу симплексным методом с изменением количества сырья соответствующих видов.

4) Для оценки целесообразности введения в план производства фирмы четвертого вида изделий используем формулу

27