26

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

НОВГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ ЯРОСЛАВА МУДРОГО

Институт электронных и информационных систем

Кафедра физики твердого тела и микроэлектроники

ИЗУЧЕНИЕ АВТОЭМИССИОННОГО МИКРОСКОПА

Методические указания

ВЕЛИКИЙ НОВГОРОД

2007

1 Цель работы

Знакомство с устройством и принципом действия автоэмиссионного мик­роскопа.

2 Основные сведения

Автоэлектронная эмиссия (АЭ) (полевая эмиссия, электростатическая эмиссия, туннельная эмиссия) – испускание электронов проводящими твердыми и жидкими телами под действием внешнего электрического поля Едостаточно высокой напряженности (~ 10⁷В/см). Автоэлектронная эмиссия обна­ружена в 1897 г. Р.У. Вудом. В 1929 г. Р.Э. Миликен и Ч.К. Лоритсен установи­ли линейную зависимость логарифма плотности токеавтоэлектронной эмис­сии отвида:lgj = f(1/E).В 1928 – 1929 г. г. Р. Фаулером и Л. Нордгеймом дано теоретическое объяснение автоэлектронной эмиссии на основе туннельно­го эффекта.

2.1 Потенциальный барьер на границе твердое тело – вакуум

Прозрачность потенциального барьера произвольной формы вычисляется с помощью метода Вентцеля-Крамерса-Бриллюэна [6]. Рассмотрим более про­стой случай – прохождение частицы сквозь потенциальный барьер прямоуголь­ной формы [7]. (Смотри рисунок 1).

Рисунок 1 – Потенциальный барьер прямоугольной формы

Барьер выделяет в пространстве три области:

Ι;

ΙΙ ;

ΙΙΙ;

В зависимости от потенциальной энергии частицы и высоты барьера следует различать:

а) низкие и

б) высокие барьеры.

Высокий барьер достаточной ширины непрозрачен дня частиц. Однако, узкий барьер, ширина которого соизмерима с областью неполного затухания волновой функции, становится прозрачным: Как будет показано ниже коэффициент прозрачности быстро возрастает с уменьшением ширины и высоты барьера.

Движение электрона представляется плоской волной Де-Бройля. На гра­нице двух областей, где происходит резкое изменение потенциала, эта волна должна вести себя так, как ведет себя световая волна на границе 2-х областей с различными показателями преломления. Это значит, что на границах областей IиII,IIиIIIволна Де-Бройля частично отражается, а частично проходит в об­ластьIIиIIIсоответственно. Т.е., переходя из одной области в другую, элек­трон имеет определенную вероятность отразиться и определенную вероятность пройти дальше.

Напишем стационарное уравнение Шредингера для каждой из областей в отдельности:

для Iобласти

для IIобласти (1)

для IIIобласти

где – волновые функции частицы в областяхI,II,III, а волновые числа частицы соответственно равны для областейIиIII.

(2)

где , для областиII

(3)

где .

В IиIIIобластях волновые функции представляют бегущие волны. В областиII.

Решение уравнения (1) будем искать в виде волн Де-Бройля

(4)

(5)

(6)

где и – соответственно падающие и отраженные волны от пер­вой стенки областиI;

и – падающая и отраженная волны Де-Бройля от второй стенки.

В области IIIсуществовать будет только проходящая волна , т.е. в дальнейшем для прохождения волны препятствий нет, т.е..

Так как функция должна быть непрерывна во всем пространстве надо, чтобы на границе областей функциии,ибыли равны друг другу (7), а также их первые производные при(8).

. (7)

. (8)

Подставив в равенства (7) и (8) значения функций ,ии их производные, получим следующую систему уравнений относительно коэффициен­тов.

, (9)

, (10)

(11)

(12)

Решая эту систему, найдем отношение . Для этого разделим уравне­ние (12) на, получим:

(13)

К полученному уравнению (13) прибавим уравнение (11)

(14)

Из уравнений (11) вычтем (13), получим:

(15)

Разделим уравнение (10) на , получим:

(16)

К уравнению (16) прибавим уравнение (9), получим:

(17)

Из уравнений (14) и (15) выразим коэффициентыиподставим в уравнение (17), получим:

(18)

Из (18) найдем отношение :

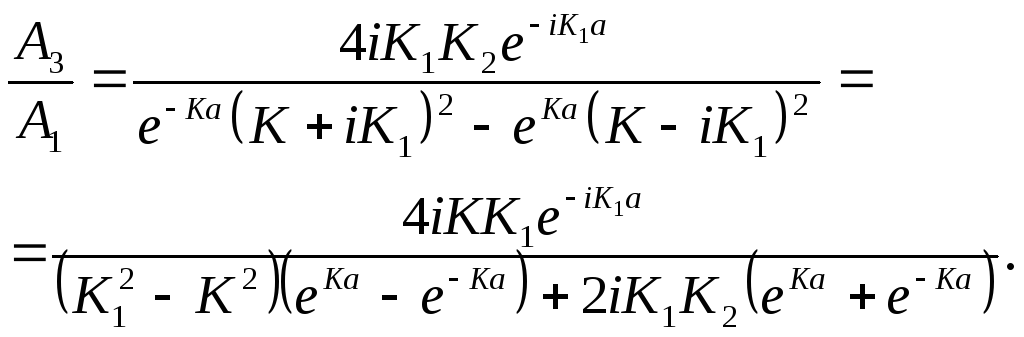(19)

После введения гиперболических функций (20) и (21)

(20)

(21)

получим

(22)

Амплитуда плоской волны оказывается отличной от нуля в области за барьером, хотя энергия частицы меньше высоты потенциального барьера . Это означает, что микрочастица с известной вероятностью может пройти через потенциальный барьер путем туннельного перехода.

Определим коэффициенты прозрачности (прохождения) частицы через барьер. Коэффициент прозрачности равен отношению плотности потока про­шедших барьер частиц к плотности потока падающих на барьер частиц. Пред­ставим себе цилиндр с основанием, равнымS = 1 см², и высотой, равной скоро­сти частиц. Если плотность частиц в этом цилиндре равна, то полное число частиц в нем будет. Число частиц, прошедших черезS= 1 см²в 1 секун­ду будет численно разно. Тогда коэффициент прозрачности будет равен:

(23)

Но плотность частиц пропорциональна квадрату амплитуды волны Де-Бройля, а отношение скоростей равно:

(24)

Так как , а, то

(25)

Поэтому коэффициент прозрачности окончательно выразится (26)

(26)

Длина волны Де-Бройля в области IиIIIона и та же, то, следовательно,

(27)

Подставляя (22) в (27), получим:

(28)

Так как , то

(29)

При достаточно больших х

Перепишем Dв виде

(30)

Число 4 в знаменателе мало по сравнению с , аи– величины одного порядка. Следовательно,D~, тогда прозрачность потенциального барьера можно записать

(31)

Из формулы (31) видно, что коэффициент прозрачности быстро убывает с увеличением ширины потенциального барьера "а" и высоты барьераотносительно энергии частицы. Подчеркнем, что энергия частицы после прохож­дения барьера равна ее первоначальной энергии (рисунок 2). Это означает, туннелирование частицы сквозь потенциальный барьер происходит без затраты энергии.

Рисунок 2 – Туннельный эффект при прохождении частицы потенциального барьера произвольной формы

Формула (31) рассчитана для барьера прямоугольной формы. При расчете коэффициента прозрачности потенциального барьера произвольной формы (ри­сунок 2) отрезок x₁x₂разбивается на ряд малых отрезков величиной, в каж­дом из которых потенциальная энергия меняется мало. Каждый из таких отрез­ков можно рассматривать как прямоугольный барьер и оценить вероятность прохождения его по формуле

(32)

По теореме умножения вероятностей вероятность совмещения независи­мых событий равна произведению вероятностей. Поэтому прозрачность потен­циального барьера описывается формулой (33)

(33)

2.2 Краткая теория автоэлектронной эмиссии металлов

Теория Фаулера-Нордгейма основывается на следующих физических предпосылках и методах расчета:

1 Задача ставится как одномерная (иными словами поверхность раздела металл-вакуум считается идеальной плоскостью), потенциальная энергия зависит только от координатых. Соответственно внешнее поле оказывается однородным.

2 Внутри металла энергия электрона на данном энергетическом уровне . Вне металла потенциальный порог обусловлен действием поляризационных сил (сил зеркального изображения), гдее– заряд электрона.

3 Прозрачность барьера D(Е) (33) вычисляется с помощью метода Вентцеля, Крамерса и Бриллюэна [8].

4 В качестве модели металла выбрана зоммерфельдовская модель сво­бодных электронов в потенциальном ящике, образующих вырожденный газ, подчиняющийся статистике Ферми-Дирона (рисунок 3).

5 Теория построена для температуры Т = 0 К.

Для определения плотности тока автоэмиссии необходимо просуммиро­вать потоки электронов, падающие на границу металл-вакуум, по всем возмож­ным энергиям электронов:

(34)

где f– функция Ферми распределения электронов по импульсам

– коэффициент прозрачности барьера при наличии внешнего электрического поляFу поверхности металла для электронов, падающих на металл с импульсомпо нормали к поверхности, совпадающей с осьюx.

– потенциальная энергия электрона, обусловленная взаимодействием со своим зеркальным изображением;

– потенциальная энергия электрона во внешнем поле;

– уровень Ферми в металле;

– работа выхода электрона;

– потенциальная энергия электрона, отсчитываемая от дна зоны проводимости

Рисунок 3 – Зависимость потенциальной энергии электрона у поверхности металла в зависимости от расстояния

Если , как этот принято, зависит только от, то интегрирование (34) поисводит рассматриваемую задачу к одномерной и при переходе от переменнойкдает:

(35)

где – число электронов с энергией междуипадающих изнутри металла на единицу поверхности в секунду, т.е. плотность потока электронов, падающих на единицу площади поверхности.

При наложении электрического поля напряженностью F потенциальная энергияописывает вне металла барьер(рисунок 3), прозрачность которого по (33) составляет

(36)

где е– заряд электрона;

– масса покоя свободного электрона;

–энергия электрона, отсчитываемая от дна зоны проводимости до уровня, с которого он туннелирует в вакуум;

– табулированная функция Нордгейма аргумента

(37)

В результате расчетов, детали которых описаны в [1], плотность тока вы­разится формулой

(38)

После подстановки значений констант для (работа выхода) в эВ,Ев В/см, в А/см²получим

(39)

где

(40)

(41)

Функции (40) и (41) задаются в виде таблиц. Функция , которая стоит в предэкспоненциальном множителе, близка к единице и слабо изменяется с измене­нием аргумента. Часто с полным основанием ее полагают равной единице. Функция Нордгеймасильно меняется при изменении, т.е. с изменением, и стоит в показателе экспоненты.

Для большинства обычных условий опыта функция лежит в пределах. Напряженность поляповерхности автокатода связана с при­ложенным напряжением соотношением

(42)

где – фактор поле. Плотность тока с силой тока связана соотношением

(43)

где – площадь экспонирующей поверхности.

Теперь, уравнение Фаулера-Нордгейма можно свести к форме, допускающей экспериментальную проверку

(44)

где

Поделив левую и правую часть уравнения (44) на и логарифмируя, найдем

(45)

Получили, что для данного острий из металла с работой выхода и радиусазависимость

(46)

представляет прямую линию. Ордината пересечения этой прямой с осью выражается первым членом, а тангенс угла наклона прямой

(47)

Зависимости (46), снятые экспериментально в определенном интервале напряжений , действительно представляют собой прямые линии, что под­тверждает правильность теоретической формулы.

Выражение (45) может быть использовано для определения работы выхо­да электронов металлических и в некоторых случаях полупроводниковых авто-катодов. Если известен радиус закругления острия , то по наклону прямойили по ординате пересечения ее с осьювычисляют работу выхода электронов.

Дня многих целей, в частности для определения работы выхода напыляемого адсорбата, вполне достаточно звание исходного напряженияи замены напряженностипо формуле, где, фактор поля, зависящей от геометрии острия (фактор поля). Уравнение (44) можно переписать в виде:

(48)

пригодным для практического применения при условии . Геометрия острия и, стало, быть, фактор поля, не изменяется при напылении на острие нескольких монослоев адсорбата при условии, что на поверхности адсорбента (подложки) не образуются трехмерные образования (наросты).

Например, снимается сначала зависимость с чистого вольфрама и строится вольтамперная характеристика

(49)

Затем производится напыление адсорбата (Ва,Сsиди какой-либо другой металл) и вновь снимается зависимость (49). При достижении монослойного покрытия автоэмиссионный ток будет определяться не свойствами подложки, а свойствами адсорбата. Зная работу выхода чистого вольфрама (4.5 эВ) или дру­гой подложки (Мо, Gе, Si и т.д.), можно определить работу выхода напыляемо­го адсорбата по формуле

(50)

Вместо уравнения (49) можно пользоваться соотношением

(51)

где и – анодное напряжения при неизменном автоэмиссионном токе.