Course_manual

КУРСОВАЯ РАБОТА «Практикум на ЭВМ: Структуры данных и алгоритмы»

семестр 2

Тематика курсовой работы связана с решением задач на дискретных конечных математических структурах. Задания предполагают использование:

-абстрактных структур данных (списки, стеки, очереди, деревья, графы, таблицы),

-алгоритмов поиска (линейный поиск, бинарный поиск, исчерпывающий поиск),

-алгоритмов обхода иерархических структур в ширину, в глубину,

-алгоритмов, оперирующих со структурами типа граф,

-алгоритмов порождения элементов конечного (как правило,

чрезвычайно большого) множества, которые удовлетворяют определенным ограничениям.

Задания на курсовую работу разбиты по темам: графы, системы дорог, деревья, языки, грамматики, логические формулы, выражения, игры.

Методические указания к выполнению курсовой работы (КР)

I.Требования к выполнению курсовой работы 1. Решая задачу необходимо:

–сделать формальную (на языке математики) постановку задачи

–продумать и обосновать метод решения задачи;

–продумать и обосновать формы представления (внешнего и внутреннего) исходных данных и результатов задачи, т.е. спецификации данных;

–реализуя решение, использовать принципы структурного и модульного

программирования.

2.Отчет по КР включает следующие разделы:

1.Условие задачи

2.Анализ задачи

3.Структуры данных, используемые для представления исходных данных и результатов задачи

4.Укрупненный алгоритм решения задачи

5.Структура программы

6.Текст программы на языке С

7.Набор тестов (в форме, соответствующей предметной области задачи)

8.Результаты работы программы

Анализ задачи

Данный пункт включает:

–определение исходных данных и результатов решения задачи;

–установление основных отношений (в виде математических формул, зависимостей и т.п.) между входными и выходными данными задачи;

–выделение основных подзадач, которые надо решить, чтобы достичь результата;

–выбор и описание метода ее решения. Метод решения должен быть описан на языке математики и предметной области задачи.

Структуры данных

В данном пункте определяются и описываются формы представления (внешнего и внутреннего) исходных данных и результатов задачи.

Алгоритм решения задачи

Степень детализации при описании алгоритма определяется так, чтобы было ясно какие действия надо выполнять, реализуя выбранный метод решения, и в чем заключаются основные проблемы данной задачи. Алгоритм может быть описан на языке блок-схем или псевдоязыке (псевдоСи).

Структура программы

В данном пункте описываются составные части программы (т.е. функции, реализующие отдельные действия алгоритма) и их взаимосвязь. Описание функции включает: назначение функции, прототип функции, назначение и описание параметров функции (описание параметра включает имя и назначение параметра, тип параметра).

Взаимосвязь функций можно представить в виде схемы, отображающей связь между функциями по управлению.

Набор тестов

Набор тестов должен быть необходимым и достаточным, включающим частные и особые случаи решения. Необходимо наглядное представление теста (например, графическое).

Оформление отчета

1.Отчет оформляется на стандартных листах бумаги формата А4 (297×210 мм) или листах школьной тетради, желательно в напечатанном виде. Записи ведутся только на одной стороне листа.

2.Титульный лист оформляется по образцу, приведенному на рис.1.

Министерство образования и науки Российской Федерации НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ

Курсовая работа по практикуму на ЭВМ: структуры данных и алгоритмы

Факультет	прикладной математики и информатики
Группа	ПМ-51
Студент	Иванов А.А.
Преподаватель	Петров В.В.
	Новосибирск 2006

II. Основные понятия

Математические модели большого числа задач могут быть описаны в терминах теории графов, поэтому алгоритмы исследования структуры (обработки) графов, а также способы их представления очень важны.

2.1. Некоторые основные определения

Графом (неориентированным графом) G(V,E) называется совокупность двух множеств, где V – конечное непустое множество элементов, называемых вершинами, а E – множество неупорядоченных пар различных элементов множества V (эти пары называются ребрами). Граф, состоящий из одной вершины, называется тривиальным.

Говорят, что ребро e = (u, v) соединяет вершины u и v. Ребро e и вершина u (а также e и v) называются инцидентными, а вершины u и v смежными. Ребра инцидентные одной и той же вершине также называются смежными.

Степень вершины – это число ребер, инцидентных ей. Вершина графа, имеющая степень 0, называется изолированной, а имеющая степень 1 – висячей.

Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.

Если элементом множества E может быть пара одинаковых (не различных) элементов V, то такой элемент E называется петлей. Псевдографом называется граф, у которого наряду с кратными ребрами допускаются и петли, причем даже несколько петель при одной вершине.

Граф называется простым, если любая пара вершин соединена не более чем одним ребром и граф не имеет петель.

Маршрут (путь) – это чередующаяся последовательность

a = v0 , e1 , v1 , , e2 , . . . , vn-1, en , vn = b

вершин и ребер графа такая, что ei = (vi-1 , vi), 1 ≤ i ≤ n. Говорят, что маршрут соединяет вершины a и b – концы маршрута. В простом графе маршрут можно задать перечислением лишь его вершин a = v0 , v1 , . . . , vn = b или его

ребер e1 , e2 , . . . , en.

Маршрут называется цепью, если все его ребра различные. Маршрут называется замкнутым, если v0 = vn.

Замкнутая цепь называется циклом. Цепь называется простой, если не содержит одинаковых вершин. Простая замкнутая цепь называется простым

циклом.

Гамильтоновой цепью называется простая цепь, содержащая все вершины графа. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа.

Вершина u достижима из вершины v, если существует путь из v в u.

Длина пути v0 , v1 , . . . , vn равна числу его ребер, т.е. n.

Расстояние между двумя вершинами – это длина кратчайшего пути, соединяющего эти вершины.

Часть графа G(V,E) – это такой граф G'(V',E'), что V' V и E' E.

Подграфом графа G называется такая его часть G', которая вместе со всякой парой вершин u, v содержит и ребро (u, v), если оно есть в G.

Дополнением графа G называется граф G' с тем же множеством вершин, что и у G, причем две различные вершины смежны в G' тогда и только тогда, когда они несмежны в G. Ребра графов G и G' вместе образуют полный граф. Граф называется полным, если любые две его вершины смежны.

Два графа G1 и G2 изоморфны, если существует взаимно однозначное отображение множества вершин графа G1 на множество вершин графа G2, сохраняющее смежность.

Граф называется связным, если для любой пары вершин существует соединяющий их путь. Максимальный связный подграф несвязанного графа называется компонентой связности данного графа.

Если задана функция F: V→M, то множество M называется множеством пометок, а граф называется помеченным. Если задана функция F: E→M, т.е. ребрам графа приписаны веса, то граф называется взвешенным.

Ребро графа называется ориентированным, если существенен порядок расположения его концов. Граф, все ребра которого ориентированные,

называется ориентированным графом (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E – дугами. Дуга (u, v) ведет от вершины u к вершине v, Вершину v называют преемником вершины u, а u - предшественником вершины v. Понятия части орграфа, пути,

расстояния, простого и замкнутого пути, цикла определяются для орграфа так же, как и для графа, но с учетом ориентации дуг.

Источник орграфа – это вершина, от которой достижимы все остальные вершины. Сток орграфа – это вершина, достижимая со всех других вершин.

Деревом называется связный граф без циклов.

Корневое дерево – это связный орграф без циклов, удовлетворяющий условиям:

1)имеется единственная вершина, называемая корнем, в которую не входит ни одна дуга;

2)к каждой некорневой вершине ведет ровно одна дуга.

Вершины, из которых не выходит ни одна дуга, называются листьями.

2.2. Представление графов в ЭВМ

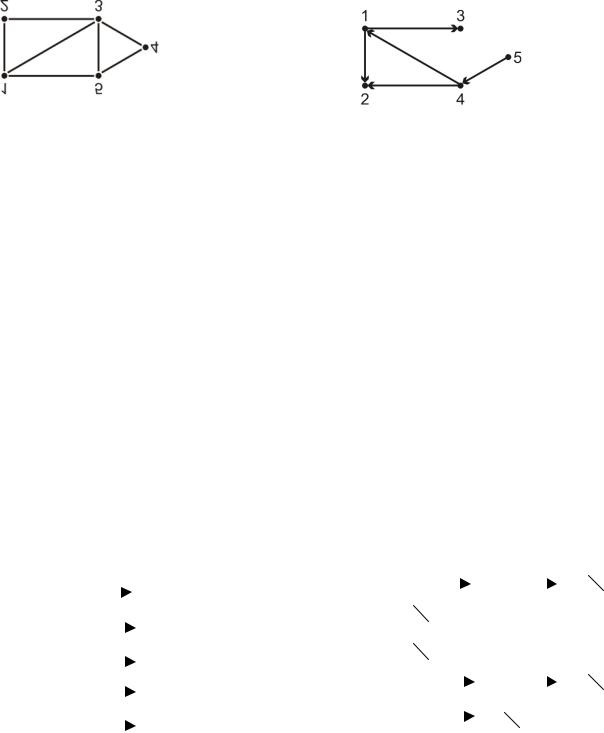
Представление в программе объектов математической модели – это важная составляющая программирования. Выбор наилучшего представления определяется требованиями конкретной задачи. Известны различные способы представления графов в памяти компьютера. Они различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Следует заметить, что во многих задачах на графах выбор представления является решающим для эффективности алгоритмов. На рис. 1.1. для неориентированного (а, б, в, г) и ориентированного (д, е, ж, з) графов показаны различные представления: б, е – матрица смежности; в, ж – матрица инцидентности; г – список смежности неориентированного графа при смежном размещении элементов списка (а); з – список смежности ориентированного графа при связанном размещении элементов списка (д).

2.2.1. Матрица смежности

Матрицей смежности помеченного графа с n вершинами называется матрица

A=[ aij], i, j = 1,2, . . . , n, в которой

1, если вершина i смежна с вершиной j, aij = 0, если вершина i не смежна с вершиной j.

Матрица смежности однозначно определяет граф (см. рис. 1.1. а–в, д–е). Для неориентированного графа матрица A является симметричной относительно главной диагонали. Число единиц в строке равно степени соответствующей вершины. Петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1.

Преимуществом такого представления является “прямой доступ” к ребрам графа, т.е. имеется возможность за один шаг получить ответ на вопрос “существует ли в графе ребро (x, y)?”. Для небольших графов, когда места в памяти достаточно с матрицей смежности часто проще работать. Недостаток заключается в том, что независимо от числа ребер объем занимаемой памяти составляет n× n или n× n/2- n, если использовать симметрию и хранить только треугольную подматрицу матрицы смежности. Кроме того, каждый элемент матрицы достаточно представить одним двоичным разрядом.

2.2.2. Матрица инцидентности

Матрицей инцидентности называется матрица B = [bij ], i =1, 2, . . . , n, j = 1,2, . .

. , m (где n – число вершин, а m – число ребер графа), строки которой соответствуют вершинам, а столбцы – ребрам. Элемент матрицы в неориентированном графе равен:

1, если вершина i инцидентна ребру j, bij = 0, если вершина i неинцидентна ребру j.

В случае ориентированного графа с n вершинами и m дугами элемент матрицы инцидентности равен:

	1,	если дуга j выходит из вершины i,
b = −1,		если дуга j входит в вершину i,
ij		если вершина i не инцидентна ребру j.
	0,

Строки матрицы также соответствуют вершинам, а столбцы – дугам.

Матрица инцидентности однозначно определяет структуру графа (см. рис. 1.1. а–в, д–ж). В каждом столбце матрицы B ровно две единицы. Равных столбцов нет.

Недостаток данного представления состоит в том, что требуется n× m единиц памяти, большинство из которых будет занято нулями. Не всегда удобен доступ к информации. Например, для ответа на вопросы “есть ли в графе дуга (x, y)?” или “к каким вершинам ведут ребра из вершины x?” может потребоваться перебор всех столбцов матрицы.

2.2.3. Матрица весов

Простой взвешенный граф может быть представлен своей матрицей весов W =[wij], где wij – вес ребра, соединяющего вершины i, j = 1,2, ... , m. Веса несуществующих ребер полагаются равными ∞ или 0 в зависимости от задачи. Матрица весов является простым обобщением матрицы смежности.

2.2.4. Список ребер графа

При описании графа списком его ребер (или, для орграфов списком дуг) каждое ребро представляется парой инцидентных ему вершин. Это представление можно реализовать двумя массивами (или одним двумерным)

x = (x0 , x1 , . . . , xm ) и y = (y0 , y1 , . . . , ym ),

где m –– количество ребер в графе. Каждый элемент в массиве есть метка вершины, а i–е ребро графа выходит из вершины xi и входит в вершину yi. Объем занимаемой памяти составляет в этом случае 2m единиц памяти. Неудобством является

большое число шагов, необходимое для получения множества вершин, к которым ведут ребра из данной вершины.

2.2.5. Списки смежных вершин графа

Граф может быть однозначно представлен структурой смежности своих вершин. Структура смежности состоит из списков Adj [x] вершин графа, смежных с вершиной x. Списки Adj [x] составляются для каждой вершины графа. Структура смежности может быть удобно реализована массивом из n (число вершин в графе) линейно связанных списков (см. 1.1. а–г). Каждый список

содержит вершины, смежные с вершиной, для которой составляется список. Список смежных вершин графа дает компактное представление для разреженных графов – тех, у которых множество ребер много меньше множества вершин. Недостаток этого представления таков: если мы хотим узнать, есть ли в графе ребро (x, y), приходится просматривать весь список Adj [x] в поисках y. Объем требуемой памяти составляет для ориентированных

(а)

	1	2	3	4	5
1	0	1	1	0	1
2	1	0	1	0	0
3	1	1	0	1	1
4	0	0	1	0	1
5	1	0	1	1	0

(б)

	½	1/3	1/5	2/3	3/4	3/5	4/5
1
	1	1	1	0	0	0	0
2	1	0	0	1	0	0	0
3	0	1	0	1	1	1	0
4	0	0	0	0	1	0	1
5	0	0	1	0	0	1	1

(в)

1
							2			3		5
2
								1		3
3
								1		2		4		5
4
								3		5
5
								1		3		4

(г)

Рис. 1.1.

(д)

	1	2	3	4	5
1	0	1	1	0	0
2	0	0	0	0	0
3	0	0	0	0	0
4	1	1	0	0	0
5	0	0	0	1	0

(е)

	½					1/3		4/1			4/2				5/4
1		1				1		-1			0				0
2		-1				0		0			-1				0
3		0				-1		0			0				0
4		0				0		1			1				-1
5		0				0		0			0				1
			(ж)
	1
									2						3
	2
	3
	4
									1						2
	5
									4
											(з)

n+ m и n+2m для неориентированных графов единиц памяти, где n – число вершин графа, а m – число ребер (дуг) графа. Если в основе алгоритма решения задачи лежат операции добавления и удаления вершин из списков, то хранение списков смежности удобно реализовать, используя связанное представление списков (см. 1.1. д–з).

2.3. Обход графа

Обход графа – это некоторое систематическое прохождение его вершин (и/или ребер). Обходя граф, мы двигаемся по ребрам (дугам) и проходим все вершины. При этом можно получить много информации, которая необходима для дальнейшей обработки графа, поэтому обход графа является основой многих алгоритмов исследования структуры графа. Если при посещении вершины структура графа не меняется, то наиболее полезными являются два основных способа обхода: обход в глубину и обход в ширину.

2.3.1. Обход (или поиск) в глубину

Пусть задан граф и фиксирована начальная вершина s (исходный граф может быть неориентированным или ориентированным). Стратегия поиска в глубину состоит в том, чтобы, начиная с начальной вершины, идти “вглубь”, пока это возможно (есть не пройденные исходящие ребра), и возвращаться и искать другой путь, когда таких ребер нет. Так делается, пока не обнаружены все вершины, достижимые из исходной. Если после этого остаются необнаруженные вершины, можно выбрать одну из них (как начальную вершину) и повторять процесс. Так делать до тех пор, пока мы не обнаружим все вершины графа.

Когда при поиске мы впервые обнаружим вершину v, смежную с вершиной u, необходимо отметить это событие. Алгоритм поиска в глубину использует для этого цвета (метки) вершин. Каждая из вершин вначале белая (не пройденная). Будучи обнаруженной, она становится серой. Когда вершина будет полностью обработана (т.е. когда список смежных с ней вершин будет просмотрен), она станет черной. Таким образом, в процессе поиска из графа выделяется часть – “дерево поиска в глубину” или несколько деревьев (лес поиска в глубину), если поиск повторяется из нескольких вершин. Каждая вершина попадает ровно в одно дерево поиска в глубину, так что эти деревья не пересекаются. Кроме этого можно ставить дополнительные метки на вершинах дерева: метку, когда вершина была обнаружена (сделалась серой) и метку, когда была закончена обработка списка смежных с u вершин (и u стала черной).

Приведенный ниже алгоритм использует представление графа списками смежных вершин Adj [u]. Для каждой вершины u графа дополнительно хранятся ее цвет Mark[u] и ее предшественник Pr[u]. Если предшественника нет (например, если u = s или u еще не обнаружена), то Pr[u ] = nil. Кроме того, в d [u] и f [u] записываются дополнительные для u метки: метки времени. В d [u] записывается время, когда вершина u была обнаружена (и стала серой), а в f [u] записывается время, когда была закончена обработка списка смежных с u вершин (и u стала

черной). В приводимом ниже алгоритме метки времени d [u] и f [u] это целые числа от 1 до 2 │V│; для любой вершины u выполнено неравенство: d [u] < f [u]. Вершина u будет белой до момента d [u], серой между d [u] и f [u] и черной после f [u] . Алгоритм использует рекурсию для просмотра всех смежных с u вершин.

Поиск_в_глубину (G)

1 {

2 for ( каждая вершина u V[G] )

3{ Mark [u]←БЕЛЫЙ;

4Pr [u] ←nil;

5}

6time ←0;

7for ( каждая вершина s V[G] )

8	if (Mark [s] = БЕЛЫЙ) Search (s);
9	}
	Search (u)
1	{

2Mark [u] ←СЕРЫЙ;

3 d [u] ←time←time+1;

4for (каждая v Adj [u])

5	{ if (Mark [v] = БЕЛЫЙ)
6	{ Pr [v] ←u; Search (v); }
7	}
8	Mark [u] ←ЧЕРНЫЙ;
9	f [u] ← time←time+1;
10	}

Алгоритм начинается с того, что сначала (строки 2–5) все вершины красятся в белый цвет (помечаются как не пройденные); в поле Pr помещается nil (пока у вершин нет предшественника). Затем (строка 6) устанавливается начальное (нулевое) время (переменная time – глобальная переменная). Для всех вершин (строки 7–8), которые все еще остались не пройденными (белыми), вызывается процедура Search. Эти вершины становятся корнями деревьев поиска в глубину.

В момент вызова Search (u) вершина u – белая. В процедуре Search она сразу же становится серой (строка 2). Время ее обнаружения (строка 3) заносится в d[u] (счетчик времени перед этим увеличился на единицу). Затем просматриваются (строки 4–7) смежные с u вершины; процедура Search вызывается для тех из них, которые оказываются белыми к моменту вызова. После просмотра всех смежных с u вершин саму вершину u делаем черной и записываем в f [u] время этого события.

2.3.2. Примеры решения задач методом поиска в глубину

Рассмотрим использование метода поиска в глубину на двух простых примерах.

Задача 1. Для неориентированного графа G(V,E) требуется найти ребра дерева поиска в глубину (древесные и обратные).

Для решения этой задачи достаточно пройти граф в глубину и сохранить информацию о пройденных ребрах дерева поиска в глубину и об обратных ребрах, если такие есть. Если граф не связен, то будем находить ребра всех деревьев поиска. Алгоритм решения этой задачи полностью соответствует общей схеме прохода в глубину. В качестве “серых” меток обнаруженных вершин будем использовать целые числа в диапазоне от 0 до │V│-1, это позволит просто различать обратные ребра. Считаем, что вершины графа помечены целыми числами от 0 до │V│-1. Граф задан структурой смежности Adj [u]. Ребра дерева поиска (и обратные ребра) запоминаются в массиве T, а в массиве B запоминается признак ребра: 1 – ребро дерева, 0 – обратное ребро.

Программа нахождения ребер дерева поиска в глубину (язык Си)

# include <stdio.h>

# define maxn 100 //максимальное число вершин в графе

# define maxADj 1000 // максимальная длина списка смежности графа

int nT, count;

int Adj [maxADj]; //список смежности графа

int Fst [maxn];	//указатели на списки смежности для каждой v V
int Nbr [maxn];	//число вершин в списке смежности для каждой v V
int Vt [maxn];	//список вершин графа
int Mark [maxn];	//метки вершин графа
int T [maxn];	//последовательность ребер при проходе в глубину
int B [maxn];	//признаки основных и обратных ребер при проходе
	//графа в глубину

//функция прохода графа в глубину и нахождения ребер дерева поиска void Depth ( int x, int s)

{
int i, v;
count ++;
Mark [x] = count;	// вершина x помечается как пройденная вершина
for (i = 0; i < Nbr[x]; i++)	//просмотр списка смежности вершины x
{ v = Adj [Fst [x] + i];	//выбор из списка смежности x еще не
if (Mark [v] = = -1)	//пройденной вершины
{ nT = nT +2; T [nT – 1] = x; T [nT] = v;
B [nT/2] = 1;	//установлен признак основного ребра
Depth (v, x);

}
else
if ( Mark [v] < Mark [x] && v != s )
{ nT = nT +2;	T [nT – 1] = x; T [nT] = v;
B [nT/2] = 0;	//установлен признак обратного ребра

}