7. Функции комплексного переменного / m7var21

Вариант 21

Задача 1. Вычислить значение функции (ответ дать в алгебраической форме):

	а) Arsh	i		б)
			;		4i − 3
	2

Решение. а). Будем вычислять Arsh(i/2) по формуле Arsh z) = Ln z + z2 + 1) . В данном

примере z=i/2, следовательно, Arsh	i	= Ln(	i	±	3	), так как	z2 = −	1	. Далее воспользуемся
2		2			2		4

формулой Ln z) = ln z + i(ϕ + 2kπ) . В данном случае у функции Ln(z) имеется два значения

z:			z		=					3		+			i					и					z		= −				3		+	i	. Найдём модули и аргументы этих чисел:
				1																						2
										2		2																			2	2
																									2		1				2												π											5π
																		3																																														3
	z	1	=			z		2			=					±										+						=1,			ϕ	= arg z					1	=			,			ϕ		2	= arg z	2	=		, так как cos					ϕ	1	=					> 0,	а
																		2									2								1								6											6										2
cosϕ								= −				3				< 0.Таким образом Arsh																							i	= Ln(						3		+		i	) = ln(1) + iπ 2k +					1	) = iπ 2k +					1	) и
					2
												2																								2									2					2					6							6
Arsh					i		= Ln(−													3		+			i	) = ln(1) + iπ 2k +											5	) = iπ 2k +									5		) . Учитывая, что 2k +									5	= 2k +1−						1	,
					2													2							2											6											6								6									6

формулы можно объединить: Arsh i = iπ k + (−1)k 1) .

26

б). Корни находятся по формуле

=

(cos ϕ + 2kπ + i sin ϕ + 2kπ) , где k=0, 1. При k=0

z

z

2

2

(cos ϕ + i sin ϕ) . Полагая k=1, получим второй корень

z

получим первый корень

z =

2

2

=

(cos(ϕ + π) + i sin(ϕ + π)) = −

(cos ϕ + i sin ϕ)

(по формулам приведения). В

z

z

z

2

2

2

2

3

4

= 5 и, следовательно, z = 5(−

+

i) .

данном примере z=-3+4i. Тогда

z

=

(−3)2 + 42

5

5

Поскольку z = z (cosϕ + i sin ϕ) , то в данном случае cosφ=-3/5, а sinφ=4/5. Учитывая, что

sin2 ϕ =			1			1− cosϕ) и cos2 ϕ =					1			1+ cosϕ) , получим:
		2	2							2	2
sin2 ϕ =	1	1+		3	) =		4	и cos2 ϕ =	1	1−		3		) =	1	. Отрицательное значение косинуса и
2	2		5			5		2	2		5			5

положительное значение синуса соответствуют второму координатному углу комплексной плоскости, так что π/2<φ<π. Поэтому, соответственно, π/4<φ/2<π/2. В таком

случае sin ϕ > 0, и									cos ϕ > 0 , т.е. sin ϕ =									2					и cos ϕ =				1			. Окончательно получаем
			2						2	2						5								2			5
							(cos ϕ + i sin ϕ) = ±					(		1							2
				z
	z = ±									5							+ i								) = ± 1+ 2i) .
						2			2	5											5
								i	= iπ k + (−1)k			1				б)
Ответ.			а) Arsh										) ;									4i			− 3 = ± 1+ 2i) .
			2							6

Задача 2. Выяснить геометрический смысл соотношения. Сделать чертёж. z − 2i − z + 2i = 2.

Решение. Так как z=x+iy, то данное соотношение имеет вид: x + i y − 2) − x + i y + 2) = 2.

Или 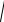x2 + y − 2)2 − 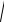x2 + y + 2)2 = 2 . Перенесём второй корень в правую часть равенства и возведём обе части в квадрат. Получим:

x2 + y2 − 4y + 4 = 4 + 4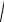x2 + y + 2)2 + x2 + y2 + 4y + 4 . Или 4x2 + y + 2)2 = − 4 + 8y) .

Отметим, что правая часть равенства не должна быть

yотрицательной, т.е. должно быть 4+8y<0, y<-1/2. Возведём x полученное равенство ещё раз в квадрат:

16x2 + 64x + 64 + 16y2 =16 + 64y + 64y2. Или 16x2 − 48y2 = −48.

Поделив всё равенство на правую часть, получим каноническое

уравнение гиперболы с фокусами на мнимой оси: y2 − x2 =1.

3

Ответ. Данное соотношение представляет уравнение нижней ветви гиперболы y2 − x2 =1( так как переменная y должна быть отрицательной).

				3
	Задача 3. Решить уравнение: e2z + 1− i = 0.
	Решение. Преобразуем уравнение: e2z = −1+ i																		или			z =	1	Ln(−1+ i) . Тогда
																						2
	z =	1		−1+ i				+ i(	3π	+ 2kπ)] =			1			+ 2k +	3	)πi] =		1	ln 2 + k +				3	)πi .
			[ln											[ln	2
	2							4		2					4				4					8
	Ответ.			z =	1	ln 2 + k +					3	)πi .
				4						8

Задача 4. Нет условия задачи.

Задача 5. Восстановить аналитическую функцию по заданной действительной части её:

Ref z) = u = Ax3 + 3xy2 − 3x2 y + y3 , если f(i)=1.

Решение. Чтобы функция u(x,y) бала действительной частью аналитической функции нужно, чтобы она была гармонической, т.е. её лапласиан ∆u был бы равен нулю: ∆u=0,

	≡	∂2		+	∂2
							. Проверим выполнение этого условия, для чего найдём производные
		∂x	2		∂y	2

второго порядка от u по x и по y:

∂u

= 3Ax

2 + 3y2 − 6xy,

∂2u

= 6Ax

− 6y,

∂u

= 6xy

− 3x2 + 3y2 ,

∂2u

= −6x

+ 6y.

∂x

∂x2

∂y

∂y2

Чтобы лапласиан ∆u был равен нулю, нужно положить A=-1. Таким образом, функция

u x, y) = −x3 + 3xy2 − 3x2 y + y3 является гармонической. Восстановим мнимую часть v(x,y)

функции f(z)=u(x,y)+iv(x,y), пользуясь условиями Даламбера-Эйлера:			∂u = ∂v ,		∂u = −	∂v	.
			∂x	∂y	∂y	∂x
Из первого условия получаем:	∂v =	∂u = −3x2 + 3y2 − 6xy. Тогда v x, y) = ∫		∂vdy + ϕ x) , или
	∂y	∂x		∂y

v x, y) = ∫(−3x2 + 3y2 − 6xy)dy + ϕ x) = −3x2 y + y3 − 3xy2 + ϕ x). Производная по x от этого

выражения равна ∂v = −6yx − 3y2 + ϕ′ x). С другой стороны по второму условию

∂x

Даламбера-Эйлера ∂v = −6xy + 3x2 − 3y2 . Приравнивая эти выражения, получим:

∂x

ϕ′ x) = 3x2 . Или ϕ x) = x3 + C. Таким образом, v x, y) = −3x2 y + y3 − 3xy2 + x3 + C. Тогда

f z) = −x3 + 3xy2 − 3x2 y + y3 + i (−3x2 y + y3 − 3xy2 + x3 + C). Перейдём к переменной z:

f z) = − x3 + 3ix2 y − 3xy2 − iy3 ) + i x3 + 3ix2 y − 3xy2 − y3 ) + iC = −z3 + iz3 + iC. . Воспользуемся дополнительным условием f(i)=1. В данном случае f(i)=i+1+iC. Следовательно, C=-1.

Ответ. f z) = −x3 + 3xy2 − 3x2 y + y3 + i (−3x2 y + y3 − 3xy2 + x3 −1) = z3 i −1) − i.

Задача 6. Вычислить интеграл по дуге C от точки z1 до точки z2.

∫ i − 2z)dz;			C − прямая, z1 = 0, z2 = 2 + 4i.
C

Решение. Вычислим интеграл, сводя его к криволинейным интегралам второго рода по формуле ∫f z)dz = ∫udx − vdy + i∫udy + vdx . В данном случае f(z)=(i-2x+2iy), т.е. u=-2x,

C	C			C
v=1+2y. Значит ∫
	i − 2z)dz = ∫(−2x)dx − 1+ 2y)dy + i∫(−2x)dy + 1+ 2y)dx . Примем x за
C			C	C

параметр. Составим уравнение прямой, проходящей через две точки:

y = x , т.е. y = 2x, dy = 2dx . Начальной точке z1=0 соответствует значение x=0, конечной

42

z2=2+4i – значение x=2. Следовательно,

2

2

10x

2

2

02 = −24 + 2i .

∫ i − 2z)dz = ∫(−2x − 2 − 8x)dx + i∫(−4x +1+ 4x)dx= [−

− 2x]

+ ix

2

C

0

0

0

Ответ.

∫ i − 2z)dz = − 24 + 2i .

C

i

Задача 7. Вычислить интеграл от аналитической функции. ∫ez

z −1)dz .

1

Решение. Применим формулу интегрирования по частям:

i

u = z −1

du = dz

i

i

i

∫ez z −1)dz =

=

z −1)ez

− ∫ez dz = i −1)ei − ez

= i −1)ei − ei + e1 =

= e

z

= e

z

dv

dz

v

1

1

1

1

= e + iei − 2ei = e + i − 2)ei = e + i −2)[cos1+ isin1] = e −2cos1 − sin1+ i(cos1− 2sin1) .

i

Ответ.

∫ez z −1)dz = e −2cos1− sin1+ i(cos1− 2sin1)

1

Задача 8. Найти интеграл, используя интегральную формулу Коши, по конту-

рам L1, L2, L3.

L∫

eπzdz

,

1)

L1 :

z −1− i

=

1

, 2) L2

: x2 +

4y2

=1, 3)

L3 :

z −1− i

=

3

.

z + i)2 z − i)

2

9

2

y

Решение. 1). Подынтегральная функция аналитична

всюду, за исключением точек z=-i и z=i. В круге

L3

z −1− i

≤

1

подынтегральная функция аналитична.

L1

2

ez−idz

2

x

-1

Следовательно, I1 = ∫

2

= 0 . 2). В эллипсе

L

z

+1)(z + i)

1

x2 +

4y2

=1 есть две особые точки z=-i и z=i. Поэтому

L2

9

применим теорему Коши для многосвязной области:

I2 =

eπzdz

=

eπzdz

+

eπzdz

, где l1

L∫

z + i)2 z − i) l∫

z + i)2

z − i) l∫

z + i)2 z − i)

2

1

2

- окружность достаточно малого радиуса с центром в точке z=-i, а l2 - окружность малого радиуса с центром в точке z=i. Вычислим интегралы по интегральной формуле Коши:

∫

l1

eπzdz						eπz	dz
				= ∫		z − i
									=
z + i)	2	z	− i)			z + i)		2
				l
				1

2πi		d	e		πz		πeπz	z − i) − eπz		πi 2πi +1)
							= 2πi	z − i)2	= −		,
1! dz z					− i					2
						z=−i			z=−i

eπz

dz

∫

eπzdz

∫

z + i)2

eπz

πi

=

= 2πi

=

. Следовательно,

z + i)

2

z

− i)

2

2

l2

z − i)

l2

z + i)

z=i

I

=

ez−idz

= [−

πi 2πi +1)

+

πi

= π2

2

]

L∫2

z2 +1)(z

+ i)

2

2

3). Внутри области

z −1− i

≤

3

расположена одна особая точка z=i. Интеграл по контуру

2

L3 совпадает с уже вычисленным интегралом по контуру l2:

eπz

eπzdz

dz

eπz

= ∫

= ∫

z + i)2

=

πi

I3

= 2πi

z + i)

2

z − i)

z − i)

z + i)

2

2

L3

L3

z=i

Ответ.

I

1

= 0,

I

2

= π2 ,

I

3

= πi .

2

Задача 9. Разложить функцию в ряд Лорана в областях.

z +1

,

1) 2 <

z

< 5

2)

z

> 5.

z2 + 7z +10

Решение. Корнями уравнения z2+7z+10=0 являются числа z1=-5 и z2=-2. Разложим эту

дробь на простые дроби:		z + 1	=	A		+	B	=	A z + 2) + B z + 5)	. Или
		2 + 7z +10		z +			z + 2
	z				5				z + 5)(z + 2)

A z + 2) + B z + 5) = z +1. При z=-5 получим -3A=-4, т.е. А= 4/3. Если z=-2, то 3B=-1, т.е.

В=-1/3. Следовательно,

z + 1

=

4

1

−

1

1

. 1). В кольце 2 <

z

< 5 имеем

2

z

z

2 + 7z +10 3

z + 5 3

z + 2

<1 и

<1. Тогда дробь можно представить следующим образом:

z5

z +1

=

4

1

−

1

1

. Воспользуемся формулой для бесконечно убывающей

z2 + 7z +10

z

2

3

5 1

+

)

3

z 1+

)

5

z

геометрической прогрессии:

1

=1+ q + q2 + ... + qn + ..., где

q

<1. В первой дроби q=-z/5,

1− q

во второй дроби q=-2/z. Следовательно,

z + 1

4

∞

(−1)n zn

1

∞

(−1)n−1 2n−1

=

∑

−

∑

. 2). В кольце

z

> 5 выполняются

2

+ 7z +10

n+1

n

z

3 n=0 5

3 n=1

z

неравенства

2

<1

и

5

<1. Следовательно,

z

z

z + 1

4

1

1

1

1

∞

4 5

n−1

− 2

n−1

=

−

=

∑(−1)n−1

.

z2 + 7z +10

5

2

zn

3

z 1

+

)

3

z 1+

)

3

n=1

z

z

z + 1

4

∞

(−1)n zn

1

∞

(−1)n−1 2n−1

Ответ. 1).

=

∑

−

∑

. в кольце 2 <

z

< 5 .

z

2

+ 7z +10

3

n+1

3

z

n

n=0 5

n=1

z +1

1

∞

4

5

n

− 2

n−1

2).

=

∑(−1)n−1

в кольце

z

> 5 .

z2 + 7z +10 3 n=1

zn

Задачи 10-11. Вычислить интегралы с помощью вычетов.

10. ∫

2z +1

dz

11.

∫

z3ch

1

dz

3

+ 1

z

=5

z

− 27)z

z+1

=2

z

Решение. 10.

Корни знаменателя: z

= 0,

z

= 3(cos

2kπ

+ isin

2kπ

), z

= 3,

1

2,3,4

2

3

3

= −

3

1− i

= −

3

1+ i

z

3

3),

z

4

3) . Все корни являются простыми полюсами

2

2

подынтегральной функции. Тогда

Re s

2z +1

= lim [

z 2z +1)

] = lim [

2z +1

] = −

1

,

0

z

3 − 27)z

z→0

z3 − 27)z

z→0

z3 − 27)

27

Res

2z +1

= lim [

z − 3)(2z +1)

] = lim [

2z +1

] =

7

z3 − 27)z

z − 3)(z2 + 3z + 9)z

3

z→3

z→3 z2 + 3z + 9)z

81

3

2z + 1

[z +

1− i

3)](2z +1)

Res

=

lim

[

2

] =

z3 − 27)z

3

3

3

3

1+ i

−

1−i

3)

z→−

1−i

3)

z z − 3)[z +

1− i

3)][z +

3)]

2

2

2

2

2z +1)

] = − 2 + 3i

=

lim

[

3 ,

3

3

z z − 3)[z +

+ i

81

z→−

1−i 3)

1

3)]

2

2

3

2z +1

[z +

1+ i

3)](2z +1)

Res

=

lim

[

2

] =

z3 − 27)z

−

3

1+i

z→−

3

1+i

z z − 3)[z +

3

1− i

3)][z +

3

1+ i

3)

3)

3)]

2

2

2

2

2z +1)

− 2 − 3i

=

lim

[

] =

3

. Получим окончательно:

3

3

z z − 3)[z +

− i

81

z→−

1+i 3)

1

3)]

2

2

2z +1

4

1

7

+ − 2 + 3i 3 − 2 − 3i 3] = 0 .

dz = 2πi∑Resf z) =2πi[−

+

∫=5

z

z3 − 27)z

k=1

zk

27

81

81

11). Подынтегральная функция имеет существенно особую точку z=-1. Поэтому для вычисления вычета относительно этой точки следует разложить функцию в ряд Лорана. Воспользуемся разложением в ряд функции ch(w) по степеням w:

ch(w) =1+

w2

+

w4

+

w6

+ ... Полагая w =

1

, получим:

z +1

2!

4!

6!

z3ch

1

= z3 1+

1

+

1

+

1

+ ...) = z3 +

z3

+

z3

+ ...

z +1

2! z + 1)2

4! z +1)4

6! z + 1)6

2 z +1)2

24 z +1)4

Разложим, кроме того, функцию z3 по степеням (z+1):

z 3 =

z + 1 − 1)3

=

z + 1)3 − 3 z + 1) 2

+ 3 z + 1) − 1 . Тогда

z3ch

1

= [(z +1)3 − 3 z +1)2 + 3 z + 1) −1](1+

1

+

1

+

1

+ ...)

z +1

2! z +1)2

4! z +1)4

6! z +1)6

Последующие слагаемые не содержат степени (z+1)-1. Перемножая ряды, находим, что

коэффициентом при (z+1)-1 в разложении функции будет число 3 + 1 = 37 . Вычет данной

2! 4! 24

функции равен коэффициенту при (z+1)-1 в данном разложении, т.е. Res[z3ch												1	] =	37	.
												z +1
											−1		24
Следовательно. ∫				z3ch	1		dz = 2πi	37	=	37	πi .
					z +1
	z+1		=2				24		12

Ответ. 10.

∫

2z +1

dz = 0.

11.

∫

z3ch

1

dz =

37

πi .

3

+1

z

=5

z

− 27)z

z+1

=2

z

12

Задача 12. Вычислить несобственный интеграл с помощью вычетов.

∞

dx

∫

.

x

2

+ 1)(x

2

+

4)

2

−∞

Решение. Корнями знаменателя функции f

z) =

1

являются числа

z2 + 1)(z2 + 4)2

z1,2

= ±i, z3,4

= ±2i . В данном случае в верхней полуплоскости расположены два полюса

z=i и z=2i данной функции.

∞

dx

1

1

Тогда

∫

= 2πi(Res

+ Res

).

x

2

+ 1)(x

2

+

4)

2

z

2

+1)(z

2

+ 4)

2

2

+1)(z

2

+

4)

2

−∞

i

2i z

Res

1

= lim

z − i)

= lim

1

=

1

,

2

+1)(z2

+ 4)2

z + i)(z − i)(z2 + 4)2

z + i)(z2

+ 4)2

i

z

z→i

z→i

18i

Res

1

= lim

d

z − 2i)2

= lim

d

1

=

2 +1)(z2

+ 4)2

+ 2i)2

z − 2i)2

z2 +1)

z + 2i)

2

z2 +

2i

z

z→2i dz

z

z→2i dz

1)

= lim[−

2 z

+ 2i)(z2 +1) + 2z z +

2i)

2

] = lim[−

2 z2 +

1) + 2z z +

2i)

11

] = −

.

[(z + 2i)2

z2 +1)]2

32 9i

z→2i

z→2i

z + 2i)3 z2 + 1)2

∞

dx

2πi

11

5π

Следовательно. ∫

=

1−

) =

.

2

+1)(x

2

+ 4)

2

18i

16

−∞

x

144

∞

dx

5π

Ответ.

∫

=

.

2

+1)(x

2

+ 4)

2

−∞

x

144

Задача 13. Вычислить интеграл от заданной ветви многозначной функции по кривой С от точки z1 до точки z2.

	∫		dz
					, где С: верхняя половина окружности	z	=1, z1=1, z2=-1, 4 1 = i .
		4
			3
	C		z

Решение. Точки z1 и z2 не являются особыми точками для подинтегральной функции. Следовательно, можно применить формулу Ньютона-Лейбница:

dz

z2

ϕ + 2kπ

ϕ + 2kπ

= 44 z

= 4(4 z

− 4 z

) . Рассмотрим функцию 4

z = 4

+ isin

z

(cos

) .

∫ 4

2

1

z

3

z1

4

4

C

Рассматривается та ветвь функции, для которой в точке z=1 функция будет принимать

заданное значение. С одной стороны 41 = cos 2kπ + isin 2kπ . С другой стороны

4 4

48 = i = cos π + isin π . Сравнивая эти выражения, приходим к выводу, что указанной ветви

22

функции соответствует значение k=1. Следовательно, данная ветвь функции имеет

уравнение. 4

= 4

(cos ϕ + 2π + isin ϕ + 2π) . Таким образом,

= 4

= cos

2π

+ isin

2π

= i ,

z

z

4 z

1

1

4

4

4

4

= cos π + 2π

+ isin π + 2π

= −

1

+

i

. Следовательно,

4 z

2

= 4

−1

4

4

2

2

dz

z2

1

i

= 44 z

= 4(4 z

− 4 z

) = 4(−

+

− i) = −2 2

+ i 2 2

− 4) .

∫ 4

z1

2

1

3

2

2

z

C

Ответ. ∫			dz
						= −2 2 + i 2 2 − 4) .
	4
C			z	3