§ 40. Двойственность и планарность

Целью этого параграфа является получение еще од­ного критерия планарности графа, основанного на поня­тии двойственности.

Условимся, что всюду в этом параграфе слово «граф» означает «псевдограф». Кроме того, видоизменим здесь использованную выше (см. § 3) операцию стягивания ребра е = uv EG, под которой теперь будем понимать удаление ребра е и отождествление вершин и и v в но­вую вершину, инцидентную тем ребрам графа G, которые были инцидентны вершинам и и v, за исключением реб­ра е (рис. 40.1). Тем самым теперь появляющиеся при стягивании ребра кратные ребра не отождествляются, как ранее.

Для плоского графа G построим новый плоский граф G*, который назовем геометрически двойственным к G. Для этого внутри каждой грани Ti графа G выберем по одной точке V*i. Эти точки — вершины будущего графа G*. Далее, каждому ребру е  EG поставим в соответствие жорданову кривую е*, которая пересекает лишь одно реб­ро е графа G и соединяет вершины v *_i, лежащие в гранях, границы которых содержат ребро е (таких граней может быть две или одна). Кривые е* — ребра графа G*. Очевидно, что ребра графа G* можно провести так, чтобы они не пересекались. На рис. 40.2 сплошной линией изображен граф G, а пунктирной — граф G*. Заметим, что петлю в G* порождает всякий мост в G, а кратные

ребра появляются в G* тогда и только тогда, когда две грани графа G имеют более одного общего ребра.

Из этого построения очевидно, что граф G*, геометри­чески двойственный к плоскому графу G, определяется однозначно с точностью до изоморфизма, причем граф G*

всегда связен. Последнее утверждение легко доказать индукцией по числу вершин графа G* (т. е. по числу гра­ней графа G) путем стягивания ребра е* графа G*, что, очевидно, соответствует удалению ребра е в графе G. При этом, если ребро е — граница двух граней, то упомянутые операции приводят к уменьшению числа вершин графа G* (числа граней графа G) на единицу. Применяя формулу Эйлера, легко получить Утверждение 40.1. Если G — плоский связный (n, т)-граф с f гранями, a G* — (n*, т*)-граф, геометрисески двойственный к нему, с I* гранями, то n* = f, n* = m, f* = n.

Поскольку граф G* — плоский, то можно построить граф, геометрически двойственный к G*, который естественно обозначить через G**. Связь между графами G и G** устанавливает следующая теорема.

Теорема 40.2. Если G — плоский связный граф, то граф G** изоморфен графу G.

Из утверждения 40.1 следует, что n** —f* = n, где n**=\G**\. Следовательно, каждая грань графа G* со­держит одну вершину графа G (G**). Поэтому построе­ние, при помощи которого граф G* получен из G, можно обратить, т. е. получить G из G*.

Граф, двойственный к планарному графу, определяет­ся следующим образом: рассмотрим любую укладку это­го графа и построим геометрически двойственный граф. Здесь уместно отметить, что планарный граф, допускаю­щий несколько укладок на плоскости, может иметь не изоморфные двойственные графы (см. упр. 25).

Теорема 40.3. Пусть G —планарный граф, G* — граф, геометрически двойственный к G. Подмножество ребер из G образует простой цикл в G тогда и только тогда, когда соответствующее множество ребер из G* об­разует разрез в G*.

Для доказательства этой теоремы потребуется одна очевидная лемма.

Лемма 40.4. Пусть Н — связный граф, множество VH вершин которого разбито на два подмножества V₁ и V₂. Множество ребер

является разрезом тогда и только тогда, когда графы H(V₁) u H(V₂) связны.

Доказательство теоремы 40.3. Не исклю­чая общности, будем считать, что G — плоский граф.

Пусть С — простой цикл в G. Тогда он ограничивает одну или несколько внутренних граней графа G, т. е. ог­раничивает часть плоскости, содержащую непустое мно­жество W вершин графа G*. Поэтому ребра из G*, пере­секающие ребра цикла С, образуют множество М в G*, удаление которого разделяет связный граф G* на два подграфа с множествами вершин W и VG*\W (рис. 40.3). Индукцией по числу вершин легко доказать связность каждого из этих подграфов. Следовательно, на основании леммы 40.4 М — разрез в графе G*.

Путем обращения приведенного выше рассуждения до­казывается обратное утверждение о том, что разрезу в G* соответствует простой цикл в G.

Теорема 40.3 естественным образом приводит к следующему комбинаторному определению двойственности графов, которое обобщает геометрическую двойственность позволяет сформулировать еще один критерий планарности графов.

Граф G* называется абстрактно двойственным к графом G, если между множествами EG и EG* существуетбиcекция, обладающая тем свойством, что подмножество ребер из G обра­зует простой цикл в G тогда и только тогда, когда соответствующее ему подмножество ребер из G* об­разует разрез в G*.

На рис.40.4 изображены граф и абстрактно двойственный к нему граф. Соответствующие ребра обо­значены одной и той же буквой. Другой пример графов G и G* при­веден на рис. 40.5.

Понятие абстрактной двойственности обобщает понятиe геометрической двойственности, так как согласно теореме 40.3 справедливо

Утверждение 40.5. Граф, геометрически двойственный к плоскому графу, является абстрактно двойстнным к нему.

Непосредственно из определения вытекает следующее утверждение.

Утверждение 40.6. Граф Н является абстрактно двойственным к графу G тогда и только тогда, когда ма-

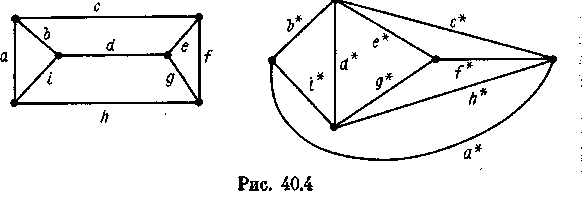
троид M(G) циклов графа G изоморфен матроиду М*(G) разрезов графа Н.

Теорема 40.7. Если граф G* — абстрактно двойственный к G, то G — граф, абстрактно двойственный к G*.

Отметим, что здесь, в отличие от теоремы 40.2, не требуется связность графа G.

На основании утверждения 40.6 матроид M(G) изо­морфен матроиду M*(G*). Поэтому в силу следствия 20.2 матроиды M*(G) и M**(G*) также изоморфны. Но M**(G*) = M(G*). Следовательно, матроид M(G*} цик­лов графа G* изоморфен матроиду M*(G) разрезов гра-

фа G, т. е. на основании утверждения 40.6 граф G явля­ется абстрактно двойственным к G*.

Таким образом, учитывая теорему 40.7, графы G и G* можно называть двойственными.

На вопрос о том, каждый ли подграф графа, имеюще­го двойственный граф, обладает двойственным графом, отвечает

Теорема 40.8. Пусть G и G* — двойственные графы, е = V₁V₂  EG, е* = v*₁v*₂ — соответствующее ребро гра­фа G*. Если Н—граф, полученный из графа G удале­нием ребра е, а Р — граф, полученный стягиванием реб­ра е* в G*, то Н и Р — двойственные графы, причем би­екция между множествами ЕН и ЕР остается такой же, как и между EG и EG*.

Любой простой цикл С графа Н = G — е является простым циклом и в графе G. Поэтому соответствующее множество ребер С* — разрез в G*, разделяющий мно­жество вершин VG* на два множества У₁ и V₂. По­скольку е*  С*, то вершины v₁* и v₂ *находятся одновре­менно либо вV₁* , либо в V*₂. Поэтому С* — разрез и в Р. Итак, каждому простому циклу графа Н соответству­ет разрез графа Р.

Пусть теперь С* — разрез в Р. Так как е* С*, то С* — разрез и в G*. Поэтому С — простой цикл графа G. Поскольку е  С, то С — простой цикл и в G. Следова­тельно, всякому разрезу в Р соответствует простой цикл в G.

Принимая во внимание, что всякий подграф H графа G можно получить из G удалением ребер, не принадле­жащих подграфу G, из теоремы 40.8 выводим

Следствие 40.9. Если граф имеет абстрактно двойственный граф, то всякий его подграф также имеет абстрактно двойственный граф.

Поскольку на основании теоремы 40.7 двум ребрам графа G, инцидентным вершине степени 2 (т. е. разрезу, опpеляющему эту вершину), соответствуют два кратных ребра (2-цикл) графа G*, то получаем еще одно следствиe теоремы 40.8.

Следствие 40.10. Если граф G имеет абстрактно двойственный граф, то любой граф, гомеоморфный графу также имеет абстрактно двойственный.

Теорема 40.11. Всякий планарный граф имеет абстрактно -двойственный к себе граф.

Для доказательства достаточно рассмотреть любую плоскую укладку G исходного планарного графа и граф геометрически двойственный к G. На основании

утверждения 40.5 граф G* — абстрактно-двойственный G. Оказывается, не всякий граф имеет абстрактно двойственный граф.

Утверждение 40.12. Граф Кз,з не имеет абстракт двойственного графа.

Доказательство проведем от противного. Допустим, граф Кз,з имеет двойственный граф G. Поскольку имеет лишь 4-циклы и 6-циклы, то граф G не имеет резов с менее чем четырьмя ребрами. Поэтому deg v  4 для всякой вершины v  VG. А из того, что граф Кз.з не имеет разрезов, состоящих из двух ребер, следует, что графе G нет 2-циклов, т. е. он не содержит кратных ребер. Следовательно, \G\  5. Суммируя все полученное и принимая во внимание лемму о рукопожатиях, выводим, \EG\  10. Но \EG\ = \ЕК₃,з\ = 9. Полученное противоречие доказывает утверждение 40.12. Утверждение 40.13. Граф К₅ не имеет абстрактно двойственного графа.

Допустим, что граф К₅ имеет двойственный графG. Так как граф К₅ не имеет циклов длины один или два, то степень каждой вершины графа G не менее 3. В то время из того, что граф К₅ имеет лишь разрезы, состоящие из 4 или 6 ребер, следует, что все простые циклы графа G имеют четную длину, т. е. G — двудольный граф. Если бы было \G\ 6, то получилось бы \EG\ 9, EG\ = \ЕК₅\ = 10. Итак, \G\  7. Поэтому граф G должен иметь по крайней мере 1/2 X 7 X 3 > 10 ребер.irq это противоречит условию \EG\ = 10.

Теперь мы можем доказать еще один критерий планарности графов.

Теорема 40.14 (X. Уитни, 1932 г.). Граф планарен тогда и только тогда когда он имеет абстрактно двой­ственный граф.

Необходимость установлена теоремой 40.11.

Достаточность докажем, показав, что непланарный граф G не имеет абстрактно двойственного. Согласно тео­реме Понтрягина — Куратовского граф G содержит под­граф Н, гомеоморфный Кз,з или К₅. Если бы граф G имел абстрактно двойственный граф, то по следствию 40.9 и подграф Н имел бы абстрактно двойственный граф. Но согласно следствию 40.10 это означало бы, что граф К₃,₃ или К₅ должен был иметь абстрактно двойствен­ный. Однако это противоречит утверждениям 40.12 и 40.13. Поэтому граф G не имеет абстрактно двойственно­го графа.

Из теорем 40.14 и 40.7 и утверждения 40.6 получаем

Следствие 40.15. Следующие утверждения эквива­лентны:

1. граф G планарен;

2. матроид циклов M(G) кографичен;

3. матроид разрезов М* (G) графичен.