§ 24. Объединение и пересечение матроидов

Пусть М1и М2 — два матроида на множестве элемен­тов Е с наборами независимых множеств I1 и I2 соот­ветственно. Положим

Как показывает прямая проверка, множество I удовлет­воряет аксиомам независимости. Следовательно, (Е, I) — матроид, для которого I служит набором независимых множеств. Этот матроид называется объединением мат­роидов М1 и М2 и обозначается через М1 M2.

Очевидно, что операция объединения матроидов ассо­циативна, и можно говорить об объединении нескольких матроидов.

Теорема 24.1. Пусть {Mi: i = 1,…,к} — семейство матроидов, определенных на одном и том же множестве Е, с ранговыми функциями ρi соответственно, k>1, M — объединение всех этих матроидов. Тогда ранговая функ­ция ρ матроида М определяется для любого подмножест­ва ХE равенством

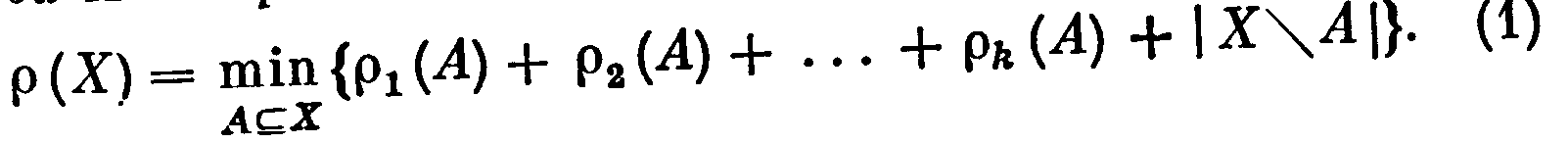> Рассмотрим отдельно два случая.

1. ρ (Х)=|Х|. В этом случав ρ (A)=|A| для любого подмножества AХ. Очевидно, что

поэтому

При А=Ø получаем

Равенство (1) доказано.

2. ρ(Х) < |Х|. Воспользуемся индукцией по k. Внача­ле пусть k = 2. По определению ρ(Х) = |В|, где В— мак­симальное независимое подмножество в X. Очевидно, что В = (В∩А) (В ∩ (Х\А)) для любого АХ. Так как

то для любого АХ

Теперь получим нижнюю оценку для ρ(Х). Пусть М2` — копия матроида М2, определенная на множестве Е`, имеющем пустое пересечение с Е. Более точно: Е = {e1,e2, ...,en}, Е`= {e`1,e`2, ..., е`n], Е∩Е`' = Ø, мно­жество {e`i1, e`i2,…,e`im } независимо относительно матрои­да М`2 тогда и только тогда, когда {ei1, ei2,…,eim } неза­висимо относительно М2. Очевидно, что можно определить матроид на множестве Е Е`, объявив его незави­симыми множествами объединения X Y, где ХЕ независимо относительно матроида M1, YE` — относительно М`2. Обозначим этот матроид и его ранговую функ­цию через М1М`2 и ρ` соответственно.

Пусть теперь X — произвольное подмножество мно­жества Е. Положив Si = {еi, е`i}, S= (Si: eiX), получим семейство S подмножеств множества Е Е`. Согласно следствию 22.2 для любого t≤|Х| частичная трансверсаль мощности t семейства S, независимая относительно матроида М1М`2, существует тогда и только тогда, когда для любых r подмножеств Si выполняется условие

Объединение множеств, заключенное в скобки, представим в виде A А`, где А Е, А' Е'. Ясно, что

поэтому условие (3) можно переписать так:

С другой стороны, легко понять, что следующие два утверждения равносильны:

1. существует частичная трансверсаль мощности t се­мейства подмножеств S, независимая относительно мат­роида М1М`2;

2. ρ(Х)≥t.

В самом деле, пусть Т — такая трансверсаль и пусть, . для определенности,

Тогда

и, следовательно,

т. е. выполняется условие (2).

Обратно, если выполняются условия (2) и (6), при­чем

то множество Т, определяемое условиями (5), является частичной трансверсалью мощности t семейства подмно­жеств S, независимой относительно матроида М1М`2.

Равносильность утверждений 1) и 2) доказана.

Из предыдущего вытекает, что ρ(Х)≥t тогда и только тогда, когда для любого подмножества А множества X верно неравенство (4). Следовательно, при t = ρ(Х)+ 1 в X существует такое подмножество Ао, которое не удовлет­воряет неравенству (4), т. е.

откуда

Из (7) и (2) вытекает

Последнее равенство в сочетании с неравенством (2) при­водит к формуле

Для k = 2 теорема доказана.

Пусть теперь k > 2 и теорема верна для объединения менее чем k матроидов. Если ρ` — ранговая функция объединения М1 М2... Мk-1, то в силу доказанного выше и индуктивного предположения имеем

Поскольку АВ и |B\A| + |X\B| = |Х\A|, то рассмат­риваемый минимум достигается лишь при А = В, и пото­му получаем

<

Ниже через (Е, ρ) обозначается матроид с множест­вом элементов Е и ранговой функцией ρ.

Следствие 24.2. Матроид (Е, ρ) имеет l попарно непересекающихся баз тогда и только тогда, когда для любого АЕ верно неравенство

> Пусть lМ — объединение l экземпляров матроида М, ρ` — ранговая функция этого объединения. Очевидно, что ρ`(lM) ≤ lρ(M) и М имеет l попарно непересекающихся баз только при условии ρ`(lM) = lρ(M). Теперь нужное утверждение непосредственно вытекает из предыдущей теоремы. <

Следствие 24.3. Для представимости множества Е в виде объединения не более чем l независимых подмно­жеств матроида М = (Е, ρ) необходимо и достаточно, что­бы любое подмножество АЕ удовлетворяло условию

> Множество Е представимо в виде указанного объединения только тогда, когда ρ`(lM) = |Е|. Согласно теореме 24.1 последнее равносильно неравенству |E| ≤ lρ(А)+ ||,в свою очередь равносильному неравенст­ву (9). <

Применим два предыдущих следствия к циклическому матроиду M(G) непустого графа G. В рассматриваемой ситуации независимыми множествами матроида служат множества ребер ациклических подграфов. Объединим каждый такой подграф со всеми не входящими в него вершинами G и будем считать подграф остовным. Для любого остовного подграфа Н верно равенство ρ(М(Н)) = n(G) - k(H). Если H — остовный подграф с множест­вом ребер А, то неравенства (8) и (9) превращаются в неравенства

и, соответственно,

Поэтому верны следующие два утверждения.

Следствие 24.4. В непустом графе G имеется l реберно непересекающихся остовов тогда и только тогда, когда любой его остовный подграф удовлетворяет нера­венству (10).

Следствие 24.5. Для того чтобы непустой граф G был объединением не более чем l своих остовов, не имею­щих общих ребер, необходимо и достаточно выполнение условия (11) для любого его остова Н.

Аналогично введенному выше понятию объединения матроидов можно ввести понятие их пересечения. Пусть Mj = (E, Ij) (j = 1,…,k) — k матроидов на множестве элементов Е с наборами независимых множеств Ij. Пару М = (Е, I),

назовем пересечением матроидов Mj (j = 1,…,k) и обозначим

Разумеется, пересечение матроидов также может ока­заться матроидом. Например, пересечение тривиального матроида и любого матроида с тем же множеством эле­ментов есть тривиальный матроид. Но, как правило, пере­сечение матроидов М не является матроидом с набором независимых множеств I, поскольку I может не удов­летворять аксиоме независимости I.2. Например, пересе­чение двух матроидов М1=(Е, I1) и М2=(Е, I2), где Е = {1, 2, 3, 4}, I1 = {Ø, {1}, {2}, {3}, {4}, {1, 3}, {1, 4}, {2, 3}, {2, 4}}, I2={ Ø, {1}, {2}, {3}, {4}, {1, 2}, {1, 4}, {2, 3}, {3, 4}}, не есть матроид, так как множество

I1 ∩ I2 ={0, {1}, {2}, {3}, {4}, {1, 4}, {2, 3}} не удовлетво­ряет условию I.2.

В § 28 читатель столкнется со следующей задачей:

Задача о пересечении k матроидов. Даны k матроидов на одном и том же множестве элементов Е. Требуется найти в Е наибольшее по числу элементов подмножество, являющееся независимым множеством каждого из заданных матроидов.

Пусть, например, заданы два графа G и Н, причем |EG| = |ЕН| = т. Пусть ребра этих графов занумерованы с помощью одних и тех же меток: EG = EH = {1, 2, ..., т}. Очевидно, что задача нахождения в Е наиболь­шего по числу элементов подмножества, не содержащего циклов ни первого, ни второго графов, и есть задача о пересечении двух графических матроидов M(G) и М(Н).

Задача о пересечении лишь двух матроидов стоит особняком: она эффективно решается методом чередую­щихся последовательностей (см., например, [25]). Идея этого метода демонстрируется в § 77.

При k > 2 задача о пересечении k матроидов стано­вится очень трудоемкой. Даже для решения ее простей­шего варианта — задачи о пересечении трех матроидов разбиений — не найдено, и скорей всего не существует, эффективных алгоритмов.

УПРАЖНЕНИЯ

1. Пусть М — матроид порядка п. Покажите, что число его баз не превосходит , а число его циклов не превосходит

2. Пусть М = (Е, I) — матроид с набором независимых множеств I, Ø ≠ A  Е. Пусть, далее, I` = {X  I: X ∩ А = Ø }. Докажите, что M` = (Е, I`) — матроид с набором независимых множеств I`. Матроид M` называется сужением матроида М посредством А.

3. Пусть в обозначениях предыдущего упражнения I`` = { X ∩ А : X  I}. Докажите, что M`` = (Е, I``) —матроид с набором независимых множеств I``. Матроид M`` называется ограничением матроида М на А.

4. Пусть Е — непустое конечное множество, k ≤ |Е|. Докажите, что множество β всех k-элемеятных подмножеств множества Е удовлетворяет аксиомам баз и, следовательно, (Е, β) — матроид. Его называют однородным матроидом ранга k.

5. Пусть D — ориентированный граф, и пусть Е и Y — два непересекающихся подмножества его вершин. Подмножество АЕ называется независимым, если существует |A| вершинно непересекающихся простых орцепей из A в Y. Докажите, что эти не­зависимые множества задают некоторый матроид.

6. Пусть М — матроид с ранговой функцией ρ. Докажите, что для любого подмножества А его элементов

ρ*(А) = |A| + ρ() - ρ (M),

где ρ* — коранговая функция матроида М.

7. Для каких k и п существуют однородные матроиды поряд­ка п и ранга k, являющиеся матроидами циклов некоторого графа?

8. Исследуйте циклические матроиды М(К5) и М(К3,3). Докажите, что они не являются кографическими.

9. Покажите, что с точностью до изоморфизма число матроидов порядка п не превосходит .

10. Охарактеризуйте графы, матроиды циклов и разрезов ко­торых изоморфны.

11. Покажите, что с точностью до изоморфизма существует ровно 4 матроида порядка 2 и 8 матроидов порядка 3. Сколько среди них представимых над каким-либо полем?

12. Пусть M1 и М2 — матроиды на множестве Е с ранговыми функциями ρ1 и ρ2. Докажите, что М1 и M2 имеют общее независимое множество мощности k тогда и только тогда, когда ρ1(A) + ρ2 () ≥ к для любого А  Е.

13. Докажите, что каждый однородный матроид является трансверсальным.

14. Докажите, что трансверсальные матроиды и только они представимы в виде объединений матроидов ранга 1.

15. Докажите, что циклический матроид М(К4) не является трансверсальным.

16. Докажите, что матроид, двойственный к трансверсальному, не обязательно является трансверсальным.

17. Докажите, что с точностью до изоморфизма число трансверсальных матроидов порядка п не превосходит .

18. Необходимо выполнить на ЭВМ множество заданий. Все задания требуют для выполнения одинакового времени. Каждому из заданий присвоен крайний срок выполнения.

а) Покажите, что набор всех подмножеств заданий, которые можно выполнить с соблюдением сроков выполнения, образует набор независимых подмножеств некоторого матроида.

б) Допустим, что за каждое не выполненное в срок задание необходимо заплатить штраф, величина которого одинакова для всех заданий. В каком порядке следует выполнять задания, чтобы общий штраф был минимальным?

19. Пусть М — матроид, элементам е которого приписаны не­ отрицательные веса w(e). Докажите, что

где β — множество баз матроида М, φ* — множество коциклов ма­троида М.