§ 59. Проблема четырех красок

Гипотеза четырех красок привлекала внимание мно­гих исследователей. Уже в 1880 году появилось первое доказательство А. Кемпе. Ошибка в этом доказательстве была обнаружена Р. Хивудом в 1890 году. Одновременно он показал, что если в формулировке гипотезы слово «четыре» заменить на «пять», то она легко доказывается.

Теорема 59.1 (Р. Хивуд, 1890 г.). Каждый планарный граф 5-раскрашиваем.

По-прежнему, не теряя общности, будем рассматри­вать плоские графы. Проведем доказательство индукцией по числу вершин графа. Теорема справедлива для графов с не более чем питью вершинами. Предположим, что она верна для графов порядка, не превосходящего n, п≥5.

Рассмотрим произвольный плоский граф G порядка n + 1. Согласно утверждению 38.5 этот граф содержит вершину v₀ , степень которой не превосходит пяти. Пусть N = N(v₀)—окружение вершины v₀ в графе G. Отдельно рассмотрим два случая.

1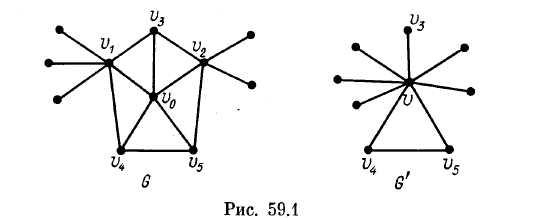) |N| ≤ 4. По индуктивному предположению граф G — v₀ 5-раскрашиваем; раскрасим его вершины пятью

цветами. Затем окрасим вершину v₀ в тот же из пяти цветов, который не использован при раскраске вер­шин из N.

2) |N| = 5. В множестве N существуют две несмеж­ные вершины v₁ и v₂, иначе G(N) = K5 и граф G не планарен. Граф G', полученный из G — v₀ слиянием этих вершин в вершину v (см. рис. 59.1), является плоским и по индуктивному предположению 5-раскрашиваемым. Фиксируем какую-либо из его правильных 5-раскрасок. В графе G окрасим вершины v₁ и v₂ в цвет вершины и, а остальные отличные от v вершины — в те же цвета, что и соответствующие вершины графа G'. Затем при­пишем вершине v₀ цвет, не использованный при раскра­ске вершин из N.

Таким образом, получена правильная 5-раскраска графа G.

Трудность проблемы четырех красок привела к появ­лению большого числа равносильных ей формулировок. Изучая эквивалентные задачи, исследователи пытались доказать гипотезу четырех красок.

Теорема 59.2. Следующие три утверждения экви­валентны:

1. произвольный плоский граф 4-раскрашиваем;

2. любая кубическая карта 4-раскрашиваема;

3) хроматический индекс произвольной кубической карты равен 3.

Вначале докажем истинность импликации 2) => 1). Согласно теореме 58.1 достаточно показать, что 4-раскраска произвольной карты определяется 4-раскраской некоторой кубической карты.

Пусть G — произвольная карта, и — ее вершина сте­пени 2. Замена ребер uv и uw, инцидентных вершине и, ребром vw приводит к новой карте G. Легко видеть, что правильная раскраска одной карты очевидным образом переносится на вторую. Поэтому без ограничения общности можно считать, что в графе G нет вершин второй зтепени.

Пустьи — произвольная вершина степени l≤4, V(u) = { v₁, v₂ ,… , v₁} — окружение вершины и, причем зершины в N(u) так занумерованы, что обход ребер в последовательности uv₁, uv₂ ,..., uv_i происходит в направлении движения часовой стрелки. Заменим вершину u простым циклом С =(u₁, u₂ ,… , u_i , u₁)и соединим u_i и v_i ребром, i = 1, l (рис. 59.2). Проводя аналогичную процедуру для каждой вершины графа G, степень которой больше трех, получим кубическую карту, которая,

Рис. 59.2

по предположению, 4-раскрашиваема. Искомая 4-раскраска граней карты G получается стягиванием каждого добавленного цикла в точку.

Теперь докажем, что 1) => 3). Пусть произвольный плоский граф 4-раскрашиваем. Рассмотрим некоторую кубическую карту G. Согласно теореме 58.1 эта карта тоже является 4-раскрапшваемой. Фиксируем одну из з 4-раскрасок и будем считать, что выбранные 4 цвета составляют абелеву группу А = {0 , а , b , а + b} = (а) + (b) — прямую сумму двух циклических групп второго порядка. (Это коммутативная группа, в которой а + а = b + b = 0.) Определив теперь цвет каждого ребра гра­фа G как сумму цветов двух разделяемых этим ребром граней, получим правильную раскраску ребер тремя цве­тами а, b, а + b.

Наконец, докажем, что 3) =>2). Пусть G — кубиче­ская карта и χ'(G) = 3. Фиксируем правильную ребер­ную 3-раскраску графа G цветами а, b и с. Рассмотрим подграф графа G, порожденный ребрами, окрашенными в цвета а и b. Очевидно, что этот подграф является объединением простых циклов. Припишем точкам пло­скости, лежащим внутри циклов, цвет 1, а вне — цвет 2. Аналогично, точкам плоскости, лежащим внутри циклов, индуцированных ребрами, имеющими цвета а и с, при­пишем цвет 3, а вне таких циклов — цвет 4. Таким об­разом, каждой грани карты G окажется приписанной одна из следующих пар цветов: (1, 3), (1, 4), (2, 3), (2, 4). Эти пары определяют раскраску карты четырьмя цветами, поскольку смежным граням соответствуют раз­ные пары.

В связи с проблемой четырех красок Г. Биркгоф в начале века поставил вопрос: какими свойствами должны обладать минимальные плоские графы, вершины кото­рых нельзя правильно раскрасить четырьмя цветами? Такие графы называются неприводимыми. Далее изуча­лись графы, их называли приводимыми конфигурация­ми, которые не являются подграфами неприводимых графов.

В дальнейшем многие математики изучали гипотети­ческие неприводимые графы и приводимые конфигура­ции. Эти исследования позволили довести число вершин в графах, для которых доказана их 4-раскрашиваемость, до 96.

В 1969 году X. Хееш свел проблему четырех красок к исследованию большого, но конечного множества U так называемых неустранимых конфигураций. Им было по­казано, что для любого максимального плоского графа G найдется подграф G’, изоморфный некоторой конфигура­ции из U и такой, что если граф G’ является 4-раскрашиваемым, то 4-раскрашиваем и граф G. Позже число таких неустранимых конфигураций было уменьшено до 1482. В 1976 году коллективу математиков и програм­мистов, возглавляемому К. Аппелем и В. Хейкеном, уда­лось правильно раскрасить все графы из множества U четырьмя цветами, затратив на это около 2000 часов ра­боты мощной ЭВМ, что позволило им заявить о доказа­тельстве гипотезы четырех красок. Тем не менее трудно согласиться с таким доказательством, поскольку и све­дение общего случая к неустранимым конфигурациям, и раскраску последних очень сложно повторить.

Понятия (плоской) карты и ее раскраски естественно распространяются на другие поверхности.

Пусть S — некоторая поверхность, любая карта на которой допускает раскраску χ(S) цветами, и существует карта на S, не допускающая раскраски χ(S)—1 цвета­ми. Тогда χ(S) называется хроматическим числом по­верхности S.

Теорема 59.3 (Г. Рингель, Д. Янгс, 1968 г.).Если S_p — сфера с р > 0 ручками, то

Подробно о раскраске карт, расположенных на про­извольных поверхностях, см. в [26].