ПРИМЕР ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА ДЛЯ ПЕРВОГО ВАРИАНТА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ФИЗИЧЕСКОГО ПРОЦЕССА

В соответствии с заданием модель представляет собой неизвестную функцию Y (функцию отклика) аргументами которой являются два фактора Х₁ и Х₂. Априорно известно, что функция Y гладкая, непрерывная и определена в области положительных значений. Реализация математической модели осуществлена в программе «Моделирование процессов вероятностного характера». С помощью этой программы можно производить численные эксперименты с заданной моделью в заданных пределах факторного пространства. По условиям первого варианта математической модели этой программы фактор Х₁ может изменяться в пределах от 2,3 до 3,8, а фактор Х₂ – в пределах от 2,4 до 4,2. Необходимо решить две задачи:

– найти значения факторов в заданных пределах, соответствующих наибольшему (экстремальному) значению функции отклика;

- найти интерполяционную функцию (уравнение регрессии), позволяющую вычислить значения функции отклика при любых значениях Х₁ и Х₂, лежащих в заданных диапазонах.

2. НАХОЖДЕНИЕ ЭКСТРЕМУМА МЕТОДОМ КРУТОГО ВОСХОЖДЕНИЯ

2.1 Выбор первоначальной подобласти исследования

Рассмотрим вопрос выбора подобласти исследования, используемой для определения градиента. На рис. 2.1 приведено графическое изображение области, в пределах которой рассматривается функция отклика в данном примере.

В связи с отсутствием каких либо предварительных данных о функции отклика, в качестве начальной точки при поиске экстремума выберем точку 0, лежащую в центре области факторного пространства (рис. 2.1) с координатами (Х₁=3,05, Х₂=3,3). Эта точка будет нулевым уровнем в первоначальной подобласти факторного пространства.

Следующим шагом является выбор размеров подобласти и определение кодированных значений уровней факторов по формуле

где - натуральное значение фактора; - натуральное значение основного уровня; - интервал варьирования; j – номер фактора.

В качестве размеров этой подобласти, примем 1/10 часть области факторного пространства по Х₁ и по Х₂. Это составит, соответственно, (3,8-2,3)/10=0,15 и (4,2-2,4)/10=0,18. При этом интервал по Х₁ равен 0,15/2=0,075, по Х₂ 0,18/2=0,09. Нижний уровень фактора в указанной подобласти Х₁ равен 3,05-0,075=2,975 (кодированное значение -1), а верхний 3,05+0,075=3,125(кодированное значение +1). Нижний уровень фактора Х₂ в этой подобласти равен 3,3-0,09=3,21 (кодированное значение -1), а верхний 3,3+0,09=3,39 (кодированное значение +1) . Отметим, что указанный выбор пока ничем не обоснован. Критерием правильности выбора является адекватность математической модели, используемой для аппроксимации функции Y. Указанные параметры подобласти факторного пространства (прямоугольник с точками 1,2,3,4) приведены на рис. 2.1.

В связи с тем, что количество факторов сравнительно мало, используем полный факторный эксперимент типа 2². В качестве математической модели функции отклика в выбранной подобласти факторного пространства принимаем полином первой степени адекватность которой достигается выбором соответствующих размеров исследуемой подобласти пространства.

Рис. 2.1. Иллюстрация области и подобласти факторного пространства. 0,1,2,3,4 – номера точек, используемых при планировании экспериментов

2.2. Составление плана экспериментов

В полном факторном эксперименте (ПФЭ) реализуются все возможные сочетания уровней факторов. Общее число опытов равно n=2^k, где k – число факторов. В рассматриваемом случае k=2, n=2²=4.

В табл. 2.1 приведены условия эксперимента в виде матрицы планирования, где строки соответствуют различным опытам, а столбцы – кодированным значениям факторов.

Таблица 2.1.

Таблица планирования для двух факторов 2².

№ опытов
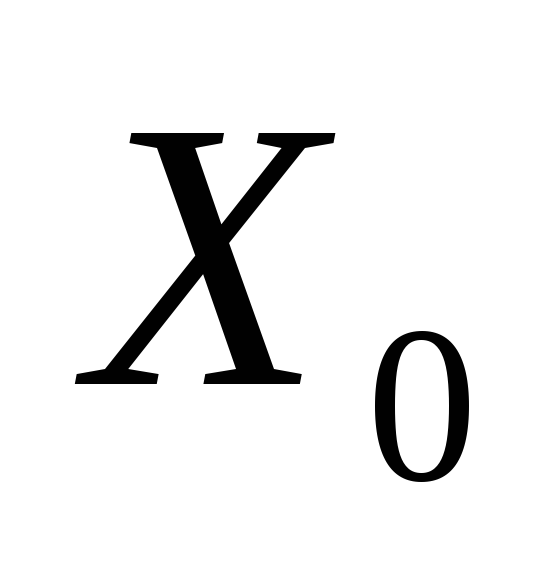
1	+	-	-
2	+	+	-
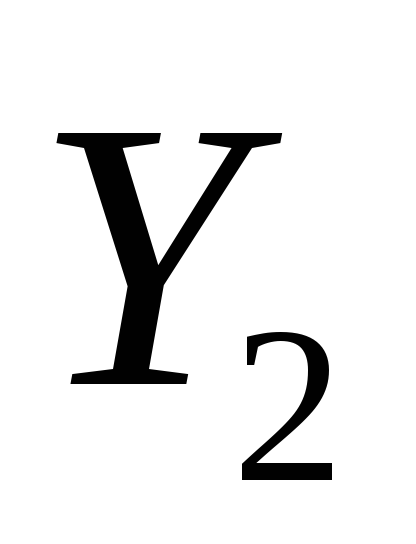
3	+	-	+
4	+	+	+

Примечание: номера опытов соответствуют номерам точек факторного пространства (рис. 2.1).

2.3. Проведение эксперимента и обработка результатов

При проведении экспериментов реализуются фактические значения факторов, соответствующие кодированным значениям. В табл. 2.2 приведены результаты численного эксперимента, выполненного в соответствии с принятым планом. Каждый опыт производился один раз (без проведения параллельных опытов). В графе приведены полученные значения функции отклика.

Для определения дисперсии Y и величины ошибки (среднеквадратического отклонения) проведем серию численных опытов при значениях факторов, соответствующих нулевому уровню (координатам центральной точки, указанной ранее).

Ориентируясь на условия проведения реальных экспериментов, связанных с значительными затратами времени и средств, ограничимся проведением трех численных опытов с помощью программы «Моделирование процессов вероятностного характера», результаты которых приведены ниже:

Y₁= 30,62 ; Y₂=30,82; Y₃=30,97; Y_ср= 30,8;

Таблица 2.2.

Результаты численного эксперимента

№ опытов
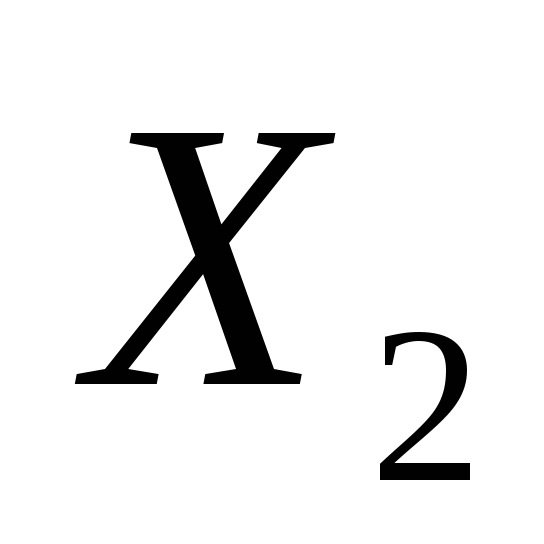
1	2,975	3,21	30,74
2	3,125	3,21	28,64
3	2,975	3,39	33,06
4	3,125	3,39	30,92

По результатам эксперимента находим значения коэффициентов по формуле:

В частности для модели и двух факторов

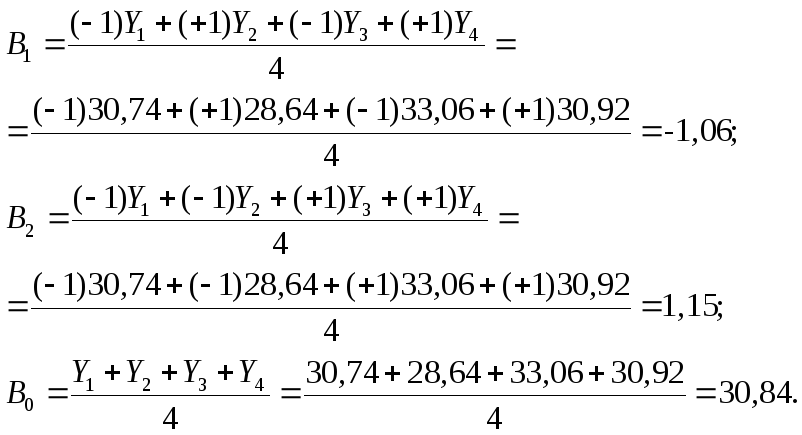
Значение коэффициента для каждого фактора соответствует вкладу данного фактора в параметр оптимизации при переходе фактора с нулевого уровня на верхний или нижний. Вклад, определенный при переходе от нижнего уровня к верхнему, называется эффектом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту.

В рассматриваемом случае

Проводим анализ адекватности выбранной модели (вида полинома) опытным данным по критерию Фишера F. Оценки дисперсий в формуле расчета критерия расставляются так, чтобы его величина была больше единицы

Оценку дисперсии адекватности в случае отсутствия дублирования опытов производим по формуле

где - расчетное значение Y, вычисленное по полученному уравнению регрессии при подстановке в него опытных данных значений Х_j; k – количество коэффициентов в уравнении регрессии; - число степеней свободы.

В рассматриваемом случае . Расчет приведен в табл. 2.3.

Таблица 2.3.

Расчет

№ опыта	Х1	Х2
1	-1	-1	30,75	30,74	0,0001
2	+1	-1	28,63	28,64	0,0001
3	-1	+1	33,05	33,06	0,0001
4	+1	+1	30,93	30,92	0,0001
Сумма	-	-	-	-	0,0004

Так как , то

Табличное значение F_Т при (для ), (для ) и уровне значимости 0,05 равно 200. То есть , что свидетельствует о том, что принятая модель адекватна. Об этом свидетельствует и сопоставление результатов расчета по полученному полиному и результатов эксперимента (табл. 2.1) – разница результатов имеет место в сотых.

Линейная модель не может быть адекватной, если оказался значимым хотя бы один эффект взаимодействия.

Проверяем статистическую значимость коэффициентов полинома. Доверительный интервал для j- того коэффициента определяется по формуле

Здесь t=4,3 – квантиль распределения Стьюдента при числе степеней свободы , с которыми определялась дисперсия для вероятности 0,95, равной выбранному уровню значимости 0,05. Доверительные интервалы

Как следует из полученных выражений, все коэффициенты не равны нулю и являются следовательно статистически значимыми.

При оценке адекватности модели возможны следующие случаи: