
- •Г. В. Красоленко, н. В. Сванидзе, г. В. Якунина Обыкновенные дифференциальные уравнения. Ряды
- •Введение
- •Фамилия, имя, отчество
- •Примерный вариант контрольной работы № 5
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Решение задачи № 5
- •Примерный вариант контрольной работы № 6 по теме « Ряды»
- •Решение задачи № 1
- •Решение задачи № 2
- •Решение задачи № 3
- •Решение задачи № 4
- •Решение задачи № 5
- •Контрольная работа № 5 по теме « Обыкновенные дифференциальные уравнения»
- •Контрольная работа № 6 по теме « Ряды»
- •Рекомендуемая литература
- •Оглавление
- •Обыкновенные дифференциальные уравнения. Ряды
- •190005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.
Решение задачи № 4
Найдем общее решение уравнения
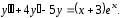 (14)
(14)
Это
линейное неоднородное уравнение второго
порядка с постоянными коэффициентами.
Его общее решение ищем в виде
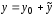 .
Неоднородному уравнению (14) соответствует
однородное уравнение
.
Неоднородному уравнению (14) соответствует
однородное уравнение
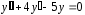 .
(15)
.
(15)
Функция
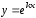 является решением уравнения (15), если
является решением уравнения (15), если есть корень характеристического
уравнения
есть корень характеристического
уравнения
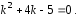 (16)
(16)
Оно
имеет корни
 (вещественные и различные). Следовательно,
общее решение однородного уравнения
(15) имеет вид
(вещественные и различные). Следовательно,
общее решение однородного уравнения
(15) имеет вид
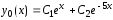 .
.
Построим
теперь частное решение
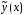 уравнения (14). В нашем случае правая
часть уравнения (14)
уравнения (14). В нашем случае правая
часть уравнения (14)
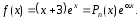
Сравнивая
два последних выражения, получаем
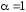 и
и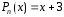 – многочлен
первой степени,
– многочлен
первой степени,
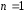 .
.
Поскольку
контрольное число
 совпадает с корнем характеристического
уравнения
совпадает с корнем характеристического
уравнения (
(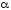 –
простой корень характеристического
уравнения (16)), частное решение уравнения
(14) следует искать в виде
–
простой корень характеристического
уравнения (16)), частное решение уравнения
(14) следует искать в виде
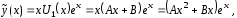
где
коэффициенты
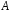 и
и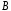 подлежат определению.
подлежат определению.
Чтобы
найти
 и
и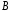 ,
подставим
,
подставим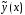 и его производные в исходное уравнение
(14). Здесь при вычислении
и его производные в исходное уравнение
(14). Здесь при вычислении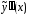 удобно воспользоваться формулой
удобно воспользоваться формулой .
.
Итак,
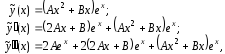
и левая часть уравнения (14) принимает вид

В
результате для определения коэффициентов
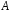 и
и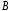 получаем уравнение
получаем уравнение

обе
части которого можно сократить на
множитель
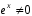 .
.
Коэффициенты
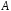 и
и должны быть такими, чтобы обе части
уравнения (14) были тождественно равны
друг другу, т.е.
должны быть такими, чтобы обе части
уравнения (14) были тождественно равны
друг другу, т.е.
 .
(17)
.
(17)
Тождество
(17) выполняется тогда и только тогда,
когда слева и справа стоят одинаковые
коэффициенты при одинаковых степенях
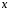 :
:

Следовательно,
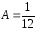 ,
, ,
а
,
а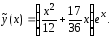
Таким образом, общее решение уравнения (14) имеет вид

Ответ.
Общим решением уравнения (14) является функция

определенная
на интервале
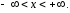
Рассмотрим решение линейного неоднородного уравнения (1) со специальной правой частью
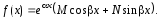
Предполагается,
что контрольные числа
 мнимые, т. е.
мнимые, т. е. ,
а
,
а и
и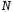 – вещественные числа, заданные многочлены
нулевой степени (см. формулу (2)).
– вещественные числа, заданные многочлены
нулевой степени (см. формулу (2)).
Уравнение (1) в этом случае принимает вид
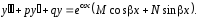 (18)
(18)
Уравнению (18) соответствует однородное уравнение
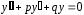
с характеристическим уравнением
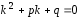 .
(19)
.
(19)
Пусть
 и
и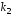 его корни.
его корни.
Имеет место следующее утверждение (см. [2]).
Утверждение 4.
Частное решение уравнения (18) следует искать в виде:
если контрольные числа
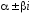 не являются корнями характеристического
уравнения (19), т.е.
не являются корнями характеристического
уравнения (19), т.е.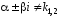 ,
то
,
то
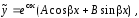
где
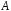 и
и – неизвестные числа, подлежащие
дальнейшему определению;
– неизвестные числа, подлежащие
дальнейшему определению;
если контрольные числа
 являются корнями характеристического
уравнения (19), т.е.
являются корнями характеристического
уравнения (19), т.е. ,
то
,
то

Заметим,
что искомое частное решение всегда
содержит оба слагаемых
 вне зависимости от того, содержит ли
функция, стоящая в правой части уравнения
(18), одновременно
вне зависимости от того, содержит ли
функция, стоящая в правой части уравнения
(18), одновременно и
и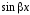 .
.
Числа
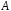 и
и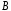 определяются непосредственной
подстановкой решения
определяются непосредственной
подстановкой решения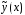 и его производных в уравнение (18).
и его производных в уравнение (18).
Для
того чтобы уравнение превратилось в
тождество, приравняем коэффициенты при
 и
и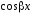 в его левой и правой частях.
в его левой и правой частях.
В
результате получим систему линейных
уравнений для нахождения
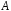 и
и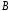 .
.
Решение задачи № 5
Решить задачу Коши:
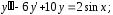 (20)
(20)
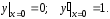 (21)
(21)
Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами.
Его
общее решение ищем в виде
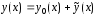 .
.
Неоднородному уравнению (20) соответствует однородное уравнение
 (22)
(22)
Функция
 является решением уравнения (22) в том
случае, если
является решением уравнения (22) в том
случае, если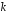 есть
корень характеристического уравнения
есть
корень характеристического уравнения
 (23)
(23)
Оно имеет два комплексно сопряженных корня
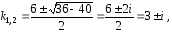
т.е.
 ,
где
,
где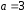 и
и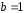 .
.
Следовательно, общее решение однородного уравнения (22) в соответствии с формулой (11) имеет вид
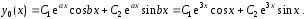
Построим
теперь частное решение
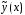 уравнения (20).
уравнения (20).
Для уравнения (20)

Отсюда
имеем
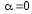 ,
,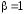 ,
,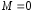 и
и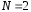 .
.
Частное
решение
 следует искать в виде
следует искать в виде
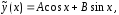
поскольку
контрольные числа
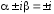 не совпадают с корнями
не совпадают с корнями характеристического уравнения (23).
характеристического уравнения (23).
Коэффициенты
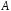 и
и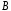 подлежат определению.
подлежат определению.
Вычислим
первую и вторую производные функции
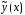

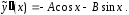
После
подстановки
 ,
, и
и в левую часть (20) имеем:
в левую часть (20) имеем:
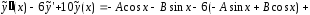

Следовательно,
 и
и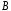 должны обеспечивать выполнение тождества
должны обеспечивать выполнение тождества

Отсюда,
приравнивая коэффициенты при
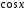 и
и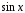 в его левой и правой частях, получим
систему линейных уравнений с двумя
неизвестными
в его левой и правой частях, получим
систему линейных уравнений с двумя
неизвестными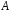 и
и :
:

Решая эту систему, находим

Общее решение уравнения (20) имеет вид
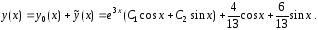 (24)
(24)
Найдем
теперь значения постоянных
 и
и ,
при которых выполняются начальные
условия (21). Согласно первому из них
,
при которых выполняются начальные
условия (21). Согласно первому из них

откуда
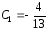 .
.
Продифференцируем общее решение (24)

Согласно второму из равенств (21) имеем
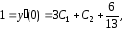
откуда
найдем
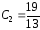 .
.
Подставив
найденные значения
 и
и в общее решение (24), получаем искомое
частное решение
в общее решение (24), получаем искомое
частное решение
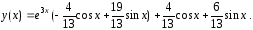
Ответ.
Решением
задачи Коши (20),(21) является функция
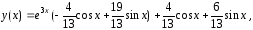
определенная
на интервале

