
- •Решение:
- •1). Располагаем значение результатов эксперимента в порядке возрастания, т.Е. Записываем вариационный ряд:
- •2). Находим размах варьирования: .
- •Задание II
- •Решение:
- •Задание I
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Критические точки распределения Пирсона
Элементы математической статистики
Решение типового варианта
Задание I
В результате эксперимента получены данные, записанные в виде статистического ряда:
Требуется:
-
записать значения результатов эксперимента в виде вариационного ряда;
-
найти размах варьирования и разбить его на ряд частичных интервалов;
-
построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
-
найти числовые характеристики выборки (математическое ожидание, дисперсию, среднее квадратическое отклонение);
-
приняв в качестве нулевой гипотезу
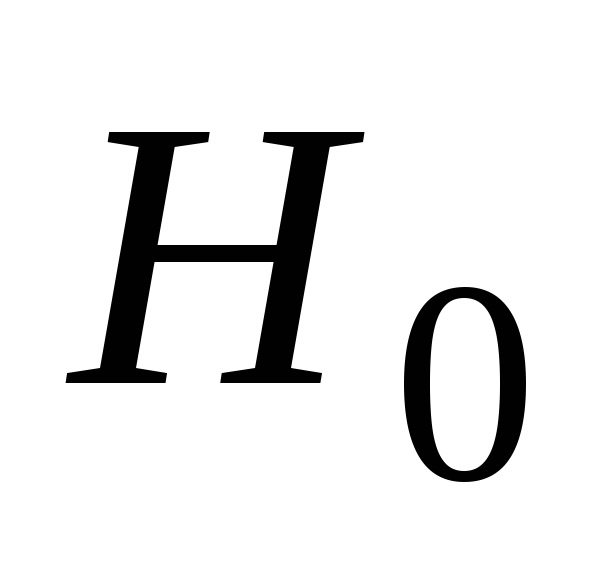 :
генеральная совокупность, из которой
извлечена выборка, имеет нормальное
распределение, проверить её, критерием
Пирсона при уровне значимости
:
генеральная совокупность, из которой
извлечена выборка, имеет нормальное
распределение, проверить её, критерием
Пирсона при уровне значимости
 ;
; -
найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности
 .
.
-
44,8
46,2
45,6
44,0
46,4
45,2
46,7.
45,4
45,3
46,1
44,3
45,3
45,6
46,7
44,5
46,0
45,7
45,0
46,4
45,9
44,4
45,4
46,1
43,4
46,5
45,9
43,9
45,7
47,1
44,9
43,8
45,6
45,2
46,4
44,2
46,5
45,7
44,7
46,0
45,8
44,3
45,5
46,7
44,9
46,2
46,7
44,6
46,0
45,4
45,0
45,4
45,3
44,1
46,6
44,8
45,6
43,7
46,8
45,2
46,1
44,5
45,4
45,1
46,2
44,2
46,4
45,7
43,9
47,2
45,0
43,9
45,6
44,9
44,5
46,2
46.7
44,3
46,1
47,7
45,8
45,6
45,2
44,2
46,0
44,7
46,5
43,5
45,4
47,1
44,0
46,2
44,2
45,5
46,0
45,7
46,4
44,6
47,0
45,2
46,9
Решение:
1). Располагаем значение результатов эксперимента в порядке возрастания, т.Е. Записываем вариационный ряд:
-
43,4
43,5
43,7
43,8
43,9
43,9
43,9
44,0
44,0
44,1
44,2
44,2
44,2
44,3
44,3
44,3
44,4
44,5
44,5
44,5
44,6
44,6
44,7
44,7
44,8
44,8
44,8
44,9
44,9
44,9
45,0
45,0
45,1
45,2
45,2
45,2
45,2
45,2
45,3
45,3
45,3
45,4
45,4
45,4
45,4
45,4
45,4
45,5
45,5
45,6
45,6
45,6
45,6
45,6
45,7
45,7
45,7
45,7
45,7
45,7
45,8
45,8
45,9
45,9
46,0
46,0
46,0
46,0
46,0
46,0
46,1
46,1
46,1
46,1
46,2
46,2
46,2
46,2
46,2
46,4
46,4
46,4
46,4
46,4
46,5
46,5
46,5
46,6
46,7
46,7
46,7
46,7
46,7
46,8
46,9
47,0
47,1
47,1
47,2
47,7
2). Находим размах варьирования: .
Иногда для определения данных интервала
используют формулу
![]() ,
где
,
где
![]() - объем выборки. За величину частичного
интервала
- объем выборки. За величину частичного
интервала
![]() принимается некоторое удобное число,
ближайшее к полученному
принимается некоторое удобное число,
ближайшее к полученному
![]() .
Число таких интервалов определяется
формулой
.
Число таких интервалов определяется
формулой
![]() .
В качестве границы первого интервала
можно выбрать значение
.
В качестве границы первого интервала
можно выбрать значение
![]() .
Тогда границы следующих частичных
интервалов вычисляем по формуле
.
Тогда границы следующих частичных
интервалов вычисляем по формуле
![]() ,
где
,
где
![]() принимает значения от 1 до
принимает значения от 1 до
![]() .
.
В нашем примере
![]() .
Объём выборки
.
Объём выборки
![]() ,
тогда
,
тогда
![]() .
Примем за
.
Примем за
![]() .
Следовательно, разобьем наш вариационный
ряд на
.
Следовательно, разобьем наш вариационный
ряд на
![]() интервалов.
интервалов.
Находим середины интервалов:
![]() .
Подсчитываем число значений результатов
эксперимента, попавших в каждый
интервал, т.е. находим частоты интервалов
.
Подсчитываем число значений результатов
эксперимента, попавших в каждый
интервал, т.е. находим частоты интервалов
![]() .
Далее вычисляем относительные
частоты
.
Далее вычисляем относительные
частоты
![]() и их плотности
и их плотности
![]() .
Все полученные
результаты помещаем в таблицу
(табл. 1).
.
Все полученные
результаты помещаем в таблицу
(табл. 1).
![]()
Таблица 1.
-
Номер
частичного интервала i
Границы
интервала
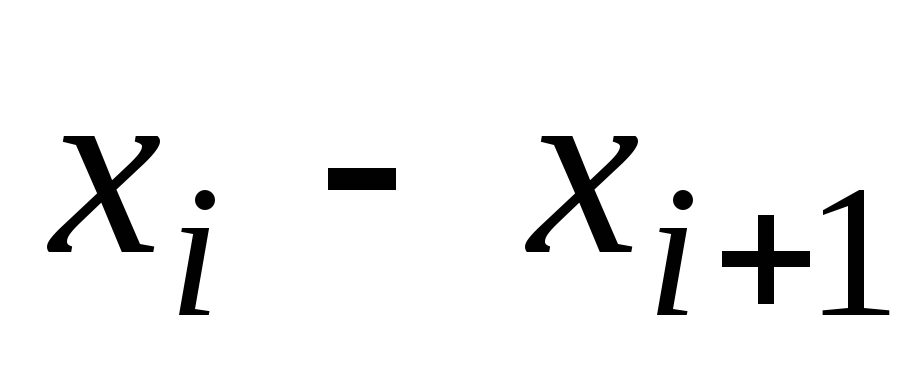
Середина интервала
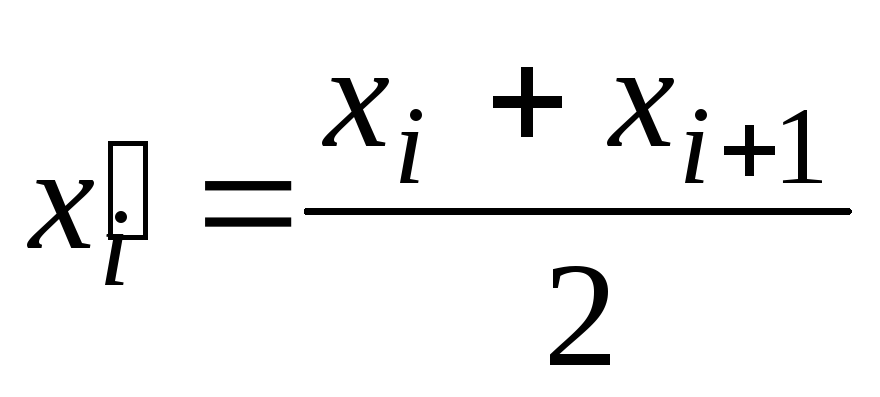
Частота
интервала
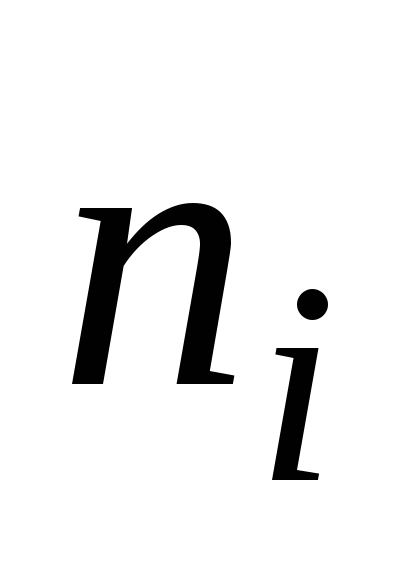
Относительная частота
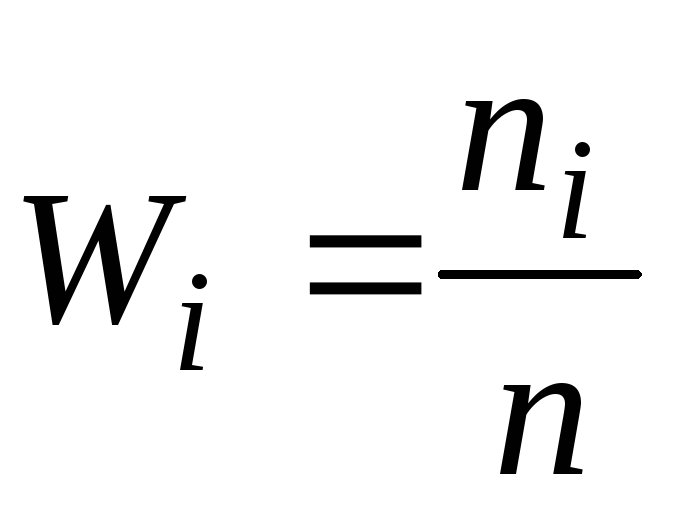
Плотность относитель-
ной частоты
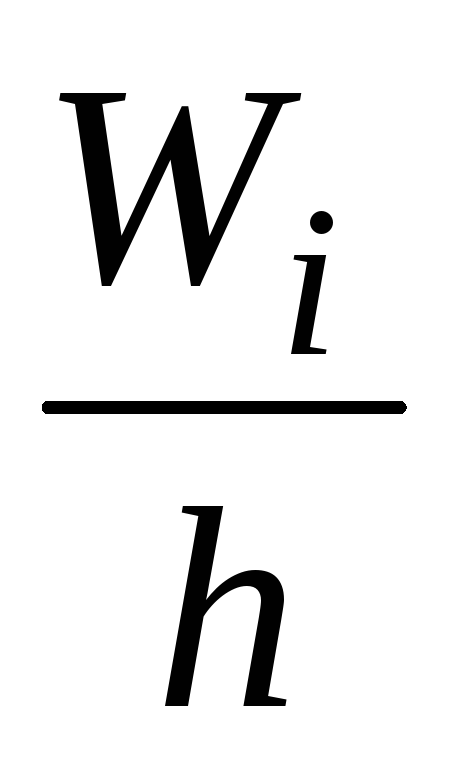
1
43,40 – 43,96
43,68
7
0,07
0,13
2
43,96 – 44,52
44,24
13
0,13
0,23
3
44,52 – 45,08
44,80
12
0,12
0,21
4
45,08 – 45,64
45,36
22
0,22
0,39
5
45,64 – 46,20
45,92
25
0,25
0,45
6
46,20 – 46,76
46,48
14
0,14
0,25
7
46,76 – 47,32
47,04
6
0,06
0,11
8
47,32 – 47,88
47,60
1
0,01
0,02
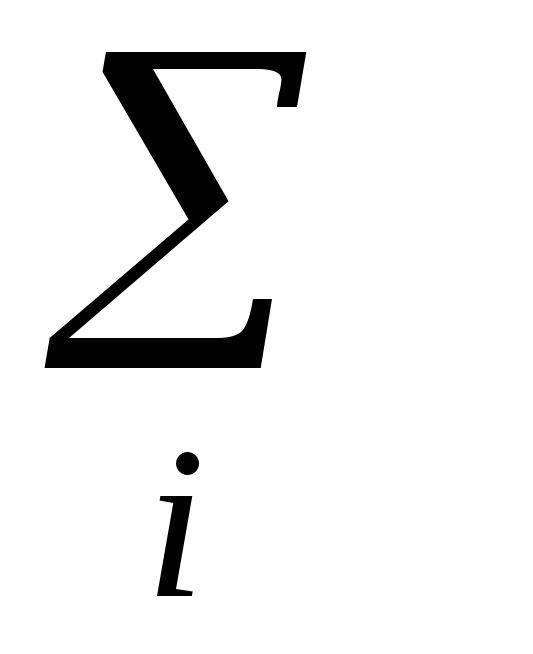
–
100
–
3). Строим полигон частот – ломанную
линию, отрезки которой соединяют точки
![]() ,
,
![]() ,
…,
,
…,
![]() (рис. 1) и гистограмму относительных
частот – ступенчатую фигуру, состоящую
из прямоугольников, основаниями которой
служат частичные интервалы, длиною
(рис. 1) и гистограмму относительных
частот – ступенчатую фигуру, состоящую
из прямоугольников, основаниями которой
служат частичные интервалы, длиною
![]() ,
а высоты равны плотности
относительной частоты
,
а высоты равны плотности
относительной частоты
![]() (рис.2).
(рис.2).
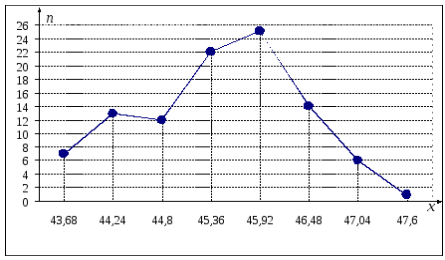
Рис. 1. Полигон частот
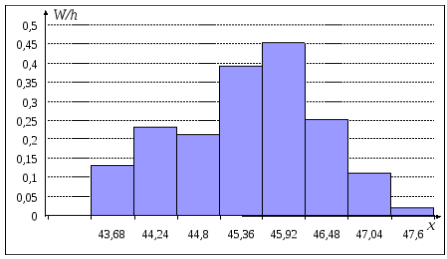
Рис.2. Гистограмма относительных частот
Найдем значения эмпирической функции
распределения (функции распределения
выборки) – функции, определяющей для
каждого значения
![]() относительную частоту события
относительную частоту события
![]() .
.
Итак, по определению,
![]() ,
,
где
![]() - число вариант, меньших
- число вариант, меньших
![]() ;
;
![]() - объём выборки.
- объём выборки.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Строим график эмпирической функции
распределения (рис. 3).
![]()
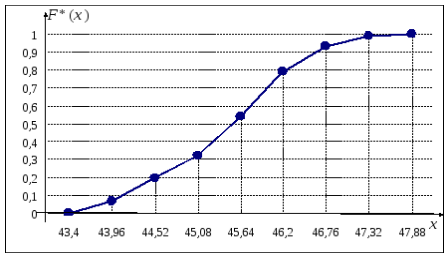
Рис. 3. График эмпирической функции распределения
4). Находим выборочное среднее:
![]()
и выборочную
дисперсию:
![]() .
.
Для этого составляем расчетную таблицу (табл. 2).
Таблица 2.
|
|
Границы интервала
|
Середина интервала
|
Частота
интервала
|
|
|
|
|
1 |
43,40 – 43,96 |
43,68 |
7 |
305,76 |
1907,94 |
13355,60 |
|
2 |
43,96 – 44,52 |
44,24 |
13 |
575,12 |
1957,18 |
25443,31 |
|
3 |
44,52 – 45,08 |
44,80 |
12 |
537,60 |
2007,04 |
24084,48 |
|
4 |
45,08 – 45,64 |
45,36 |
22 |
997,92 |
2057,53 |
45265,65 |
|
5 |
45,64 – 46,20 |
45,92 |
25 |
1148,00 |
2108,65 |
52716,16 |
|
6 |
46,20 – 46,76 |
46,48 |
14 |
650,72 |
2160,39 |
30245,47 |
|
7 |
46,76 – 47,32 |
47,04 |
6 |
282,24 |
2212,76 |
13276,57 |
|
8 |
47,32 – 47,88 |
47,60 |
1 |
47,60 |
2265,76 |
2265,76 |
|
|
|
– |
100 |
4544,96 |
– |
206653 |
Из нее получаем:
![]() ,
,
![]() ,
,
![]() .
.
Несмещённой
называют
статистическую оценку
![]() ,
математическое ожидание которой равно
оцениваемому параметру
,
математическое ожидание которой равно
оцениваемому параметру
![]() при любом объёме выборки.
при любом объёме выборки.
Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Выборочная дисперсия является смещенной оценкой генеральной дисперсии, а исправленная дисперсия - несмещенной оценкой:
![]() ,
,
![]() .
.
5).
Критерием
согласия
называют критерий проверки гипотезы
о предполагаемом законе неизвестного
распределения. Имеется несколько
критериев согласия:
![]() («хи квадрат») К. Пирсона, Колмагорова,
Фишера, Смирнова и др.
(«хи квадрат») К. Пирсона, Колмагорова,
Фишера, Смирнова и др.
По условию задачи нам необходимо использовать критерий Пирсона, правило применения которого сводится к следующему:
-
вычислить теоретические частоты, затем наблюдаемое значение критерия по формуле
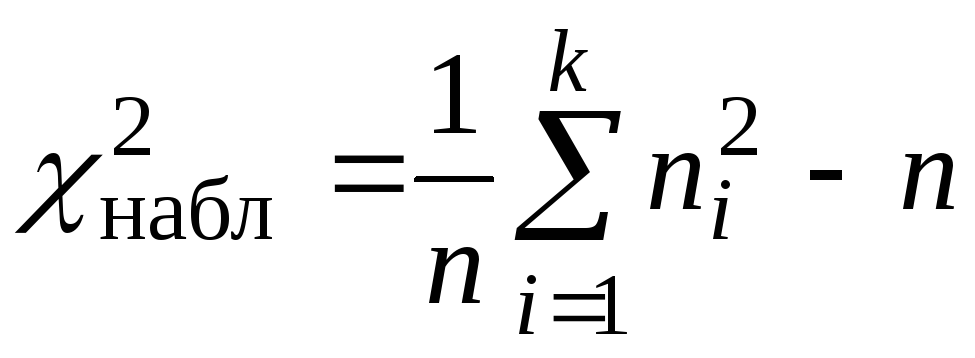 ;
; -
по таблице критических точек распределения
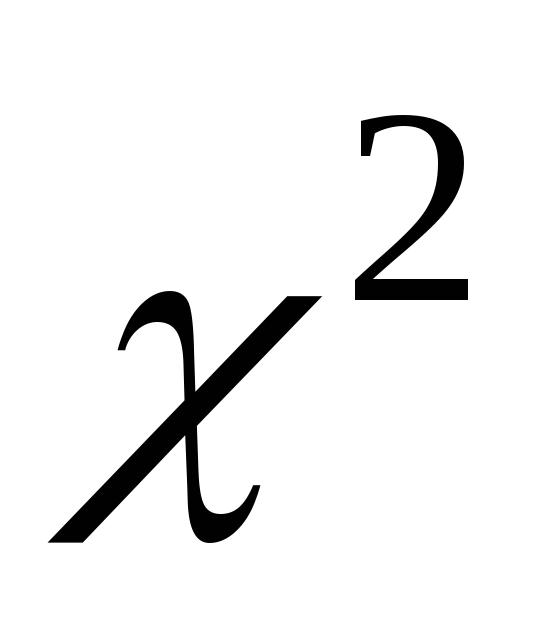 ,
по заданному уровню значимости
,
по заданному уровню значимости
 и числу степеней свободы
и числу степеней свободы
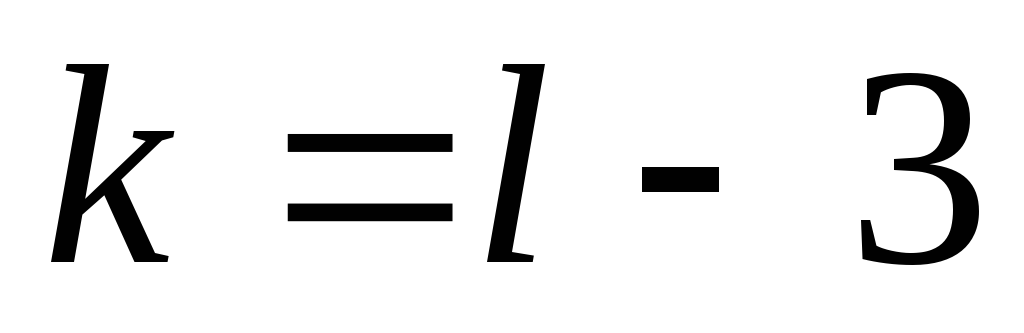 ,
где
,
где
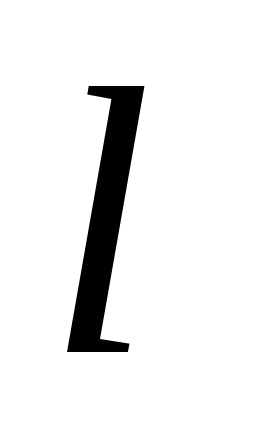 – число интервалов, найти критическую
точку
– число интервалов, найти критическую
точку
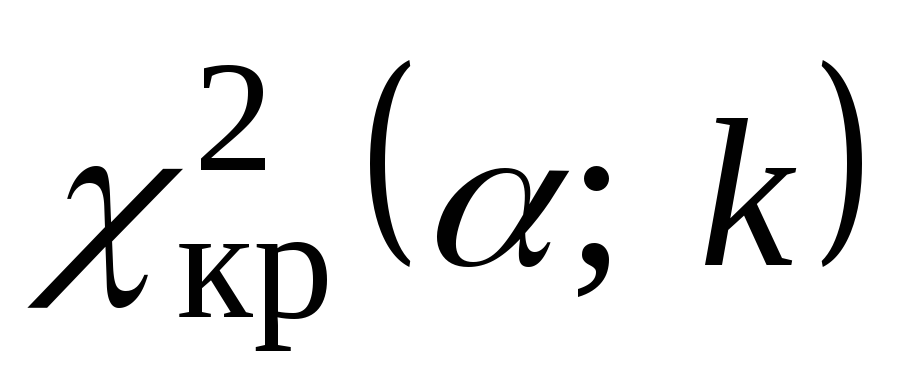 ;
; -
если
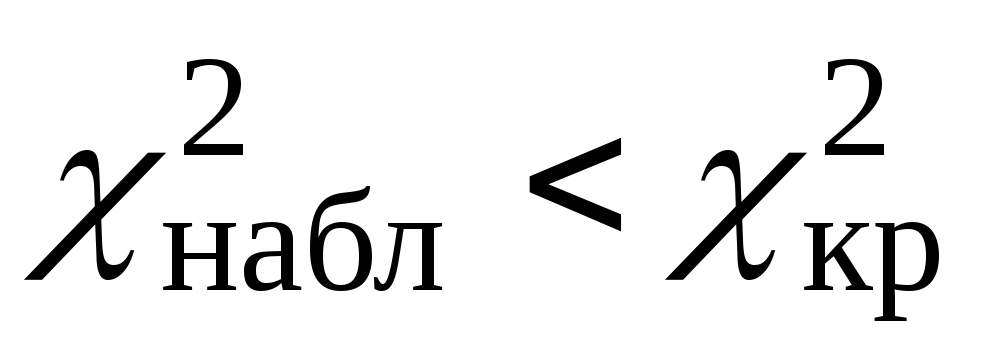 – нет оснований
отвергать нулевую гипотезу;
– нет оснований
отвергать нулевую гипотезу;
если
![]() – нулевую
гипотезу отвергают.
– нулевую
гипотезу отвергают.
Согласно критерию
Пирсона необходимо сравнить эмпирические
и теоретические частоты. Эмпирические
частоты даны.
Найдем теоретические частоты. Для этого
пронумеруем
![]() ,
т.е. перейдем
к случайной величине
,
т.е. перейдем
к случайной величине
![]() и вычислим концы интервалов:
и вычислим концы интервалов:
![]() и
и
![]() .
Наименьшее
значение
.
Наименьшее
значение
![]() положим
стремящимся к
положим
стремящимся к
![]() ,
а наибольшее
–
,
а наибольшее
–
![]() ,
стремящимся к
,
стремящимся к
![]() .
Результаты занесем в таблицу (табл.
3). Число наблюдений
.
Результаты занесем в таблицу (табл.
3). Число наблюдений
![]() в отдельных интервалах должно быть
достаточно большим (рекомендуется
иметь в каждом интервале не менее 5-10
наблюдений). Если
в отдельных интервалах должно быть
достаточно большим (рекомендуется
иметь в каждом интервале не менее 5-10
наблюдений). Если
![]() в отдельных интервалах очень малы,
следует объединить интервалы. Длины
интервалов могут быть различными. В
соответствии с этим число исходных
интервалов может быть уменьшено. Так
как
в отдельных интервалах очень малы,
следует объединить интервалы. Длины
интервалов могут быть различными. В
соответствии с этим число исходных
интервалов может быть уменьшено. Так
как
![]() ,
то последний девятый интервал объединим
с восьмым и получим интервал
,
то последний девятый интервал объединим
с восьмым и получим интервал
![]() с частотой
с частотой
![]() .
.
Таблица 3.
-
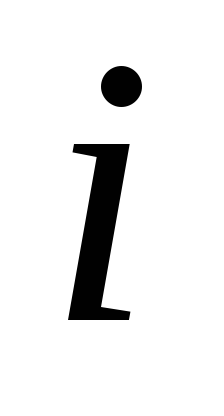
Границы интервала

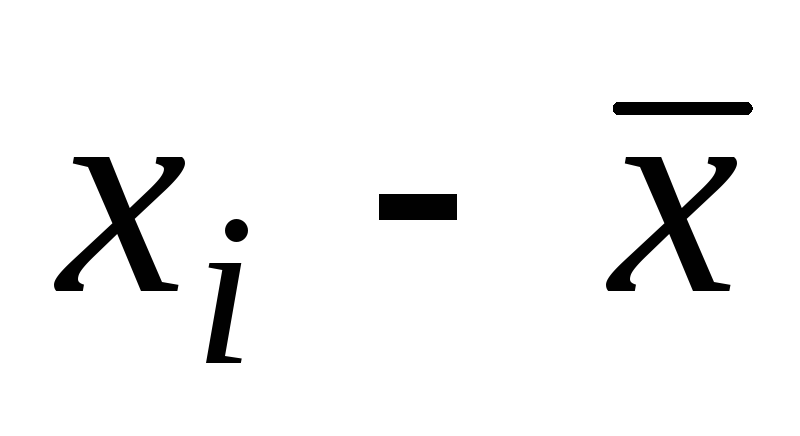

Границы интервала
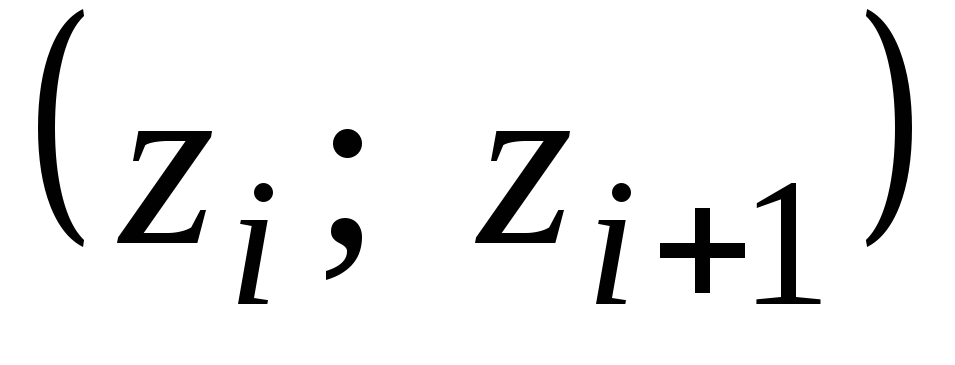

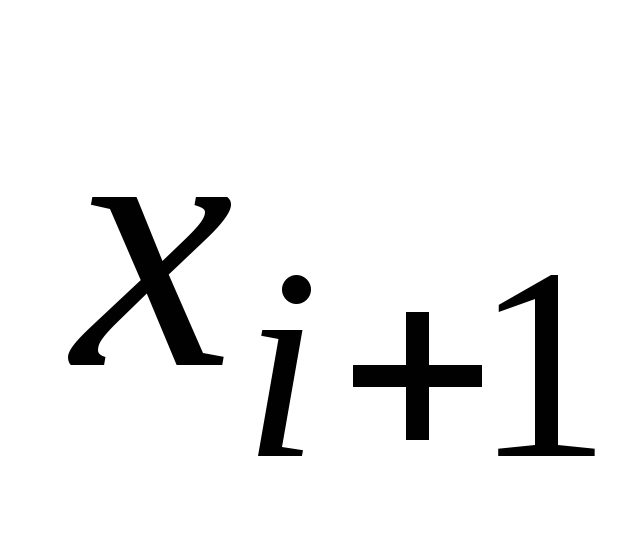
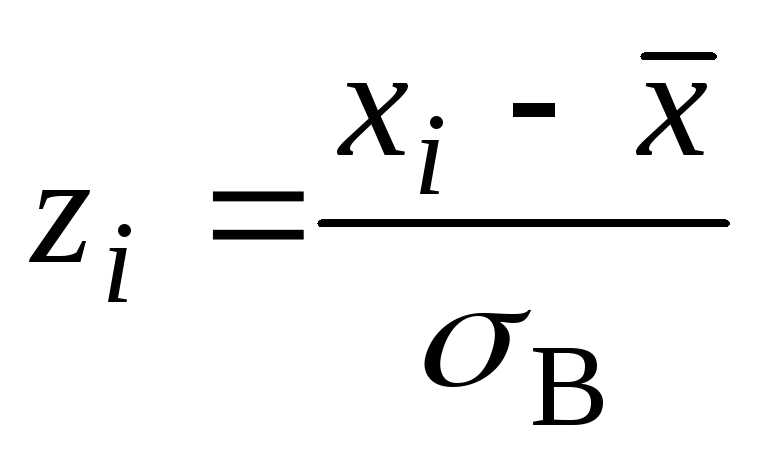
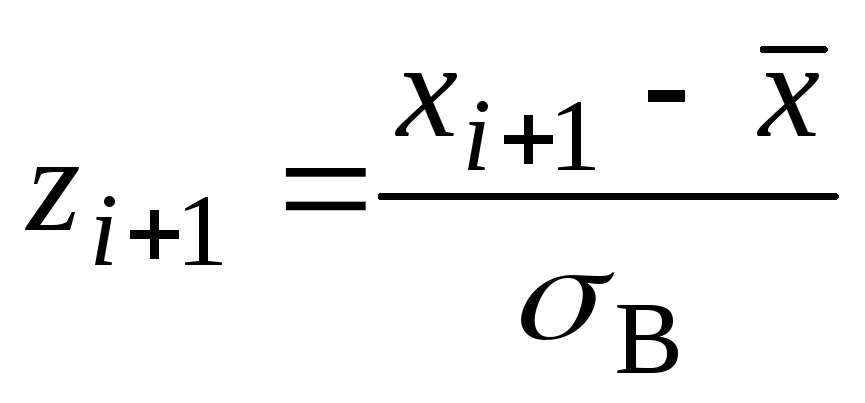
1
43,40 44,96
–
-0,49
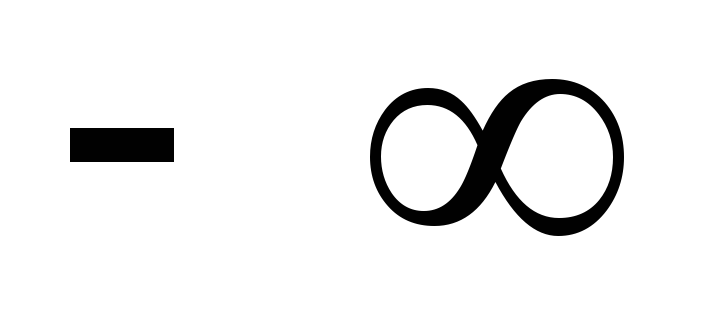
-1,31
2
43,96 44,52
-0,49
-0,93
-1,31
-1,02
3
44,52 45,08
-0,93
-0,37
-1,02
-0,41
4
45,08 45,64
-0,37
0,19
-0,41
0,21
5
45,64 46,20
0,19
0,75
0,21
0,82
6
46,20 46,76
0,75
1,31
0,82
1,44
7
46,76 47,88
1,31
–
1,44

Находим теоретические
вероятности
![]() и теоретические
частоты:
и теоретические
частоты:
![]() .
Составляем расчетную таблицу (табл.
4). Значения функции
.
Составляем расчетную таблицу (табл.
4). Значения функции
![]() берём из прил.1.
берём из прил.1.
Таблица 4.
-
Границы интервала

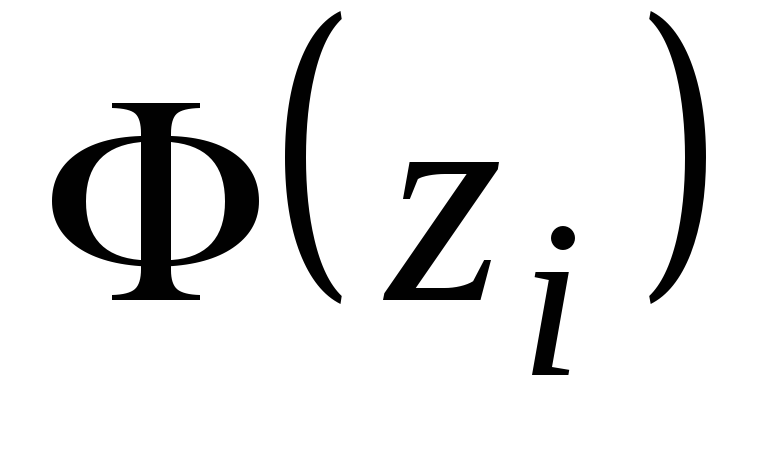
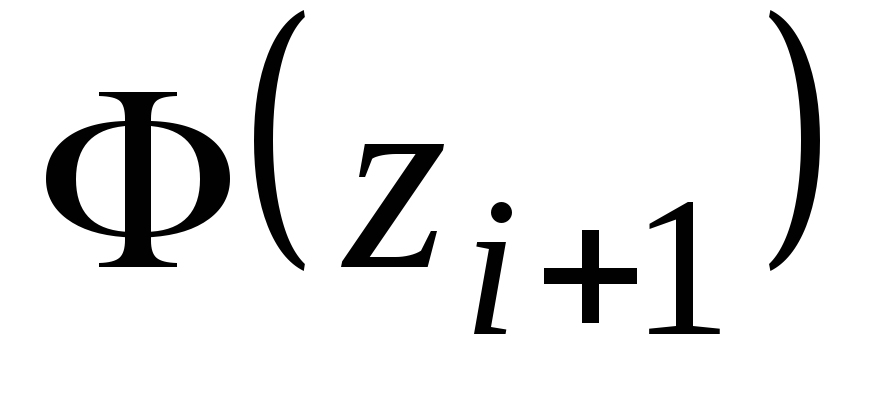
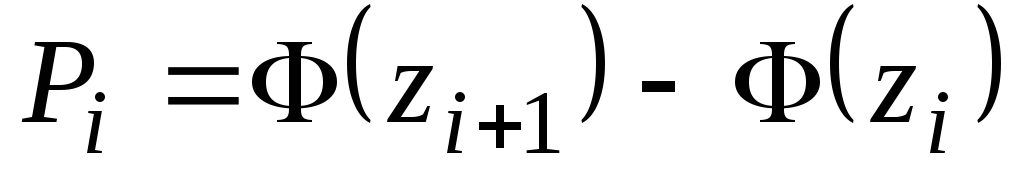
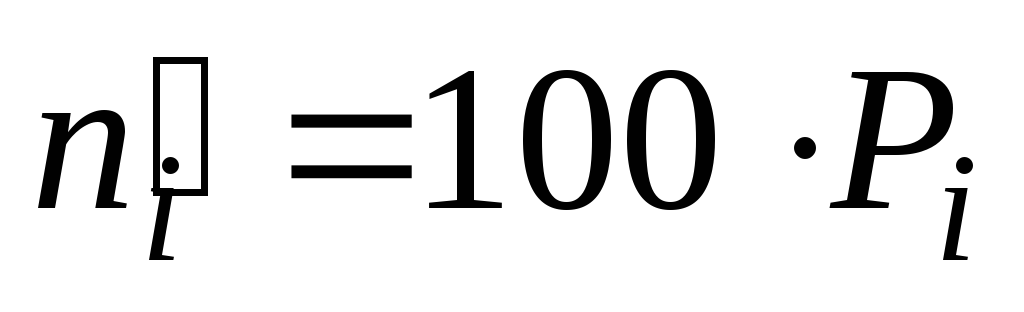
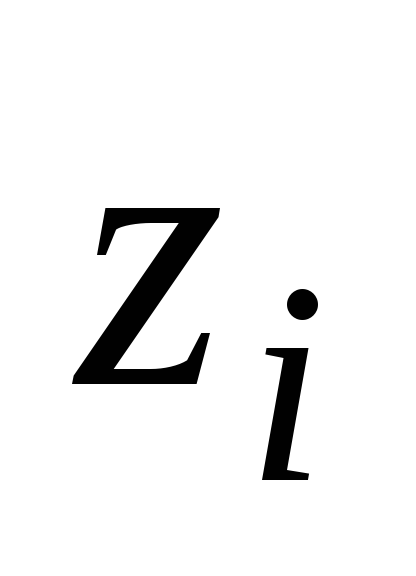
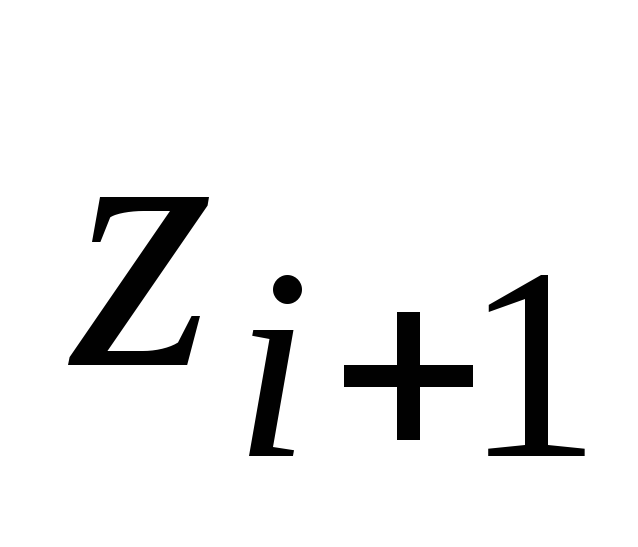
1
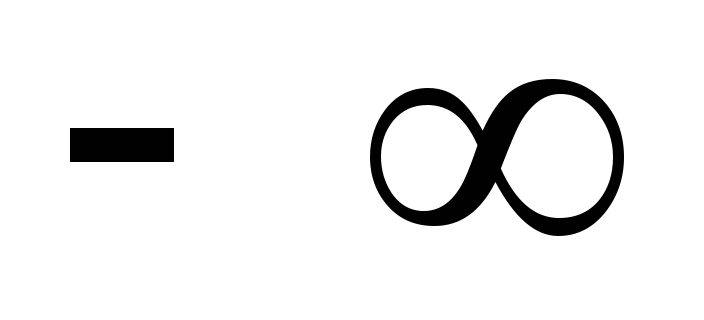
-1,31
-0,5000
-0,4049
0,0951
9,51
2
-1,31
-1,02
-0,4049
-0,3461
0,0588
5,88
3
-1,02
-0,41
-0,3461
-0,1591
0,1870
18,70
4
-0,41
0,21
-0,1591
0,0832
0,2423
24,23
5
0,21
0,82
0,0832
0,2939
0,2107
21,07
6
0,82
1,44
0,2939
0,4251
0,1312
13,12
7
1,44
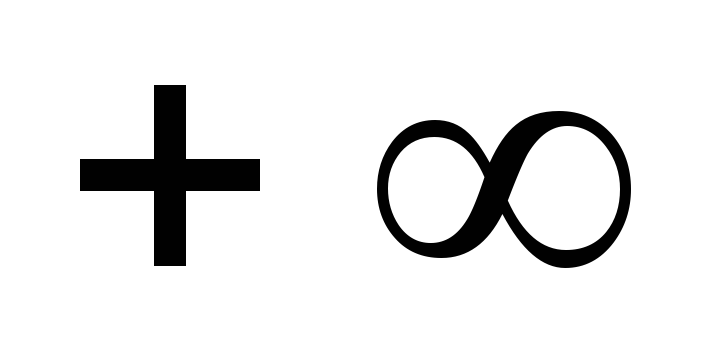
0,4251
0,5000
0,0749
7,49
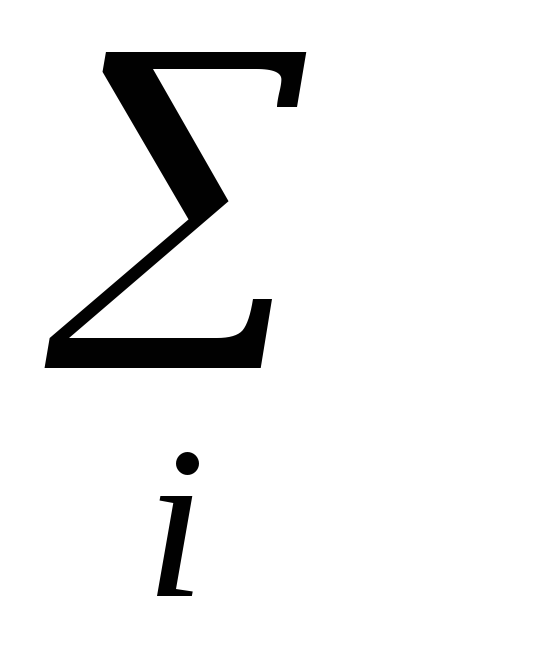
–
–
–
–
1
100
Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу (табл. 5). Последние два столбца служат для контроля вычислений по формуле:
![]()
Таблица 5
-
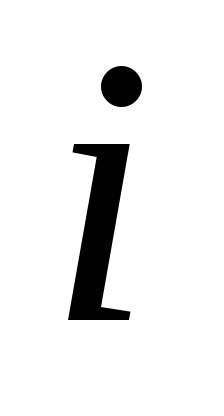



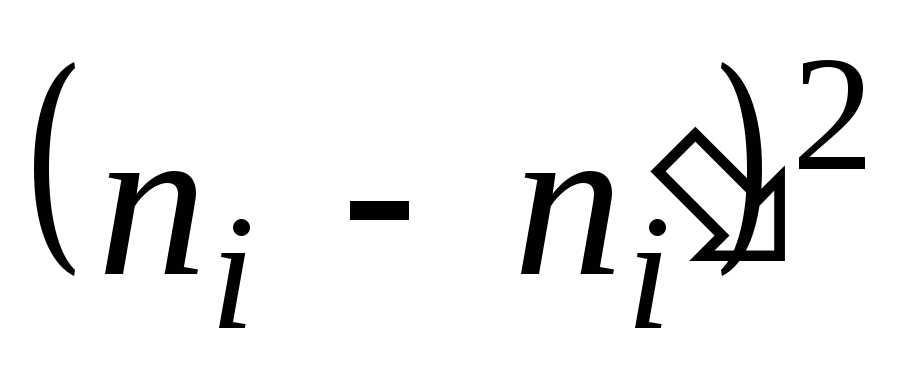
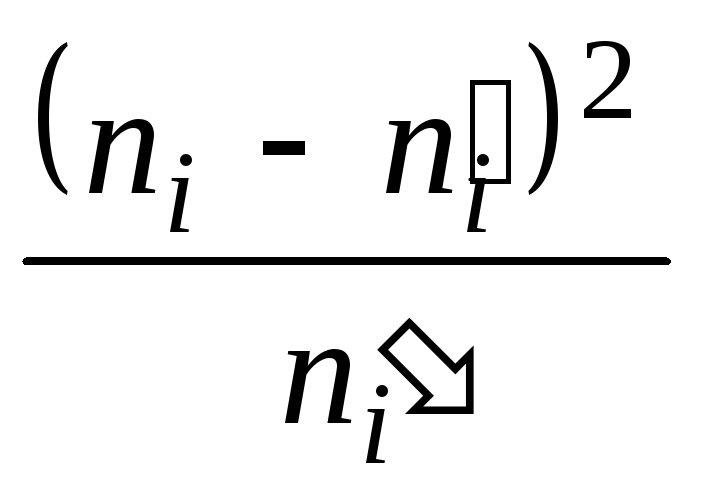
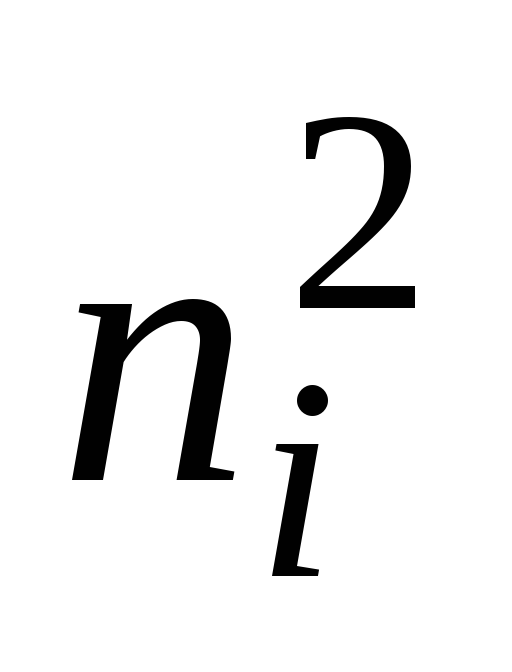
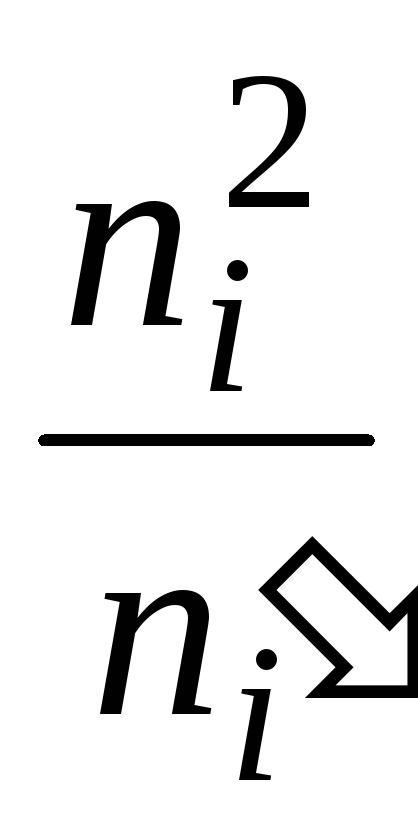
1
7
9,51
-2,51
6,3001
0,6625
49
5,1525
2
13
5,88
7,12
50,6944
8,6215
169
28,7415
3
12
18,70
-6,70
44,89
2,4005
144
7,7005
4
22
24,23
-2,23
4,9729
0,2052
484
19,9752
5
25
21,07
3,93
15,4449
0,7330
625
29,6630
6
14
13,12
0,88
0,7744
0,0590
196
14,9390
7
7
7,49
-0,49
0,2401
0,0321
49
6,5421

100
100
–
–
 12,7138
12,7138–
112,7138
Контроль:
 .
.
По таблице критических точек распределения
![]() (см. прил. 3), уровню
значимости
(см. прил. 3), уровню
значимости
![]() и числу степеней свободы
и числу степеней свободы
![]() (
(![]() – число интервалов) находим:
– число интервалов) находим:
![]() .
.
Так как
![]() ,
то гипотеза
,
то гипотеза
![]() о нормальном распределении
генеральной совокупности принимается.
о нормальном распределении
генеральной совокупности принимается.
6).
Если случайная величина
![]() генеральной совокупности распределена
нормально, то с надежностью
генеральной совокупности распределена
нормально, то с надежностью
![]() можно утверждать, что математическое
ожидание
можно утверждать, что математическое
ожидание
![]() случайной
величины
случайной
величины
![]() покрывается доверительным интервалом
покрывается доверительным интервалом
![]() ,
где
,
где
![]() – точность оценки.
Значение
– точность оценки.
Значение
![]() определяется из условия
определяется из условия
![]() ,
т.е.
,
т.е.
![]() .
.
В нашем случае:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Из прил.1 находим
.
Из прил.1 находим
![]() ,
,
![]() .
Доверительным
интервалом для
.
Доверительным
интервалом для
![]() будет
будет
![]() .
Доверительный интервал, покрывающий
среднее квадратичное отклонение
.
Доверительный интервал, покрывающий
среднее квадратичное отклонение
![]() с заданной надежностью
с заданной надежностью
![]() :
:
![]() ,
где
,
где
![]() находится по данным
находится по данным
![]() и
и
![]() из прил. 2. При
из прил. 2. При
![]() и
и
![]() имеем:
имеем:
![]() .
Доверительным интервалом для
.
Доверительным интервалом для
![]() будет
будет
![]() .
.
