Постановка задачи

Вариант контрольной работы включает пять заданий по следующим темам дисциплины:

1. Построение коммуникационной сети;

2. Определение кратчайшего пути;

3. Определение максимального потока;

4. Задача «о назначениях».

Методические указания

При выполнении контрольной работы необходимо привести все промежуточные вычисления в виде рисунков с объяснением всех выполняемых действий.

Рисунки в заданиях 1 – 4 должны быть выполнены аккуратно, с использованием необходимых инструментов.

Теоретические основы

Большое количество практических задач формулируются как задачи поиска фрагментов графа или каких-то его характеристик, причем существует множество вариантов решения. Каждое решение оценивается числом, и среди множества решений нужно найти такое, для которого оценка имеет экстремальное значение – минимальное или максимальное. Чаще всего в качестве оценок используется сумма весов дуг или ребер, входящих в решение, – тогда оценка называется аддитивной, или произведение весов – тогда говорят о мультипликативной оценке. Наиболее часто ограничиваются случаем, когда веса дуг являются неотрицательными целыми числами.

1. ПОСТРОЕНИЕ КОММУНИКАЦИОННОЙ СЕТИ

МИНИМАЛЬНОЙ ДЛИНЫ

Коммуникационная сеть минимальной длины (или дерево кратчайших расстояний) – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети, т.е. возможность попасть из любого узла в любой другой узел.

Алгоритм:

1. Начать с любого узла и соединить его с ближайшим узлом. Считаем, что эти узлы связанные, а все другие несвязанные.

2. Определить несвязанный узел, ближайший к одному из связанных узлов. Если таких «ближайших» узлов несколько, то выбрать любой. Добавить этот узел к связанным. И т.д., до тех пор, пока есть несвязанные узлы.

Пример. Университет устанавливает компьютерную систему электронной почты, которая позволит передавать сообщения между деканами восьми факультетов. Сеть возможных электронных связей между деканатами показана ниже. Протяженность коммуникаций в километрах отмечена на дугах.

Необходимо предложить проект системы связи, которая позволит всем восьми деканам обеспечить доступ к системе электронной почты. Решение должно обеспечить минимальную возможную общую длину коммуникаций.

Начнем с узла 1. Ближайший к нему узел – это узел 2 на расстоянии 2. Считаем, что узлы 1, 2 – связанные, и выделим эту связь.

Ближайшие несвязные узлы к связным узлам 1 и 2 – это узлы 3 и 6. Выбираем любой из них, например, узел 3. Ребро 1-3 выделяем и считаем узел 3 связанным.

Далее ищем ближайший несвязанный узел к узлам 1, 2, 3. Это узел 7 (ближайший к узлу 3).

Ближайший несвязанный узел к узлам 1, 2, 3, 7 – узел 5 (ближайший к узлу 7).

Далее аналогично. В результате получим минимальное дерево.

Его длина равна сумме расстояний на дугах 2+3+1+1+2+0,5+1=10,5 (км).

2. ЗАДАЧА ОПРЕДЕЛЕНИЯ КРАТЧАЙШЕГО ПУТИ

1. Метод присвоения меток

Задача состоит в том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до любой другой вершины.

Пример: Узел 7 – склад, остальные узлы – строительные площадки компании. Показатели на дугах – расстояния в километрах.

Надо найти кратчайшие расстояния от склада до каждой строительной площадки.

Каждому узлу приписывают метку из двух чисел:

• первое число – минимальное расстояние от узла 7 до данного узла,

• второе – номер предыдущего узла на пути от узла 7 к данному узлу.

Помеченным называют узел, для которого определен путь от узла 7. Иначе узел – непомеченный.

Если кратчайшее расстояние от узла 7 до данного узла определено, то соответствующая метка постоянная и обозначается в круглых скобках. Остальные метки временные и обозначаются в квадратных скобках. Узлы с постоянными метками закрашиваем.

Узлу 7 присваиваем метку (0, S), где 0 – расстояние от узла 7, S – обозначение стартового узла.

Узел 7 связан с узлами 2, 4 и 6. Им присваиваем соответствующие метки – [17, 7], [5, 7], [6, 7].

После выполнения этой операции выполняют два шага:

• находят участок минимальной длины и соответствующую временную метку делают постоянной;

• узел, которому соответствует данная постоянная метка становится новым стартом.

Метка с наименьшим расстоянием [5, 7] соответствует узлу 4. Этот узел объявляем помеченным и заменяем скобки у метки.

Узел 4 связан непосредственно с узлами 2 и 5 без постоянных меток. Временная метка узла 5 равна [5+4, 4]=[9, 4], а у узла 2 – [5+6, 4]= [11, 4]. Т.к. узел 2 уже имеет временную метку [17, 7], то из двух меток выбираем ту, в которой расстояние меньше, т.е. [11, 4].

Из всех временных меток [11, 4], [9, 4], [6, 7] выбираем метку с наименьшим первым числом – [6, 7]. Она становится постоянной и очередной шаг начинаем с узла 6.

Этот узел связан только с узлом 5 без постоянной метки. Временная метка узла 5 равна [6+2, 6]=[8, 6]. Эта метка имеет меньшее первое число, чем предыдущая, поэтому узлу 5 приписываем новую временную метку [8, 6].

Из всех временных меток [11, 4], [8, 6] метку с наименьшим первым числом [8, 6] объявляем постоянной и следующий шаг начинаем с соответствующего ей узла 5.

Узел 5 связан только с одним узлом без постоянной метки – узлом 3. Временная метка узла 3 равна [8+4, 5]=[12, 5].

Из всех временных меток [11, 4], [12, 5] метку с наименьшим первым числом [11, 4] объявляем постоянной и следующий шаг начинаем с соответствующего ей узла 2.

Узел 2 связан с узлами и 1 и 3 без постоянных меток. Временная метка узла 1 равна [11+15, 2]=[26, 2], а узла 3 – [11+3, 2]=[14, 2]. Т.к. узел 3 уже помечен меткой с меньшим первым числом, то метку не меняем.

Из временных меток [26, 2], [12, 5] метка с наименьшим первым числом [12, 5] становится постоянной и следующий шаг начинаем с соответствующего ей узла 3.

Метку узла 1 меняем на (12+10, 3)=(22, 3).

Всем узлам приписаны постоянные метки. Действие алгоритма прекращается.

Первое число метки у каждой вершины – это длина кратчайшего пути от узла 7 до данной вершины. Чтобы восстановить кратчайший путь от узла 7 до какой-то вершины, нужно из этой вершины перейти в соседнюю (ее номер – второе число метки) и т.д. до вершины 7.

Определим кратчайшие расстояния от склада до каждой строительной площадки.

Для строительной площадки 1: метка узла 1 – (22, 3), следовательно, длина кратчайшего пути от узла 7 до узла 1 равна 22. Чтобы определить путь, смотрим второе число метки: из узла 1 идем в узел 3. Метка узла 3 – (12, 5), следовательно, идем в узел 5. Метка узла 5 – (8, 6), следовательно, идем в узел 6. Метка узла 6 – (6, 7), следовательно, идем в узел 7. Т.о., кратчайший путь 1-3-5-6-7.

Для строительной площадки 2: длина кратчайшего пути до склада равна 11; кратчайший путь 2-4-7.

Для строительной площадки 3: длина кратчайшего пути до склада равна 12; кратчайший путь 3-5-6-7.

Для строительной площадки 4: длина кратчайшего пути до склада равна 5; кратчайший путь 4-7.

Для строительной площадки 5: длина кратчайшего пути до склада равна 8; кратчайший путь 5-6-7.

Для строительной площадки 6: длина кратчайшего пути до склада равна 6; кратчайший путь 6-7.

2. Задача о кратчайшем пути между двумя пунктами

Известна схема дорог. Требуется перевезти груз из одного пункта в другой по маршруту минимальной длины.

Двигаясь от конечного пункта к начальному пункту, каждой вершине припишем число по определенным правилам. Конечной вершине присвоим число 0. Если i-я вершина в направлении от начального пункта к конечному пункту непосредственно соединена с вершинами j₁, …, j_k, которым приписаны числа r(j₁), …, r(j_k), то вершине i приписывается число , где – длина ребра.

Пусть этот минимум достигается для вершины j_m. Тогда ребро (i, j_m) отмечаем жирной стрелкой от i к j_m. Если таких j_m несколько, то на этом шаге будет несколько выделенных ребер.

Число, приписанное начальному пункту, равно минимальной длине искомого маршрута. Для получения оптимального маршрута двигаются по выделенным стрелкам от начального пункта к конечному.

Пример. Найти маршрут минимальной длины от пункта 1 к пункту 11.

Для вершины 11: r(11)=0.

Для вершины 10: r(10)=min(r(11)+l(10,11))=min(0+4)=4. Выделяем ребро (10,11).

Для вершины 9: r(9)=min(r(11)+l(9,11))=min(0+5)=5. Выделяем ребро (9,11).

Для вершины 8: r(8)=min(r(11)+l(8,11))=min(0+5)=5. Выделяем ребро (8,11).

Для вершины 7:

. Выделяем ребро (7,9).

Для вершины 6:

. Выделяем ребро (6,10).

Для вершины 5:

. Выделяем ребро (5,8).

Для вершины 4:

. Выделяем ребро (4,6).

Для вершины 3:

. Выделяем ребро (3,7).

Для вершины 2:

. Выделяем ребро (2,5).

Для вершины 1:

. Выделяем ребро (1,4).

Длина кратчайшего пути равна 14. Двигаясь от начальной вершины к конечной по выделенным ребрам, получим кратчайший путь 1-4-6-10-11.

3. ЗАДАЧА ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПОТОКА

Рассматривается сеть с одним узлом входа (источник) и одним узлом выхода (сток). Определить максимальную величину потока (количество машин, сообщений, жидкости и т.д.), который может войти в сетевую систему и выйти из нее в заданный период времени. Предполагается, что поток, вытекающий из узла, равен потоку, втекающему в узел.

Пропускная способность (или мощность) дуги – верхнее ограничение на поток в этой дуге. Например, автомобильные трассы ограничивают число автомобилей в транспортной системе, величина трубопроводов ограничивает количество нефти в системе ее распределения.

Мощность потока может зависеть от его направления.

Это условное обозначение означает, что мощность потока от узла 1 к узлу 2 равна 6, а мощность потока от узла 2 к узлу 1 равна 0, т.е. это «улица с односторонним движением».

Условное обозначение

означает, что мощность потока в каждом направлении равна 2.

Алгоритм:

Полагаем искомую величину максимального потока равной нулю.

Шаг 1. Найти какой-нибудь путь от источника до стока, который образован дугами, каждая из которых имеет в направлении потока ненулевую мощность. Если такого пути нет, то оптимальное решение найдено.

Шаг 2. Найти наименьшее значение мощности дуги P_f на выбранном пути шага 1. Увеличить поток через сеть на величину P_f.

Шаг 3. На пути из шага 1 сократить на P_f мощности потоков на всех дугах в направлении потока и увеличить на P_f мощности потоков на всех дугах, в обратном направлении. Перейти к шагу 1.

Пример. Система автодорог «Север-Юг», проходящих через Псковскую область, может обеспечить пропускные способности, показанные на схеме (тыс. автомашин в час).

Определить максимальный поток через эту систему (тыс. автомашин в час).

Искомую величину максимального потока положим равной нулю.

Итерация 1. Выберем путь 1-3-6.

P_f = min{6, 2}=2. Поэтому мощности потоков на пути 1-3-6 в направлении потока (а именно, 6 и 2) уменьшаем на величину P_f =2, а мощности потоков в обратном направлении на пути 1-3-6 (0 и 0) увеличиваем на P_f =2. Общий поток станет 0+2=2.

Получим:

Итерация 2. Выберем путь 1-4-6.

P_f = min{3, 3}=3. Все потоки на пути 1-4-6 в направлении общего потока (3 и 3) уменьшаем на P_f =3, а все потоки на этом пути в обратном направлении (0 и 0) увеличиваем на P_f =3. Общий поток увеличиваем на P_f =3 (2+3=5).

Получим:

Итерация 3. Выбираем путь 1-2-5-6.

P_f = min{2, 4, 6}=2. Все потоки на пути 1-2-5-6 в направлении общего потока (2, 4, 6) уменьшаем на P_f =2, а все потоки на этом пути в обратном направлении (0, 4, 0) увеличиваем на P_f =2. Общий поток увеличиваем на P_f =2 (5+2=7).

Получим:

Итерация 4. Выбираем путь 1-3-4-5-6.

P_f = min{4, 3, 1, 4}=1. Все потоки на пути 1-3-4-5-6 в направлении общего потока (4, 3, 1, 4) уменьшаем на P_f =1, а все потоки на этом пути в обратном направлении (2, 3, 1, 2) увеличиваем на P_f =1. Общий поток увеличиваем на P_f =1 (7+1=8).

Получим:

Итерация 5. Выбираем путь 1-3-4-2-5-6.

P_f = min{3, 2, 1, 2, 3}=1. Все потоки на пути 1-3-4-2-5-6 в направлении общего потока (3, 2, 1, 2, 3) уменьшаем на P_f =1, а все потоки на этом пути в обратном направлении (3, 4, 1, 6, 3) увеличиваем на P_f =1. Общий поток увеличиваем на P_f =1 (8+1=9).

Получим:

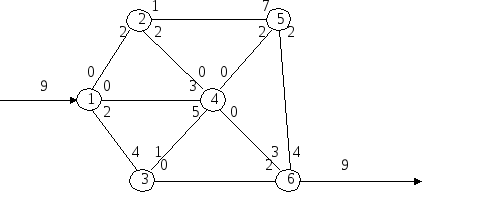
Больше не существует путей из узла 1 в узел 6 с мощностью, превышающей нуль на всем пути. Следовательно, 9 тыс. – это максимальный поток через сеть.

Определим величину и направление потока (тыс. автомашин в час) на каждой дуге. Направление потоков соответствует выбранным путям. Поток проходит по дуге с величиной, равной разнице между первоначальной и конечной мощностями потока:

• дуга 1-2: первоначальная мощность равна 2 (в исходном графе), конечная – 0 (в последнем графе), следовательно, в направлении от узла 1 к узлу 2 поток имеет мощность 2-0=2;

• дуга 1-3: 6-2=4; – дуга 4-2: 1-0=1;

• дуга 1-4: 3-0=3; – дуга 4-5: 1-0=1;

• дуга 2-5: 4-1=3; – дуга 4-6: 3-0=3;

• дуга 3-4: 3-1=2; – дуга 5-6: 6-2=4.

• дуга 3-6: 2-0=2;

В итоге получим граф, на котором указаны направления и мощности потоков по каждой дуге:

4. ЗАДАЧА «О НАЗНАЧЕНИЯХ»

Пусть есть N работников и N рабочих мест (работ). Известно время выполнения каждым работником каждой из работ. Необходимо так распределить работников по рабочим местам, чтобы каждый работник выполнял одну работу, каждая работа выполнялась одним работником при минимальном времени выполнения работ. Классическим примером этой задачи может быть распределение спортсменов по этапам эстафеты.

В задаче о назначениях целевая функция может как минимизироваться (время, расстояние, затраты), так максимизироваться (эффективность, производительность, прибыль).

Задача решается венгерским методом.

Алгоритм венгерского метода при минимизации целевой функции:

1. В каждой строке матрицы задачи находят минимальный элемент и вычитают его из всех элементов строки.

2. В каждом столбце полученной матрицы находят минимальный элемент и вычитают его из всех элементов столбца.

3. Находят строку с одним нулем. Этот нуль заключается в квадрат и называется отмеченным. В столбце, где находится отмеченный нуль, все остальные нули зачеркиваются и в дальнейшем не рассматриваются. Этот шаг продолжают, пока возможно.

4. Находим столбец с одним нулем и этот нуль отмечаем. В строке, где находится отмеченный нуль, все остальные нули зачеркиваются. Этот шаг продолжают, пока возможно.

5. Если после шагов 3 и 4 еще есть неотмеченные нули, то отмечаем любой из них, а в строке и в столбце, где находится этот отмеченный нуль, все остальные нули зачеркиваем.

6. Если каждая строка и каждый столбец матрицы содержит ровно один отмеченный нуль, то получено оптимальное решение. Каждый ил отмеченных нулей указывает прикрепление работника к работе (поставщика к потребителю).

7. Если решение не оптимальное, проводят минимальное число пересекающихся горизонтальных и вертикальных прямых через все нули. Среди не зачеркнутых этими прямыми чисел находят минимум. Этот минимум вычитают из всех незачеркнутых чисел и прибавляют ко всем числам на пересечении прямых. Переходят на шаг 3 данного алгоритма.

Пример. Существуют четыре базы А₁, А₂, А₃, А₄ и четыре торговые точки В₁, В₂, В₃, В₄. Расстояния от баз до торговых точек заданы матрицей:

Нужно так прикрепить базы к торговым точкам, чтобы суммарное расстояние было минимальным.

Шаг 1. Находим минимум в 1-ой строке (это 5) и вычитаем его из всех элементов 1-ой строки. Аналогично с остальными строками.

Получим матрицу:

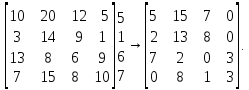
Шаг 2. В полученной матрице находим минимумы в каждом столбце (0, 2, 0, 0 соответственно) и вычитаем их из всех элементов соответствующего столбца.

Получим матрицу:

Шаг 3. В 1-ой строке один нуль. Отметим его. Он находится в 4-м столбце. Поэтому в 4-м столбце зачеркиваем все остальные нули.

Получим матрицу:

Аналогично поступаем с 4-ой строкой. Больше нет строк с одним нулем. Зато есть столбцы с одним нулем.

Шаг 4. 2-й столбец содержит один нуль, который мы и отметим. Этот нуль находится в 3-ей строке. Поэтому в 3-ей строке зачеркиваем все нули.

Получим матрицу:

Больше нулей нет. Полученное распределение не является оптимальным, так как во 2-ой строке нет отмеченных нулей.

Шаг 7. Проведем минимальное число пересекающихся горизонтальных и вертикальных прямых через все нули. Можно применить любой способ проведения прямых. В данном случае достаточно трех прямых.

Среди не зачеркнутых этими прямыми чисел находим минимум:

.

Этот минимум вычитается из всех незачеркнутых чисел и прибавляется ко всем числам на пересечении прямых (3, 3). Получим матрицу:

К этой матрице применим алгоритм, начиная с шага 3.

Полученное решение не является оптимальным, так как в 3-м столбце нет отмеченных нулей. Проводим прямые.

Этот минимум вычитается из всех незачеркнутых чисел и прибавляется ко всем числам на пересечении прямых (7, 5). Получим матрицу:

К этой матрице применим алгоритм, начиная с шага 3.

В каждой строке и в каждом столбце матрицы ровно один отмеченный нуль. Это оптимальное распределение. Возможно, оно не является единственным.

В итоге, А₁ прикрепляется к В₄, А₂ – к В₁, А₃ – к В₂, А₄ – к В₃. Чтобы найти суммарное расстояние, нужно сложить числа, которые расположены в исходной матрице на месте отмеченных нулей: S = 5+3+8+8 = 24.

При максимизации целевой функции необходимо все элементы исходной матрицы умножить на (-1), что сведет задачу к задаче минимизации. Затем к полученной матрице применить тот же алгоритм.