Теория Информации / 05 Энтропия, количество информации

1

5. ЭНТРОПИЯ, КОЛИЧЕСТВО ИНФОРМАЦИИ

Введение Понятие энтропии возникло в связи с необходимостью ввести

численную характеристику неопределенности случайного объекта на некотором этапе его рассмотрения. Все, что мы можем сказать априори о поведении случайного объекта, это указать множество его состояний и указать распределение вероятностей по элементам этого множества. Обратим внимание на то, что различные распределения с различной неопределенностью характеризуют, какое из возможных состояний объекта должно реализоваться. Например, пусть некоторый объект имеет два возможных состояния, А1 и А2; пусть при одних условиях распределение вероятностей характеризуется числами р(А1) = 0,99, р(А2) = 0,01; а в другом случае – р(А1) = р(А2) = 0,5. Очевидно, что в первом случае результатом опыта «почти наверняка» будет реализация состояния А1, во втором же случае неопределенность так велика, что естественно воздержаться от всяких прогнозов. Мы приходим к необходимости количественного описания неопределенности заданного распределения вероятностей. Понятие «неопределенность» естественно связывается с формой распределения, но не с множеством конкретных значений случайной величины. Поэтому первое требование к мере неопределенности состоит в том, что она должна быть функционалом, т.е. функцией от функции распределения., и не зависеть от конкретных значений случайной величины. Кроме того, к мере неопределенности должен быть предъявлен еще ряд требований, таких как непрерывность относительно аргументов, наличие максимума и дополнительные требования, которые более подробно будут рассмотрены ниже. Важно подчеркнуть, что такой комплекс разумно выдвинутых требований к мере неопределенности допускает единственную форму функционала, который по ряду причин, подлежащих отдельному обсуждению, и назван энтропией случайного объекта.

Термин «энтропия» был введен в 1865 году Р.Клаузиусом для характеристики процессов превращения энергии (дословно, с греческого, энтропия означает превращение, обращение). В 1877 году Л.Больцман дал этому понятию статистическое толкование и сформулировал с его помощью второй закон термодинамики. В последующем понятие энтропии стали широко применять в статистической физике и математике.

В 1948 году понятие энтропии использовал К.Шеннон в качестве основы информационной метрики для абстрактной модели системы связи в созданной им статистической теории информации. В абстрактной модели, являющейся объектом анализа в статистической теории информации, любое сообщение представляет собой результат выбора из некоторого ансамбля возможных сообщений, ансамбля, которому присуща некоторая степень неопределенности; если же состояние ансамбля известно, то нет необходимости в сообщении. Совершенно очевидно, что степень неопределенности ансамбля зависит от числа событий и их вероятностей,

2

при этом под ансамблм понимается поле случайных несовместных событий из некоторого множества с известным распределением вероятностей, составляющих в сумме единицу. В качестве меры априорной неопределенности такого ансамбля событий (и, следовательно, его информативности) в статистической теории информации принята величина энтропии.

5.1. Энтропия и ее свойства

Изучение информационных характеристик сообщений, сигналов и их свойств целесообразно начать с определения и анализа дискретных ансамблей и источников. Будем рассматривать множество сообщений А = {а1, ..., аK}, состоящее из конечного числа К элементов аK. (Принято обозначать сами множества прописными буквами, а строчными — элементы этих множеств.) Предположим, что на множестве А задано распределение р(а), где каждому элементу аK из А соответствует значение вероятности p(aK ) ≥ 0, ∑ p(aK ) = 1. Множество А с заданным на нем распределением р(а)

K

называют дискретным ансамблем сообщений, обозначая его {А, р(а)}.

Рассмотрим теперь два множества сообщений А и В, содержащих конечное число элементов К и N соответственно. Будем называть множество,

элементы которого представляют все	возможные упорядоченные пары
(ai ,bj ),i [1, K], j [1, N], произведением А	и В, обозначая его как АВ. Из

определения следует, что в общем случае АВ и ВА — различные множества. Если множества А и В совпадают, используется обозначение А2.

Для множества АВ с заданным совместным распределением р(а,b) определен дискретный ансамбль {АВ, р(а,b)}. При определении АВ задаются еще два ансамбля А и В (на основании свойства согласованности

распределений	дискретной	случайной	величины	p(a) = ∑ p(a,b),
				B

p(b) = ∑ p(a,b) р(а)). А и В называют ансамблями статистически независимых

A

сообщений, если p(a,b) = p(a) p(b).

При наличии статистической зависимости сообщений величина, определяемая соотношением p(bj | ai ) = p(ai ,bj ) / p(ai ) (предполагается, что

p(ai ) ≠ 0 ), называется условной вероятностью сообщения bj при условии, что сообщение аi фиксировано (задано). Известно, что множество условных вероятностей относительно фиксированного сообщения аi, получаемое при переборе всех значений индекса j, удовлетворяет общему определению распределения вероятностей. Это есть условное распределение на множестве В относительно заданного сообщения аi. Аналогичным образом задается условное распределение на множестве А относительно сообщения bj. Отсюда следует, что задание ансамбля {АВ, р(а,b)} определяет еще два «условных» ансамбля сообщений {A, p(a | b)} и {B, p(b | a)}. При определении условных ансамблей предполагается, что в исходных ансамблях не существует сообщений с нулевой вероятностью.

3

Дальнейшее обобщение понятия ансамбля сообщений связывают с произведением A1, A2 ,..., An , представляющим собой множество всех последовательностей a(1) ,a(2) ,...,a(n) длины п, таких, что первый элемент принадлежит множеству A1 и т.д. (надстрочный индекс обозначает номер элемента в последовательности). При этом образуется ансамбль,

обозначаемый	[A ,..., A , p(a(1)		,a(2)	,...,a(n) )]. При совпадении	всех	элементов
	1	n
произведения	A , A ,..., A используется обозначение Ап.				Таким	образом,
	1 2	n

представляется множество всех последовательностей длины п, образованных из элементов множества А. Очевидно, что все закономерности, отмеченные при рассмотрении частного случая n = 2, при необходимости могут быть обобщены на произведение п ансамблей.

Энтропия ансамбля сообщений. Рассмотрим источник дискретных сообщений, характеризуемый ансамблем сообщений {A, p(a)}, у которого

р(аk) ≠ 0.

Для неслучайной характеристики ансамбля сообщений вводят понятие

энтропии. Математическое ожидание случайной величины i[a), определенной на ансамбле {А,р[а)}, называется энтропией (Н) этого ансамбля:

H(A)= M{i(a)}= ∑i(a)p(a)= −∑ p(a)log p(a).

(5.1)

AA

Величину i(ak), определяемую соотношением
i(ak )= −log p(ak ), k = 1,...,K	(5.2)

называют количеством собственной информации (или собственно информацией) в сообщении ak A. Собственная информация, определенная (5.2) как функция случайного события, является случайной величиной.

Понятие энтропии в теории информации является основополагающим. Количество информации, которое может быть получено от источника, оказывается тем большим, чем большей энтропией обладает источник. Количество информации трактуется как мера неопределенности, связанная с ожидаемым от источника сообщением. Сообщение является тем более неопределенным (неожиданным), чем оно оказывается менее вероятным. В общем случае с увеличением числа возможных состояний и уменьшением их вероятности энтропия источника возрастает. Чем выше энтропия источника, тем сложнее передать сообщение от этого источника по каналу связи (хотя бы с точки зрения энергетических затрат).

Рассмотрим основные свойства энтропии.

1.	Энтропия всякого дискретного ансамбля неотрицательна:
Н(А) ^ 0.	Равенство нулю имеет место в том и только в том случае, когда в

ансамбле существует сообщение, вероятность которого 1; при этом вероятности остальных сообщений равны 0. Неотрицательность следует из того, что собственная информация каждого сообщения ансамбля неотрицательна.

2.Пусть К — число сообщений в ансамбле. Тогда

	4
H(A)≤ log K.	(5.3)

Равенство имеет место только в том случае, когда все сообщения ансамбля независимы и равновероятны.

Простое доказательство сделанного утверждения основано на сле-

	дующем неравенстве для натурального логарифма:
	ln x ≤ x – 1,			(5.4)
	где равенство имеет место только при х = 1.
	Рассмотрим разность
	H(A)− log K = −∑ p(a)log p(a)− log K =
	A
	= −∑ p(a)[log p(a)+ log K])= loge∑ p(a)ln		1	.
			Kp(a)
	A	A

Используя теперь неравенство (5.4), получим

Отсюда следует неравенство в (5.3). Равенство имеет место только тогда, когда р(а) = 1/К для всех а А (равенство в (5.4) справедливо только при х = 1).

Пример. Пусть X = {x1,x2} —двоичный ансамбль и p(x1) = р, р(x2) = 1- р — вероятности его сообщений. В этом случае энтропия является функцией одной переменной р:

Н(Х) = -рlog p - (1 - р) log(l - р).

H	дв.ед
	сообщ.
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0	P

Рис. 5.1. График зависимости Н (x) в функции р

График этой функции представлен на рис. 5.1. В точках р = 0 и р = 1 она не определена и в соответствии с предыдущим замечанием доопределяется до нуля. Поведение Н(Х) как функции от р облегчается вычислением про-

5

изводных по параметру р.

3. Энтропия обладает свойством аддитивности.

Пусть А и В — статистически независимые ансамбли, характеризуемые энтропиями Н(А) и Н(В). Учитывая, что M[i(a,b)] = Н(А,В) есть энтропия ансамбля {АВ,р(а,b)}, получим

H(A,B)= M[i(ai ,bj )]= M[i(ai )+ i(bj )]= H(A)+ H(B).

Свойство аддитивности энтропии приводит к тому, что энтропия укрупненного ансамбля в определенной мере превосходит энтропию исходного источника.

5.2. Условная информация. Условная энтропия. Совместная энтропия

Рассмотрим теперь {АВ,р(а,b)} —два совместно заданных ансамбля {А,р(а)} и {В,р(b)}. На каждом из множеств А и В могут быть определены условные распределения. Зафиксируем некоторое сообщение b и рассмотрим условное распределение на множестве А. Условное распределение на А относительно фиксированного значения b удовлетворяет всем свойствам безусловных распределений и, следовательно, при задании АВ задаются также условные ансамбли {А | b,р(а | b)} и {В | а,р(b \ а)}; предполагается, что р(а) и р{b) не равны 0. Для каждого сообщения а в ансамбле {А \ b,p(a \ b)} определена собственная информация

i(a		b)= −log p(a		b),	(5.6)

называемая условной собственной информацией сообщения а при фиксированном сообщении b. Математическое ожидание условной информации

называется условной энтропией ансамбля А относительно сообщения b. Математическое ожидание Н(А\В) случайной величины Н(А\b),

определенной на ансамбле {В,р(b)}, называется условной энтропией ансамбля А относительно ансамбля В:

(5.7) Таким же образом убеждаемся в справедливости равенства

(5.7а) Математическое ожидание собственной информации пары сообщений

i{а,b) = — log p(a,6) представляет собой энтропию (совместную энтропию) ансамбля АВ:

(5.8) Продолжим рассмотрение свойств энтропии, условной и совместной

энтропии.

6

1. Из определения условной вероятности p(a,b) = p{a)p(b \ а) следует,

что

и аналогично Н(АВ) = Н(А | В) + Н(В). Эти свойства также называются свойствами аддитивности энтропии.

2. Условная энтропия не превосходит безусловной энтропии того же ансамбля: Н(А \ В) ≤ Н{А), причем равенство имеет место в том и только в том случае, когда ансамбли А и В статистически независимы. Доказательство проводится аналогично доказательству справедливости неравенства (5.3) с использованием неравенства (5.4) для логарифма:

Равенство выполняется в том и только в том случае, когда р(а, 6) = =

р{а)р{b) для всех а и b, т.е. когда ансамбли А и В статистически независимы. Рассмотрим частный случай, когда В = А, так что a = a(1), b = а(2).

Тогда на основании свойств 1 и 2 можно сделать вывод, что совместная энтропия Н(А, А) = Н(А2) имеет наибольшее значение, равное 2Н(А), когда сообщения в ансамбле А не имеют статистической связи.

3. Из свойства 2 условной энтропии вытекает следующая закономерность. Зададим на ансамбле {А,р(а)} отображение φ(a) множества А в множество X, определяющее ансамбль {Х,р(х)} следующим образом:

p(x)= ∑ p(a).

a:ϕ (a)=x

Тогда Н(Х) ≤ Н(А); знак равенства имеет место только в том случае, когда отображение φ(a) обратимо, т.е. когда каждому элементу х соответствует единственный элемент а. Для доказательства можно воспользоваться равенством р(а, х) = р{а)р{х \ а), где р(х | а) = 1, когда х = φ(a), и р(х \ а) = 0 для остальных х, т.е. когда каждое сообщение ансамбля А однозначно определяет сообщение ансамбля X. Тогда Н(Х \ А) — 0, и из аддитивности и неотрицательности энтропии получим, что

Отсюда следует вывод, что при произвольных отображениях φ{а) энтропия не возрастает. Энтропия не изменяется только тогда, когда Н{А | X) = 0, т.е. когда ансамбль X взаимно однозначно отображает ансамбль А.

4. Для трех совместно заданных ансамблей {ABG,p{a,b,g)} справедливо неравенство Н(А \ BG) ≤ Н{А \ В), которое доказывается аналогично проведенному при рассмотрении свойства 2. Равенство здесь имеет место

7

при статистической независимости ансамблей А и G. Это неравенство легко обобщается на случай п совместно заданных ансамблей. При этом оказывается справедливым утверждение [1], что H(Ai,...,An)≤ ∑ Н(Аi). Знак равенства имеет место в случае статистической независимости сообщений в ансамблях Ai,...,An.

5.3. Энтропия непрерывного источника информации (дифференциальная энтропия)

На практике мы в основном встречаемся с источниками информации, множество возможных состояний которых составляет континуум. Такие источники называют непрерывными источниками информации.

Во многих случаях они преобразуются в дискретные посредством использования устройств дискретизации и квантования. Вместе с тем существует немало и таких систем, в которых информация передается и преобразуется непосредственно в форме непрерывных сигналов. Примерами могут служить системы телефонной связи и телевидения.

Оценка неопределенности выбора для непрерывного источника информации имеет определенную специфику. Во-первых, значения, реализуемые источником, математически отображаются непрерывной случайной величиной. Причем понятие «непрерывность» имеет смысл только для количеств, так что объект с континуумом возможных состояний – это по необходимости количественная случайная величина. Во-вторых, вероятности значений этой случайной величины не могут использоваться для оценки неопределенности, поскольку в данном случае вероятность любого конкретного значения равна нулю.

Естественно, однако, связать неопределенность выбора значения непрерывной случайной величины с плотностью распределения вероятностей (являющейся в общем случае размерной величиной) этих значений.

Понятие энтропии (5.1) обобщено Шенноном на случай непрерывных сообщений x(t). Чтобы не иметь дела с логарифмами размерных величин, введем в рассмотрение безразмерную случайную величину x = x*/x0, где x* - размерная случайная величина, x0 – единица ее измерения. Тогда и плотность вероятности p(x) будет безразмерной функцией.

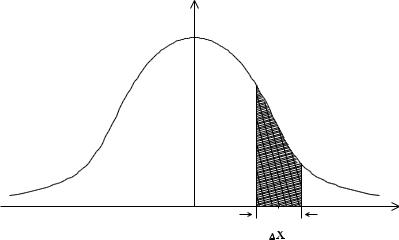
Пусть, например, x(t) приближенно представляется дискретной (с интервалом дискретизации t) последовательностью квантованных отсчетов с шагом квантования х. Тогда в пределах изменения непрерывного сообщения ± хmax будем иметь m = (2xmax / x +1) квантованных уровней. Если, далее плотность вероятности функции x(t) известна (рис. 5.2), то можно определить

вероятность

появления

i-го

уровня

квантованного

значения

xi ,

т.е.

P(

) w(xi )

xi

x. Тогда в соответствии с (5.1) энтропия квантованного сигнала

равна:

−

−

−

w(x

) xlogw(x )+

w(x ) xlog

x

=

H x = −

∑

P xlogP x = −

∑

i

∑

i

i

i

i

i

8

= – ∑w(xi )logw(xi ) x − log x,

i

так как ∑w(xi ) x = 1.

i

w(x)
xi	x
Рис. 6.2. Плотность вероятности функции x(t)

Переходя к пределу при x → 0, получаем, что энтропия на один отсчет непрерывного источника сообщений равна

	∞		1
	~
H(x) = lim [H(x)]= − ∫w(x)logw(x)dx + lim log				.
x→0	−∞	x→0	x

Первое слагаемое правой части выражения называется дифференциальной энтропией непрерывного источника сообщений

h(x)= − ∞∫w(x)logw(x)dx .	(5.9)
−∞

Отличия от энтропии дискретных величин подчеркиваются в названии: благодаря связи h(x) с дифференциальным законом распределения вероятностей, ее называют дифференциальной энтропией; иногда употребляемый термин относительная энтропия указывает на условность, относительность этой характеристики.

Величина (5.9) имеет конечное значение, не зависит от шага квантования, а зависит только от ФПВ w(x). В отличие от энтропии дискретных источников h(x) может принимать положительные, отрицательные и нулевые значения. Величина (5.9) изменяется при изменении масштаба измерения x(t). Что же

касается второго слагаемого, то оно при x → 0 стремится к бесконечности.

−

Энтропия величины x (за счет второго члена) стремится к бесконечности при уменьшении интервала квантования x. Этого, вообще говоря, и следовало ожидать, так как даже в дискретном случае при бесконечном числе состояний энтропия не имеет верхней грани.

Однако в ряде важных задач интересующие нас зависимости, такие как

9

скорость передачи и пропускная способность, определяются разностью энтропии. По этой причине второй член выражения (5.9) часто не учитывают при рассмотрении.

Величина h(x), несмотря на ее относительность, имеет очень важное значение в теории информации.

5.4. Фундаментальное свойство энтропии дискретных эргодических процессов

Мы рассмотрели неопределенность и ее меру – энтропию – для случайных величин и событий. Необходимо теперь сделать следующий шаг – обобщить эти понятия таким образом, чтобы иметь возможность оценивать неопределенность случайных процессов.

Случайный процесс Xt можно рассматривать как множество случайных величин, определенных на множестве значений параметра t (для конкретности считаем, что t является временем). Исходя из этого, неопределенность случайного процесса можно определить как неопределенность всей совокупности случайных величин, образующих процесс Xt. Следует при этом отметить ряд особенностей такого представления.

Во-первых, нецелесообразно оценивать неопределенность случайного процесса на всей оси времени, от -∞ до +∞, так как в общем случае это сразу же приведет к бесконечным величинам. Естественно, возникает вопрос о возможности введения меры средней неопределенности случайного процесса, приходящейся на некоторый интервал времени, в частности – на единичный интервал.

Во-вторых, при вычислении энтропии множества реализаций случайного процесса конечной длины возникаетнеобходимость учета статистической связи между случайными величинами, соответствующими различным значениям параметра t.

Имея в виду эти и другие особенности энтропийного описания непрерывных процессов, обратимся сначала к рассмотрению простого случая

– стационарного процесса с дискретным временем и дискретным конечным множеством возможных состояний в каждый момент времени.

Рассмотрим множество реализаций такого случайного процесса длительностью в п элементов. Если множество возможных состояний каждого элемента насчитывает т состояний, то общее число отличающихся между собой реализаций будет равно тп. Осуществление каждой реализации можно рассматривать как осуществление случайного события из тп возможных событий. Зная распределение вероятностей возможных состояний каждого элемента и характер связей между элементами, можно вычислить вероятность каждой из тп реализаций, р(С). Теперь, в полном соответствии с тем, как это делалось для обычных случайных событий, мы можем вычислить энтропию множества п-членных реализаций:

H = lim Hn ,

10

Hn	= −∑ p(C)log p(C).	(5.10)
	C
Величина Hn, конечно, зависит от того, каково п. Желая образовать
унифицированную	энтропийную характеристику	случайного процесса,

естественно ввести в рассмотрение величину

(5.11)

n→∞ n

если, конечно, указанный предел существует. Величина H будет характеризовать среднюю неопределенность, приходящуюся на один элемент процесса, и может быть названа энтропией процесса.

В [7] доказывается, что для каждого стационарного процесса предел (5.11) действительно существует.

Для каждого из т п событий можно определить его вероятность р(С). На множестве этих событий можно задать любую числовую функцию fn(C),

которая будет, очевидно, случайной величиной. В частности,			такой
случайной величиной будет числовая функция:
fn (C)= −	1	log p(C).
	n

Математическое ожидание этой функции находится обычным образом:

Mfn (C)= ∑ p(C)fn

(C)= −

1

∑ p(C)log p(C).

(5.12)

n

C

C

Отсюда сразу следует, что

1

Hn

M

−

log p(C) =

.

(5.13)

n

n

Поскольку предел lim(Hn / n) существует, то и

n→∞

lim

−

1

log p(C) = H,

(5.14)

n→∞

n

т.е. при п → ∞

математическое ожидание случайной

величины

fn (C)= − 1 log p(C) имеет пределом энтропию случайного процесса Н [7].

n

Это соотношение между Н и Р(С) является одним из проявлений общего свойства дискретных эргодических процессов. Оказывается, что не только математическое ожидание величины fn(C) при п → ∞ имеет пределом Н, но и сама эта величина fn(C) стремится по вероятности к Н при п → ∞.

Другими словами, как бы малы ни были ε > 0 и δ > 0, при достаточно большом п вероятность неравенства fn (C)− H > ε будет меньше, чем δ;

близость fn(C) к Н при больших п является почти достоверным событием. Это фундаментальное свойство эргодических процессов впервые было

обнаружено К. Шенноном [4] на примерах процесса с независимыми элементами и простой марковской цепи. Позднее было доказано, что этим свойством обладают любые эргодические процессы [7].