EO_Lab_rabota_4

4. ЛАБОРАТОРНАЯ РАБОТА

«Дискретные и непрерывные случайные величины»

Оглавление

Цель 1

Дискретные случайные величины 1

Непрерывные случайные величины 3

Биноминальное распределение 5

Распределение Пуассона 7

Геометрическое распределение 7

Гипергеометрическое распределение 9

Нормальное распределение 11

Равномерное распределение 13

Показательное распределение 13

Контрольные задания 13

Цель

Целью лабораторной работы №4 является знакомство с возможностями программы Maple для расчеты распределения случайной величины по условию задачи, по нахождению ее числовых характеристик, таких как математическое ожидание, дисперсия и среднее квадратическое отклонение. .

Дискретные случайные величины

Определение. Случайной величиной называется величина, которая в результате опыта, принимает числовое значение, являющееся случайным событием этого опыта. Множество всех таких значений будем называть множеством возможных значений случайной величины

_{Определение. называется функцией распределения случайной величины .}

Свойства функции распределения:

1) 0<=<=1;

2) P{<=<}=-;

3) <=, если <;

4) (-)=0, (+)=1.

5) P( =) =

Определение. Рядом (или законом распределения) дискретной случайной величины называют таблицу, в первой строке которой возможные значения , а во второй - соответствующие вероятности =P{=}; =1.

Характеристиками положения случайной величины являются математическое ожидание, мода и медиана.

Определение. Средним значением, или математическим ожиданием дискретной случайной величины называют

M[]= (1)

Свойства математического ожидания:

1) M[C]=C, где С - const;

2) M[C]=CM[];

3) M[]=M[]+M[], где и - любые случайные величины;

4) M[]=M[] M[], если и - независимые случайные величины.

Случайные величины и называются независимыми, если для любых x и y имеет место равенство F(x,y) = ,т.е. P({<x, <y})=P({<x})P({<y}).

Модой () дискретной случайной величины называется ее наиболее вероятное значение.

Начальные и центральные моменты k-го порядка случайной величины определяются соответственно формулами:

=M[] и =M[].

Если дискретная случайная величина, то =, =.

Первый начальный моментявляется математическим ожиданием случайной величины

Второй центральный момент является дисперсией случайной величины :

D[]=M[]= (2)

Для вычислений удобна следующая формула:

=M[]-.

Свойства дисперсии:

1) D[C]=0, где C-const;

2) D[C]=D[];

3) если и - независимые случайные величины, то D[+]=D[]+D[].

Непрерывные случайные величины

Пусть - непрерывная случайная величина и ее функция распределения непрерывна на множестве действительных чисел.

_{Определение.} Плотностью вероятности назовем функцию ₌

Свойства плотности вероятности:

1) >=0;

2) =1;

3) =

4) P{<<}=

Непрерывная случайная величина задается либо функцией распределения , либо плотностью вероятности . Заметим, что функцию называют еще плотностью распределения случайной величины .

Определение. Средним значением, или математическим ожиданием непрерывной случайной величины называют число

M[]= , причем предполагается, что интеграл сходятся абсолютно.

Определение. Дисперсией случайной величины называется число

D[]=M[]

Для непрерывной случайной величины дисперсию можно найти по формуле

D[]=, причем предполагается, что интеграл сходятся абсолютно.

Начальные и центральные моменты k-го порядка случайной величины определяются соответственно формулами:

=M[] и =M[].

Если непрерывная случайная величина, то

= =

Первый начальный моментявляется математическим ожиданием случайной величины

Второй центральный момент является дисперсией случайной величины :

Заметим, что размерность величин и совпадает с размерностью самой случайной величины , а размерность равна квадрату размерности .

Биноминальное распределение

Определение. Биномиальное распределение — распределение количества наступлений события A в последовательности из n независимых случайных экспериментов, таких, что вероятность наступления события A в каждом из них постоянна и равна p.

Формула Бернулли является аналитическим выражением искомого закона распределения.

Таблица №1

Математическое ожидание	np
Дисперсия	npq

Задача №1.

Стрелок стреляет 9 раз по мишени. Вероятность попадания в цель при одном выстреле Написать в виде теблицы (матрицы) закон распределения случайной величины X – число попаданий по мишени. Проверить, что сумма всех вероятностей в таблице равна 1. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №1. Найти среднее квадратическое отклонение. Найти вероятность того, что стрелок попадет более 5 раз по мишени.

Решение.

Формула Бернулли:

>

Матрица распределения:

>

Проверим, что сумма всех вероятностей во второй строке равна 1.

>

Найдем математическое ожидание:

>

>

По формуле: результат подтверждается.

Найдем дисперсию:

>

>

По формуле: результат подтверждается.

Найдем среднее квадратическое отклонение:

>

>

Вероятность того, что стрелок попадет более 5 раз равна:

>

>

76, 16%.

Распределение Пуассона

Пусть производится n независимых испытаний в каждом из которых вероятность появления события A равна p. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа (см. Лабораторную работу № 3). Однако эта формула не пригодна, если вероятность события мала (npq<9). В этих случаях прибегают к асимптотической формуле Пуассона.

Данное распределение в лабораторной работе №4 не будет рассматриваться, так как возможности математического пакета Maple позволяют рассчитывать вероятность непосредственно по формуле Бернулли при ОЧЕНЬ больших n и при ОЧЕНЬ малых p , как собственно и стандартный калькулятор встроенный в программу Windows. А расчеты по прямой формуле имеют гораздо меньшую погрешность, а значит и большую ценность, чем по асимптотическим. Данный вопрос вынесен на практические занятия.

Геометрическое распределение

Пусть производятся независимые испытаний, в каждом из которых вероятность появления события A равна p (0<p<1) и, следовательно, вероятность его непоявления Испытания заканчиваются как только появляется событие A. Таким образом, если событие A появилось на k-м испытании, то в предшествующих k-1 испытаниях оно не появлялось.

Обозначим через Х дискретную случайную величину – число испытаний, которое нужно провести до первого появления события A. Возможные значения X – весь натуральный ряд. Вероятность рассчитывается по формуле:

Таблица №2

Математическое ожидание
Дисперсия

Задача №2.

Из орудия производится стрельба до первого попадания. Вероятность попадания в цель X – дискретная случайная величина числа испытаний. Составить таблицу (матрицу) распределения для X=1,2,…10. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №2. Найти среднее квадратическое отклонение. Сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени?

Решение:

Вероятность будет рассчитываться по формуле:

>

Составим первые 10 столбцов таблицы (матрицы) распределения. Очевидно, что вся таблица – бесконечна.

>

Убедимся, что сумма всех вероятностей во второй строке распределения равна 1, для этого составим ряд:

>

Найдем математическое ожидание:

>

По формуле: результат подтверждается.

Найдем дисперсию:

>

D=0.56

По формуле: результат подтверждается.

Найдем среднее квадратическое отклонение:

>

>

Ответим на вопрос сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени

>

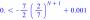
Вызовом контекстного меню, решаем данное неравенство :

>

Итак, уже при шести выстрелах, вероятность поражения хотя бы один раз мишень достигнет 0,999.

Гипергеометрическое распределение

Задача. Пусть в группе N студентов из них M отличники (M<N). Из группы случайно отбирают n студентов для прохождения тестирования (каждый студент может быть отобран с одинаковой вероятностью). Обозначим через Х случайную величину – m отличников среди n отобранных. Очевидно, возможные значения X таковы: 0,1,2…, min(M,n).

Искомая вероятность события X=m

Эта формула определяет распределение вероятностей, которое называют гипергеометрическим.

Таблица №3

Математическое ожидание
Дисперсия
Мода

Задача №3

Пусть в группе 30 студентов из них 9 отличники. Из группы случайно отбирают 4 студента для прохождения тестирования (каждый студент может быть отобран с одинаковой вероятностью). Обозначим через Х случайную величину – m отличников среди 4 отобранных. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №3. Найти среднее квадратическое отклонение. Найти наивероятнейшее число отличников, попавших на тестирование.

Решение.

Вероятность того, в отобранную группу попадут n отличников рассчитаем по формуле:

>

Таблица (матрица) распределения будет иметь вид:

>

Проверка:

>

Математическое ожидание

>

По формуле: результат подтверждается.

Найдем дисперсию:

>

>

По формуле: результат подтверждается:

>

Найдем среднее квадратическое отклонение:

>

>

Найдем наивероятнейшее число отличников, попавших на тестирование по таблице распределения – это один.

Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Таблица №4

Математическое ожидание
Дисперсия

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

-отклонение при стрельбе.

-погрешности измерений (однако погрешности некоторых измерительных приборов имеют не нормальные распределения).

-некоторые характеристики живых организмов в популяции.

-исследование свойств личности человека в психологии и психиатрии.

Задача №4

Конфеты, изготовляемые на конвейере фабрики, считаются годными, если отклонение диаметра конфеты от проектного размера не превышает 2мм. Случайные отклонения диаметра конфет подчиняется нормальному закону со средним квадратическим отклонением мм и математическим ожиданием m=0. Сколько годных конфет изготовляет фабрика? Дать графическую интерпретации решению задачи.

Решение.

>

>

Фабрика изготовляет 78,87% годных конфет.

>

Равномерное распределение

Распределение вероятностей называют равномерным, если на интервале которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Плотность вероятности равномерного распределения

Таблица №5

Математическое ожидание
Дисперсия

Показательное распределение

Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается:

где λ>0.

Таблица №6

Математическое ожидание
Дисперсия

Контрольные задания

• Оформите титульный лист к лабораторной работе, согласно требованиям СФМЭИ (ТУ). Укажите название лабораторной работы. Фамилию, Имя, группу, номер студента в журнале (см. Приложение 1).

• Создайте документ Maple. Напишите заголовок 14 кеглем, полужирно, с выравниванием по центру: «Лабораторная работа №_». Далее с выравниванием по правому краю, курсивом, 14 кеглем укажите полностью Фамилию, Имя, номер в журнале.

• Выполните задания из своего варианта, определяемого номером в журнале. Каждое задание должно быть оформлено в отдельной секции (пиктограммы ) с заголовком «Задание №_». Завершать секцию должен развернутый ответ.

• Распечатайте лабораторную работу из под программы Maple на листах формата А4 (односторонняя печать).

При выполнении контрольных заданий студенту необходимо подставить вместо буквенных параметров индивидуальные анкетные характеристики:

- число букв в фамилии студента,

- число букв в полном имени студента,

- номер студента по списку в журнале.

В отчете на титульном листе необходимо обязательно указать, какие анкетные данные использовались при выполнении контрольных заданий (имя, фамилия, номер варианта).

Задания.

Задача №1.

Стрелок стреляет 9 раз по мишени. Вероятность попадания в цель при одном выстреле Написать в виде таблицы (матрицы) закон распределения случайной величины X – число попаданий по мишени. Проверить, что сумма всех вероятностей в таблице равна 1. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №1. Найти среднее квадратическое отклонение. Найти вероятность того, что стрелок попадет не менее 5 раз по мишени. Указать наивероятнейшее число попаданий.

Задача №2.

Из орудия производится стрельба до первого попадания. Вероятность попадания в цель X – дискретная случайная величина числа испытаний. Составить таблицу (матрицу) распределения для X=1,2,…10. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №2. Найти среднее квадратическое отклонение. Сколько раз надо сделать выстрелов, чтобы с вероятностью 0,999 попасть по мишени?

Задача №3.

Пусть в группе 40 студентов из них a+b отличники. Из группы случайно отбирают с+a студентов для прохождения тестирования (каждый студент может быть отобран с одинаковой вероятностью). Обозначим через Х случайную величину – m отличников среди отобранных. Найти по формулам (1) и (2) математическое ожидание и дисперсию. Подтвердить полученные результаты по формулам из таблицы №3. Найти среднее квадратическое отклонение. Найти наивероятнейшее число отличников, попавших на тестирование.

Задача №4

Валики, изготовляемые на конвейере фабрики, считаются годными, если отклонение диаметра валика от проектного размера не превышает a (мм). Случайные отклонения диаметра валиков подчиняется нормальному закону со средним квадратическим отклонением мм и математическим ожиданием m=0. Сколько годных валиков изготовляет фабрика? Дать графическую интерпретации решению задачи.

Задача №5

Цена деления шкалы амперметра равна 0,1 A. Показания округляют до ближайшего целого деления. Найти вероятность того, при отсчете будет сделана ошибка превышающая А.

Задача №6

Плотность случайной величины ξ задана законом

Вычислить значение параметра A. Построить функцию распределения случайной величины . Определить случайную величину. Найти вероятности попадания случайной величины в интервал (0, ), (). 4) Найти числовые характеристики по определению, проверить результаты по таблице №6.