Правило исключения интервалов

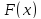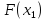Если известно, что критерий оптимизации - унимодальная функция, то при помощи любой пары наблюденийи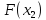можно значительно сузить зону поиска и указать интервал, в котором находится экстремум. Определить интервал, содержащий экстремум, на основании двух измерений функции позволяет правило исключения интервалов.

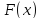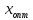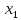Пусть на замкнутом интервале функцияунимодальна, а её минимум достигается в точке. Рассмотрим точкии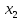, расположенные на интервале таким образом, что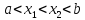. Сравнивая значения функции в точкахи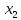, можно сделать следующие выводы:

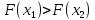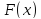• если , то точка минимумане лежит в интервал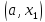е, т.е.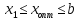

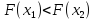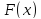• если , то точка минимумане лежит в интервал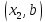е, т.е.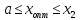

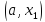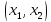• если , то можно исключить оба крайних интервалаи. При этом точка минимума должна располагаться в интервале, т.е.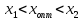

Правило исключения интервалов устраняет необходимость полного перебора всех допустимых точек. Методы поиска, которые позволяют определить оптимум функции одной переменной путём последовательного исключения подинтервалов и, следовательно, путём сокращения интервала поиска, носят название методов исключения интервалов.

В процессе применения методов исключения интервалов можно выделить два этапа:

• Установление границ интервала, содержащего экстремум. В поисковых задачах оптимизации отрезок, на котором располагается точка минимума, называют интервалом неопределённости.

• Уменьшение интервала, на котором реализуется конечная последовательность преобразований исходного интервала с тем, чтобы уменьшить его длину до заранее установленной величины 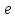, определяющей точность поиска экстремума.

Унимодальность

В общем виде задача оптимизации формулируется следующим образом: минимизировать функцию 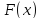, для всех, принадлежащих допустимой области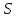. Если ограничения отсутствуют, то область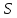расширяется до открытого действительного пространства, и задача называется задачей безусловной оптимизации. Учёт дополнительной информации о функции может сделать поиск экстремума (обычно будем подразумевать поиск минимума) более эффективным. Например, о функции может быть известно, что она имеет только один экстремум, или что она монотонна, или что её вторая производная всюду сохраняет знак и т.п.

Среди возможных дополнительных сведений о функции 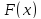наиболее ценным и наименее обременительным является её свойство унимодальности (одноэкстремальности).

Определение: функция 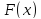является унимодальной на отрезке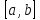в том и только в том случае, если она монотонна по обе стороны от единственной на рассматриваемом интервале оптимальной точки.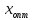

Иначе говоря, если 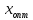- единственная точка минимума функциина отрезке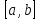, то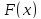оказывается унимодальной на этом интервале тогда и только тогда, когда для точек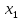и: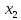

• из 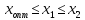следует, что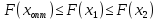

• из следует, что

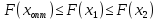
Надо отметить, что унимодальная функция не обязательно должна быть непрерывной. Унимодальность функций является исключительно важным свойством, которое широко используется в оптимизационных исследованиях.

ШАГИ АЛГОРИТМА ПАУЭЛЛА

~~~~~~~~~~~~~~~~~~~~~~

ШАГ 1: ВЫЧИСЛИТЬ X2 = x1 + d, F2 = F(X2), F1 = F(X1)

ШАГ 2: ЕСЛИ F1 > F2, ПОЛОЖИТЬ X3 = X2 + d

ЕСЛИ F1 <=F2, ПОЛОЖИТЬ X3 = X1 - d. ВЫЧИСЛИТЬ F3 = F(X3)

ШАГ 3: НАЙТИ Fmin = min [F1,F2,F3] И СООТВЕТСТВУЮЩЕЕ Xmin

ШАГ 4: ПО ТОЧКАМ 1,2,3 ВЫЧИСЛИТЬ ЭКСТРЕМУМ АППРОКСИМ.ПОЛИНОМА ПО

ФОРМУЛАМ (2),(3),(4)

ШАГ 5: ПРОВЕРИТЬ, ВЫПОЛНЯЕТСЯ ЛИ УСЛОВИЕ:

- -

|Fmin - F | <= E1 |Xmin - X | <= E2

ГДЕ E1 И E2 - ТОЧНОСТЬ РЕШЕНИЯ ПО ФУНКЦИИ И АРГУМЕНТУ.

ЕСЛИ УСЛОВИЯ ВЫПОЛНЕНЫ -ЗАКОНЧИТЬ ПОИСК.ЗА X* ПРИНЯТЬ ЛУЧШУЮ

-

ИЗ Xmin И X .ЕСЛИ НЕТ - ПЕРЕЙТИ К ШАГУ 6. -

ШАГ 6: ВЫБРАТЬ "ХУДШУЮ" ИЗ ТРЕХ ТОЧЕК, ПРИСВОИТЬ ЕЙ ЗНАЧЕНИЕ X ,

ОСТАВИВ ПРЕЖНИЙ ИНДЕКС.ПЕРЕЙТИ К ШАГУ 4.

7. МЕТОД ЗОЛОТОГО СЕЧЕНИЯ

~~~~~~~~~~~~~~~~~~~~~~~~~~

МЕТОД ЗОЛОТОГО СЕЧЕНИЯ СОСТОИТ В ПОСТРОЕНИИ ПОСЛЕДОВАТЕЛЬНОСТИ

ОТРЕЗКОВ [a0,b0], [a1,b1], ..., СТЯГИВАЮЩИХСЯ К ТОЧКЕ МИНИМУМА ФУН-

КЦИИ F(X). НА КАЖДОМ ШАГЕ, ЗА ИСКЛЮЧЕНИЕМ ПЕРВОГО, ВЫЧИСЛЕНИЕ ЗНАЧЕ-

НИЯ ФУНКЦИИ ПРОИЗВОДИТСЯ ЛИШЬ В ОДНОЙ ТОЧКЕ. ЭТА ТОЧКА, НАЗЫВАЕМАЯ

"ЗОЛОТЫМ СЕЧЕНИЕМ", ВЫБИРАЕТСЯ СЛЕДУЮЩИМ ОБРАЗОМ.

ПУСТЬ ДЛИНА ИСХОДНОГО ИНТЕРВАЛА НЕОПРЕДЕЛЕННОСТИ РАВНА L,

А ТОЧКА ДЕЛИТ ЕГО НА ДВЕ ЧАСТИ: L1 И L2 , ПРИЧЕМ L1 > L2 И

L1 + L2 = L.

"ЗОЛОТОЕ СЕЧЕНИЕ" ИНТЕРВАЛА НЕОПРЕДЕЛЕННОСТИ ВЫБИРАЕТСЯ

ТАК, ЧТОБЫ ОТНОШЕНИЕ ДЛИНЫ БОЛЬШЕГО ОТРЕЗКА К ДЛИНЕ ВСЕГО ИН-

ТЕРВАЛА РАВНЯЛОСЬ ОТНОШЕНИЮ ДЛИНЫ МЕНЬШЕГО ОТРЕЗКА К ДЛИНЕ БОЛЬ-

ШЕГО ОТРЕЗКА: L1/L = L2/L1 ...(*).

ИЗ ЭТОГО СООТНОШЕНИЯ НАЙДЕМ ТОЧКУ ДЕЛЕНИЯ.

ОБОЗНАЧИМ ОТНОШЕНИЕ L2/L1 ЧЕРЕЗ T. ПОДСТАВИМ ЕГО

В УРАВНЕНИЕ (*). ПОЛУЧИМ:

L1/(L1 + T*L1) = T

СОКРАТИВ ДРОБЬ НА L1 , ПОЛУЧИМ: T*T + T - 1 = 0

РЕШЕНИЕ ЭТОГО УРАВНЕНИЯ ДАЕТ :

T = 0.5 *(-1 + SQR(5)) = 0.61804...

ТАКИМ ОБРАЗОМ, ПРИ ЗОЛОТОМ СЕЧЕНИИ ДЛИНА БОЛЬШЕГО

ОТРЕЗКА L1 ОКАЗАЛАСЬ РАВНОЙ L*T, А ДЛИНА МЕНЬШЕГО

ОТРЕЗКА : L*(1-T), ГДЕ (1 - T) = 0.38196...

ПОСКОЛЬКУ ЗАРАНЕЕ НЕИЗВЕСТНО, В КАКОЙ ПОСЛЕДОВА-

ТЕЛЬНОСТИ: L1 И L2 ИЛИ L2 И L1 НАДО ДЕЛИТЬ ИНТЕРВАЛ,

РАССМАТРИВАЮТ ТОЧКИ, СООТВЕТСТВУЮЩИЕ ДВУМ СПОСОБАМ ДЕ-

ЛЕНИЯ.

НА СЛЕДУЮЩЕМ КАДРЕ ВАМ БУДЕТ ПРЕДЛОЖЕН АЛГОРИТМ

МЕТОДА. ОН СОСТОИТ ИЗ РЯДА ШАГОВ. ЗАПИШИТЕ ШАГИ АЛГОРИТМА.

~~~~~~~~~~~~~~~~~~~~~~

ГЕОМЕТРИЧЕСКАЯ ИЛЛЮСТРАЦИЯ МЕТОДА "ЗОЛОТОГО СЕЧЕНИЯ"

. .

| . . |

| * . |

| |. .* |

| | . . | |

| | . .* | |

| | * | | |

| | | | | |

$---------|-----$--|-----$-------------$ 1-ая итерация

a1 | | x1 | | x2| b1

| | | | |

a2 $---------$-----$--|-----$ 2-ая итерация

x1| x2| | b2|

| | | |

$-----$--$-----$ 3-ья итерация

a2 x1 x2 b3

КАК ВИДИМ, ТОЛЬКО НА ПЕРВОЙ ИТЕРАЦИИ ВЫЧИСЛЯЮТСЯ ДВЕ

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ПРОМЕЖУТОЧНЫЕ ТОЧКИ. НА ВСЕХ ОСТАЛЬНЫХ - ОДНА, ПОСКОЛЬКУ

~~~~~~~~~~~~~~~~~~~

ДРУГАЯ ПЕРЕНОСИТСЯ С ПРЕДЫДУЩЕЙ ИТЕРАЦИИ.

ОДНАКО СЛЕДУЕТ ИМЕТЬ В ВИДУ, ЧТО ДЛЯ БОЛЬШЕЙ ТОЧНОСТИ

********************

НА КАЖДОЙ ИТЕРАЦИИ ЛУЧШЕ ОПРЕДЕЛЯТЬ ДВЕ НОВЫЕ ТОЧКИ, А НЕ ОДНУ,

***************************************************************

ПОСКОЛЬКУ ЗНАЧЕНИЕ T1 НЕ ЯВЛЯЕТСЯ ТОЧНЫМ. ПРИ ОПЕРИРОВАНИИ

ТОЛЬКО С ОДНОЙ НОВОЙ ТОЧКОЙ ОШИБКИ ОКРУГЛЕНИЯ ПРИ ВЫЧИСЛЕНИИ МО-

ГУТ ПРИВЕСТИ К ПОТЕРЕ ИНТЕРВАЛА, СОДЕРЖАЩЕГО МИМИНУМ.

АЛГОРИТМ МЕТОДА "ЗОЛОТОГО СЕЧЕНИЯ"

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

ШАГ 1: ВЫЧИСЛИТЬ L=b-a

ШАГ 2: ПОЛОЖИТЬ x1=a + L*T1, x2=b-L*T1, ГДЕ T1=0.38196

ВЫЧИСЛИТЬ ЗНАЧЕНИЯ F(x1) И F(x2).

ШАГ 3: СРАВНИТЬ ЗНАЧЕНИЯ ФУНКЦИИ В ДВУХ ТОЧКАХ.

(1) ЕСЛИ F(x1)<F(x2), ТО ИСКЛЮЧАЕТСЯ ИНТЕРВАЛ (x2,b].

ПОЛАГАЕМ b=x2, x2=x1. ПЕРЕХОДИМ К ШАГУ 4.

(2) ЕСЛИ F(x1)>=F(x2), ТО ИСКЛЮЧАЕТСЯ ИНТЕРВАЛ [a,X1).

ПОЛАГАЕМ a=x1, x1=x2.

ШАГ 4: ВЫЧИСЛИТЬ L=b-a. ЕСЛИ ВЕЛИЧИНА L МАЛА, ЗАКОНЧИТЬ ПОИСК.

В ПРОТИВНОМ СЛУЧАЕ ВЕРНУТЬСЯ К ШАГУ 2 НА РАСЧЕТ НЕДОСТА-

ЮЩЕЙ ТОЧКИ.

В КАЧЕСТВЕ ОПТИМАЛЬНОГО ЗНАЧЕНИЯ X МОЖНО ПРИНЯТЬ X=a (ЛИБО X=b,

ЛИБО X=0.5(a+b) ).

ПРОЦЕДУРА АППРОКСИМАЦИИ СОСТАВЛЯЕТ ОСНОВУ

МЕТОДА ПАУЭЛЛА ОДНОМЕРНОЙ ОПТИМИЗАЦИИ.

НА СЛЕДУЮЩИХ КАДРАХ ПРЕДСТАВЛЕНЫ ШАГИ АЛГОРИТМА

ПАУЭЛЛА. ЗАПИШИТЕ ИХ В ТЕТРАДЬ. ОНИ ВАМ ПОНАДОБЯТСЯ

~~~~~~~~~~~~~~~~~~~~~

ПРИ РЕШЕНИИ ЗАДАЧ.

В АЛГОРИТМА ПАУЭЛЛА В КАЧЕСТВЕ ИСХОДНЫХ ДАННЫХ БЕРУТСЯ:

~~~~~~~~~~~~~~~~~

ИСХОДНАЯ ТОЧКА X1 И ВЕЛИЧИНА ПЕРЕМЕЩЕНИЯ d.

ШАГ 1: ВЫЧИСЛИТЬ X2 = X1 + d

~~~~~ ВЫЧИСЛИТЬ F1 = F(X1) И F2 = F(X2)

ШАГ 2: ЕСЛИ F1 > F2 , Т.Е. НАПРАВЛЕНИЕ ИЗМЕНЕНИЯ X УДАЧНОЕ,

~~~~~~ ПОЛОЖИТЬ X3 = X2 + d. ЕСЛИ F1 <= F2, T.E. НАПРАВЛЕНИЕ

НЕУДАЧНОЕ, ПОЛОЖИТЬ X3 = X1 - d. ВЫЧИСЛИТЬ F3 = F(X3).

ШАГ 3: НАЙТИ Fmin = min[F1,F2,F3] И СООТВЕТСТВУЮЩЕЕ ЗНАЧЕНИЕ

~~~~~~ Xmin.

-

ШАГ 4: ПО ТОЧКАМ X1,X2,И X3 ВЫЧИСЛИТЬ X ,ИСПОЛЬЗУЯ ФОРМУЛЫ

~~~~~ (2),(3),(4).ВЫЧИСЛИТЬ СООТВЕТСТВУЮЩЕЕ ЗНАЧЕНИЕ

- -

F = F(X).

ШАГ 5: ПРОВЕРКА НА ОКОНЧАНИЕ ПОИСКА: -

***** а) ЯВЛЯЕТСЯ ЛИ РАЗНОСТЬ |Fmin - F | <= E1 ?

-

б) ЯВЛЯЕТСЯ ЛИ РАЗНОСТЬ |Xmin - X | <= E2 ?

ЕСЛИ ОБА УСЛОВИЯ ВЫПОЛНЯЮТСЯ - ЗАКОНЧИТЬ ПОИСК. -

ЗА ОПТИМАЛЬНУЮ ПРИНЯТЬ ТОЧКУ, ЛУЧШУЮ ИЗ Xmin И X .

В ПРОТИВНОМ СЛУЧАЕ ПЕРЕЙТИ К ШАГУ 6.

ШАГ 6: ВЫБРАТЬ "ХУДШУЮ" (С ТОЧКИ ЗРЕНИЯ ЗНАЧЕНИЯ ФУНКЦИИ)

***** ИЗ ТРЕХ ТОЧЕК: X1,X2,X3 - И ПРИСВОИТЬ ЕЙ ЗНАЧЕНИЕ

-

X , ОСТАВИВ ПРЕЖНИЙ ИНДЕКС.

СРАВНЕНИЕ ЭФФЕКТИВНОСТИ РАССМОТРЕННЫХ МЕТОДОВ

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~

ЭФФЕКТИВНОСТЬ МЕТОДОВ ИСКЛЮЧЕНИЯ ИНТЕРВАЛОВ МОЖНО ОЦЕНИТЬ

ОТНОШЕНИЕМ ИНТЕРВАЛА НЕОПРЕДЕЛЕННОСТИ ПОСЛЕ N ВЫЧИСЛЕНИЙ

ЦЕЛЕВОЙ ФУНКЦИИ К НАЧАЛЬНОМУ ИНТЕРВАЛУ НЕОПРЕДЕЛЕННОСТИ.

ТАКАЯ ФУНКЦИЯ ЭФФЕКТИВНОСТИ ПРЕДЛОЖЕНА Д.ДЖ.УАЙЛДОМ.

ОБОЗНАЧИМ ЕЕ ЧЕРЕЗ E.

НА СЛЕДУЮЩЕМ КАДРЕ ПРЕДСТАВЛЕНА ТАБЛИЦА, СОДЕРЖАЩАЯ ЗНА-

ЧЕНИЯ Е ,СООТВЕТСТВУЮЩИЕ РАЗЛИЧНЫМ КОЛИЧЕСТВАМ ВЫЧИСЛЕНИЙ

ЦЕЛЕВОЙ ФУНКЦИИ N ДЛЯ ТРЕХ МЕТОДОВ ПОИСКА.

ЗАПИШИТЕ ЕЕ И ПОСТАРАЙТЕСЬ ЗАПОМНИТЬ ДЛЯ N = 10.

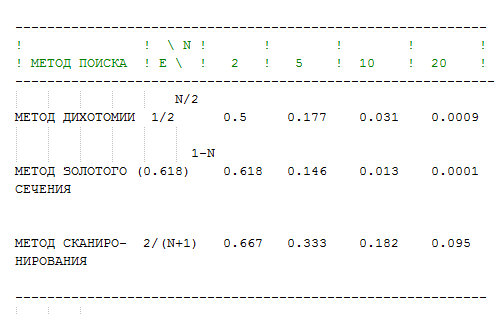
ИЗ ТАБЛИЦЫ СЛЕДУЕТ, ЧТО НАИБОЛЕЕ ЭФФЕКТИВНЫМ

ЯВЛЯЕТСЯ МЕТОД ЗОЛОТОГО СЕЧЕНИЯ.

ОН ЭФФЕКТИВНЕЕ МЕТОДА СКАНИРОВАНИЯ

В 950 !!! РАЗ ( ПРИ N = 20 )

ПРОВЕДЕМ ТАКЖЕ СРАВНЕНИЕ МЕТОДОВ ПО КОЛИЧЕСТВУ

-------------

ВЫЧИСЛЕНИЙ ЗНАЧЕНИЙ ФУНКЦИИ, ТРЕБУЕМОМУ ДЛЯ ДОСТИЖЕНИЯ

---------------------------

ЗАДАННОЙ ВЕЛИЧИНЫ ОТНОСИТЕЛЬНОГО УМЕНЬШЕНИЯ ИНТЕРВАЛА

НЕОПРЕДЕЛЕННОСТИ, ИЛИ ЗАДАННОЙ СТЕПЕНИ ТОЧНОСТИ.

ЕСЛИ ВЕЛИЧИНА E ЗАДАНА, ТО ЗНАЧЕНИЕ N ВЫЧИСЛЯЕТСЯ

ПО СЛЕДУЮЩИМ ФОРМУЛАМ.

МЕТОД ДИХОТОМИИ :

N = 2 Ln ( E ) / Ln 0.5

МЕТОД ЗОЛОТОГО СЕЧЕНИЯ:

N = 1 + ( Ln ( E ) / Ln ( 0.618 ))

МЕТОД СКАНИРОВАНИЯ:

N = ( 2 / E ) - 1

В ТАБЛИЦЕ ПРИВЕДЕНЫ КОЛИЧЕСТВА ВЫЧИСЛЕНИЙ F(X) НЕОБХОДИ-

МЫХ ДЛЯ ОПРЕДЕЛЕНИЯ КООРДИНАТЫ ТОЧКИ МИНИМУМА С ЗАДАННОЙ ТОЧНОСТЬЮ:

ПЕРЕХОДИТЕ К ИЗУЧЕНИЮ СЛЕДУЮЩЕГО РАЗДЕЛА КУРСА (КЛАВИША "ДАЛЬШЕ").

ЕСЛИ ХОТИТЕ ВЫЙТИ НА ПЕРЕЧЕНЬ РАЗДЕЛОВ КУРСА - ВВЕДИЕ 1.

НА ЭТОМ ВЫ ЗАКАНЧИВАЕТЕ ИЗУЧЕНИЕ МЕТОДОВ

ОДНОМЕРНОЙ МИНИМИЗАЦИИ

ВЫ ПОЗНАКОМИЛИСЬ С НАЗНАЧЕНИЕМ, ОБЛАСТЬЮ

ПРИМЕНЕНИЯ МЕТОДОВ, ИЗУЧИЛИ ОСНОВНЫЕ АЛГОРИТМЫ

МЕТОДОВ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ.

МЕТОДЫ ТОЧЕЧНОГО ОЦЕНИВАНИЯ. МЕТОД ПАУЭЛЛА.

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

СЕЙЧАС МЫ ПОЗНАКОМИМСЯ С ГРУППОЙ ЧИСЛЕННЫХ МЕТОДОВ

ОДНОМЕРНОЙ ОПТИМИЗАЦИИ,ТРЕБУЮЩИХ ОТ ФУНКЦИИ, КРОМЕ У Н И -

М О Д А Л Ь Н О С Т И , ЕЩЕ И Н Е П Р Е Р Ы В Н О С Т Ь .

ВВЕДЕНИЕ ДОПОЛНИТЕЛЬНОГО ТРЕБОВАНИЯ ДЕЛАЕТ МЕТОДЫ

*************************************************

ЭТОЙ ГРУППЫ БОЛЕЕ ЭФФЕКТИВНЫМИ, ЧЕМ МЕТОДЫ ИСКЛЮЧЕНИЯ ИН-

******************************

ТЕРВАЛОВ.

ОСНОВНАЯ ИДЕЯ РАССМАТРИВАЕМОГО МЕТОДА СВЯЗАНА С ВОЗ-

************* ******

МОЖНОСТЬЮ АППРОКСИМАЦИИ ГЛАДКОЙ ФУНКЦИИ ПОЛИНОМОМ И ПОС-

*************

ЛЕДУЮЩЕГО ИСПОЛЬЗОВАНИЯ АППРОКСИМИРУЮЩЕГО ПОЛИНОМА ДЛЯ

ОЦЕНИВАНИЯ КООРДИНАТЫ ТОЧКИ ОПТИМУМА.

СОГЛАСНО ТЕОРЕМЕ ВЕЙЕРШТРАССА ОБ АППРОКСИМАЦИИ, ЕСЛИ

ФУНКЦИЯ НЕПРЕРЫВНА В НЕКОТОРОМ ИНТЕРВАЛЕ, ТО ЕЕ МОЖНО С

ЛЮБОЙ СТЕПЕНЬЮ ТОЧНОСТИ АППРОКСИМИРОВАТЬ ПОЛИНОМОМ ДОСТА-

ТОЧНО ВЫСОКОГО ПОРЯДКА.

КАЧЕСТВО ОЦЕНОК КООРДИНАТЫ ТОЧКИ ОПТИМУМА, ПОЛУЧА-

ЧАЕМЫХ С ПОМОЩЬЮ АППРОКСИМИРУЮЩЕГО ПОЛИНОМА, МОЖНО ПОВЫСИТЬ:

1) ИСПОЛЬЗОВАНИЕМ ПОЛИНОМА БОЛЕЕ ВЫСОКОГО ПОРЯДКА;

2) УМЕНЬШЕНИЕМ ИНТЕРВАЛА.

ВТОРОЙ СПОСОБ ЯВЛЯЕТСЯ БОЛЕЕ ПРЕДПОЧТИТЕЛЬНЫМ, ПО-

СКОЛЬКУ ПОСТРОЕНИЕ АППРОКСИМИРУЮЩЕГО ПОЛИНОМА ПОРЯДКА ВЫШЕ

3-ЕГО СТАНОВИТСЯ ВЕСЬМА СЛОЖНОЙ ПРОЦЕДУРОЙ, ТОГДА КАК УМЕНЬ-

ШЕНИЕ ИНТЕРВАЛА В УСЛОВИЯХ, КОГДА ВЫПОЛНЯЕТСЯ ПРЕДПОЛОЖЕНИЕ

ОБ УНИМОДАЛЬНОСТИ ФУНКЦИИ, ОСОБОЙ СЛОЖНОСТИ НЕ ПРЕДСТАВЛЯЕТ.

ОДИН ИЗ МЕТОДОВ ЭТОЙ ГРУППЫ- МЕТОД ПАУЭЛЛА,

*************

ОСНОВАН НА ПОСЛЕДОВАТЕЛЬНОМ ИЗМЕНЕНИИ ПРОЦЕДУРЫ ОЦЕНИ-

ВАНИЯ С ИСПОЛЬЗОВАНИЕМ КВАДРАТИЧНОЙ АППРОКСИМАЦИИ.

***************************

ЕСЛИ ЗАДАНА ПОСЛЕДОВАТЕЛЬНОСТЬ ТОЧЕК: X1, X2, X3

И ИЗВЕСТНЫ СООТВЕТСТВУЮЩИЕ ЭТИМ ТОЧКАМ ЗНАЧЕНИЯ ФУНКЦИИ

F1, F2, F3, ТО МОЖНО ОПРЕДИЛИТЬ ПОСТОЯННЫЕ ВЕЛИЧИНЫ

a0, a1, a2 ТАКИМ ОБРАЗОМ, ЧТО ЗНАЧЕНИЕ КВАДРАТИЧНОГО

ПОЛИНОМА: G(x)=a0+a1*(x-x1)+a2*(x-x1)*(x-x2) СОВПА-

ДАЮТ СО ЗНАЧЕНИЕМ F(x) В 3-Х УКАЗАНЫХ ТОЧКАХ.

РАССЧИТАЕМ КОЭФФИЦИЕНТЫ ПОЛИНОМА F(X).

ФОРМУЛЫ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТОВ ЗАПИШИТЕ В ТЕТРАДЬ!

F1=F(X1)=a0+a1*(X1-X1)+a2*(X1-X1)*(X1-X2)=a0

ОТСЮДА: a0=F1 ...... (1)

F2=F(X2)=a0+a1*(X2-X1)+(X2-X1)*(X2-X2)*a2 =

=a0+a1*(X2-X1)

ОТСЮДА: a1=(F2-F1)/(X2-X1) .... (2)

F3=F(X3)=a0+a1*(X3-X1)+a2*(X3-X1)*(X3-X2)=

=F1+(F2-F1)*(X3-X1)/(X2-X1)+a2*(X3-X1)*(X3-X2)

ОТСЮДА: a2=((F3-F1)/(X3-X1)-a1)/(X3-X2)... (3)

ЗНАЯ КОЭФФИЦИЕНТЫ a0, a1, a2 АПРОКСИМИРУЮЩЕГО ПОЛИ-

-

НОМА F(X), МОЖНО ВЫЧИСЛИТЬ КООРДИНАТУ ТОЧКИ ЭКСТРЕМУМА X

ПУТЕМ ПРИРАВНИВАНИЯ НУЛЮ 1-ОЙ ПРОИЗВОДНОЙ И ПОСЛЕДУЮЩЕГО

НАХОЖДЕНИЯ КОРНЕЙ ПОЛУЧЕННОГО ТАКИМ ОБРАЗОМ УРАВНЕНИЯ:

dF/dX=a1+a2*(X-X2)+a2*(X-x1)=0 (ФОРМУЛЫ ЗАПИШИТЕ!)

-

X=(a2*(X1+X2)-a1)/(2*a2)=(X1+X2)/2-a1/(2*a2)... (4)

ПОСКОЛЬКУ ФУНКЦИЯ F(X) НА РАССМАТРИВАЕМОМ ИНТЕРВАЛЕ

И АППРОКСИМИРУЮЩИЙ КВАДРАТИЧНЫЙ ПОЛИНОМ УНИМОДАЛЬНЫ , ТО

ТО МОЖНО ОЖИДАТЬ , ЧТО ЭКСТРЕМУМ ПОЛИНОМА ОКАЖЕТСЯ ВПОЛНЕ

ПРИЕМЛЕМОЙ ОЦЕНКОЙ ТОЧКИ ИСТИННОГО ЭКСТРЕМУМА ФУНКЦИИ .