По формуле (2.12.6) q ( y) =	y4	, q	( y) =	y5
					и т..дПо методу
4	4!	5		5!

математической индукции предполагаем, что qk-1 ( y) =

yk -1

, откуда

(k -1)!

y

( y - u)k -1

yk

q ( y) =

ò0

du =

.

k

(k -1)!

k !

В итоге получаем, что

1

1

1

¥

¥

M (Z ) =1 +

å

P(Z ³ k=) 1 +

= q (1)

1 +1 +

+

+

+ . .=. e.

å k

2! 3!

4!

k=2

k =1

Ответ. e » 2,7.

Задача 2.78. Пусть X1, X 2 ,¼, X n –– последовательность независимых случайных величин, каждая из которых имеет равномерное распределение в интервале (0,a).

Пусть в нечетных вариантахZ = min{n : X1 + X 2 +K+ X n ³ 2a}. В четных вариантах Z = min{n : X1 + X 2 +K+ X n ³ 3a}.

Найдите M (Z ). (См. пример 2.78, a –– номер варианта.)

2.13. Центральная предельная теорема

Формулировка центральной предельной теоремы(для одинаково распределенных слагаемых).

Пусть X1, X 2 ,¼, X n –– последовательность независимых одинаково распределенных случайных величин. Если дисперсии случайных величин конечны и отличны от ,нулято при достаточно большихn закон распределения суммы

X1 + X 2 +¼+ X n

сколь угодно близок к нормальному закону распределения.

В условиях теоремы имеет место предельное соотношение

æ	n			ö
ç	åХ i - nm			÷			1		x	e-t2 /2dx
P ç	i=1			< x ÷ ¾¾¾®
ç	s n			÷	n®¥		2p -ò¥
ç				÷
è				ø

где m = M ( Х i ), D( Хi ) = s2 .

Пример 2.79. Стрелок в десятку попадает с вероятностью0,4, в девятку –– с вероятностью 0,3, в восьмерку –– с вероятностью 0,2, в

133

семерку –– с	вероятностью 0,1.				Какова		вероятность того, что			при 25
выстрелах стрелок наберет от 220 до 240 очков?
Решение.	Пусть		при i-м		выстреле стрелок выбиваетXi					очков.
Величины Xi независимы и имеют одно и то же распределение
		X		7	8		9	10
		P		0,1	0,2		0,3	0,4

Заметим,

что M ( X i ) = 7 ×0,1 + 8 ×0, 2 + 9 ×0,3 +10 ×0,4 = 9,

а

D( X i ) =

= (7 - 9)2 ×0,1 + (8 - 9)2 ×0, 2 + (9 - 9)2 ×0,3 + (10 - 9)2 ×0, 4= 1.

25

Сумма очков Y = åX i

, будучи суммой большого числа независимых

i=1

одинаково распределенных

слагаемых

с

ограниченными

дисперсиями,

имеет закон распределения близкий к нормальному с параметрами

M (Y ) = M=(

25

)

25

М (X

)

25 ×9 = 225

=X

å

å

i

i

и

i=1

i=1

25

25

D(Y ) = D=(

)

D( X

)

25 ×1 = 25.

= X

i

å

i

å

i=1

i=1

В итоге Y ~ N (225;25). Поэтому по формуле (2.9.2)

P(220 < Y < 240)

æ 240 - 225

ö

æ 220 - 225 ö

F

ç

=

÷ - Fç

÷ =

5

è

5

ø

è

ø

= F(3) + F(1)=

0, 4986 + 0,3413=

0,8399 » 0,84.

Ответ. 0,8399 » 0,84.

Задача 2.79. Игральный

кубик

подбрасываютn

раз.

Оценить

вероятность того, что суммарное

число

очков

превзойдет3n +10.

(См.

пример 2.79, n –– номер варианта плюс 50.)

Пример 2.80. Регулировка прибора занимает время от4 до 10 мин.

Регулировщику

предстоит

отрегулировать50

приборов.

Считая

для

каждого прибора равновозможными все значения времени регулировки в

указанных	пределах,	оценить		вероятность		того, что		регулировщик
справится с работой за шесть часов.
Решение. Пусть		Xi	––	время	регулировки i-го			прибора, а
Y = X1 + X 2 + X 3 +¼+ X 50			––	время	выполнения		работы		рабочим.
Требуется найти Р(Y < 360).			Величина Y является суммой большого числа

одинаково распределенных независимых случайных величин, каждая из которых ограничена. По центральной предельной теоремеY имеет закон распределения близкий к нормальному закону распределения. Найдем

134

параметры этого закона, т.е. математическое ожидание и дисперсию величины Y. Так как случайные величины Xi независимы, то

М (Y ) = М ( X1 ) + M ( X 2 ) +¼+ М ( X 50 )

и

D(Y ) = D( X1 ) + D( X 2 ) +¼+ D( X 50 ).

Вычислим М ( X i ) и D( Xi ). По условию все значения случайной величины Xi равновозможны в отрезке [4,10]. Поэтому функция плотности вероятности этой случайной величины в указанном отрезке постоянна.

Чтобы площадь,

заключенная

между

графиком

функции

плотности

вероятности

и

осью

абсцисс, равнялась

единице,

следует

положить

f (x) =1 / 6

при х Î[4,10]

и

f (x) = 0

при

остальныхх.

С учетом этого

имеем

10

10

М ( X i ) = ò х ×1 / 6dx = 7, D(=X i ) ò(х - 7)2 ×1 / 6dx = 3.

4

4

Поэтому М (Y ) = 50 ×7 = 350,

D(Y ) = 50 ×3 =150, s(Y ) »12, 25.

Итак,

Y ~ N (350;150).

Для

вычисления

искомой

вероятности

воспользуемся формулой (2.9.2)

и

таблицей

функции

Лапласа(см. прил.,

табл. П2):

P(Y <

360)

Р(200=< Y < 360)

æ

360 - 350 ö

æ 200 - 350 ö

Fç

=

÷ - F

ç

÷

=

12, 25

è

12, 25

ø

è

ø

= F(0,82) + F(12,24)=

0,294 + 0,5 » 0,8.

Ответ. 0,794 » 0,8.

Задача 2.80.1. Регулировка каждого механизма занимает время отa до b минут. Считая все значения времени регулировки в этом интервале равновозможными, оценить вероятность того, что для регулировкиn

механизмов			рабочему			хватитm часов.				(См. пример				2.80		и	исходные
данные.)
	Исходные данные к задаче 2.80.1.
№	a	b		n	m	№	a	b		n	m	№	a			b	n	m
1	2	8		60	5	11	2	6		100	7	21		3		9	60	5
2	2	10		50	6	12	3	7		50	4	22		4		8	60	7
3	3	9		50	6	13	3	7		70	6	23		4		8	70	6,5
4	4	8		40	4	14	3	7		35	3	24		3		9	55	6
5	2	8		50	4	15	4	6		100	8	25		4		10	60	7
6	2	8		70	6	16	4	6		35	3	26		5		9	50	6
7	4	10		70	8	17	1	5		60	3	27		5		9	70	8
8	2	6		50	3	18	3	5		50	3	28		4		10	70	8
9	2	8		80	6,5	19	3	7		80	6,5	29		1		9	50	4
10	2	12		50	6	20	3	5		45	3	30		1		9	70	6

135

Задача	2.80.2. Время службы (в часах) каждого предохранителя
случайно и	имеет плотность вероятностиf (x) =1 – exp{-lx}, x ³ 0.

Перегоревший предохранитель практически мгновенно заменяется новым. Оценить вероятность того, что запаса n предохранителей хватит на m часов работы ( l = 0, 01 в вариантах 1–10; l = 0, 02 в вариантах 11–19; l = 0, 03 в вариантах 20–23; l = 0, 04 в вариантах 24–30). (См. пример 2.80 и исходные данные.)

Исходные данные к задаче 2.80.2.

№ n m № n m № n m № n m № n m

1	25	3000	7	55	6000	13	40	2500	19	70	3500	25	35	1000
2	30	3000	8	60	6000	14	45	2500	20	30	1000	26	40	1000
3	35	4000	9	65	7000	15	50	2500	21	45	1500	27	50	1300
4	40	4000	10	70	7000	16	55	3000	22	65	1750	28	55	1500
5	45	5000	11	25	1500	17	60	3000	23	75	2000	29	60	1500
6	50	5000	12	30	1500	18	65	3500	24	25	700	30	70	750

Пример 2.81. Жетон для игрального автомата стоит10 рублей. При использовании одного жетона (в отдельной игре) вероятность не получить ничего равна 0,8, вероятность получить 20 рублей равна 0,15, вероятность получения 50 рублей равна 0,04 и вероятность получения 100 рублей равна 0,01. Игрок купил жетонов на1000 рублей. Какова вероятность того, что игрок не окажется в проигрыше?

Решение. Игрок купил 1000 :10 =100 жетонов. Результат каждой игры (использование одного жетона) является случайной величиной Xi с законом распределения

Xi

–10

10

40

90

Выигрыш

P

0,8

0,15

0,04

0,01

указан с

учетом

стоимости

жетона

.

Y

Результат 100 игр обозначим через Y = X1 + X 2 +K+ X100 . Величина

является

суммой

большого

числа

одинаково

распределенны

независимых случайных величин, каждая из которых ограничена. По центральной предельной теореме Y имеет закон распределения близкий к нормальному закону распределения. Найдем параметры этого закона, т.е. математическое ожидание и дисперсию величиныY. Так как случайные величины Xi независимы, то

М (Y ) = М ( X1 ) + М ( X 2 ) +¼+=М ( X100 ) и D(Y ) D( X1 ) + D( X 2 ) +¼+ D( X100 ).

Так как
М ( X i ) = -10 ×0,8 +10 × 0,15 + 40 ×0,04 + 90 ×0,01=	-2,

а D( Xi ) = (-10 + 2)2 × 0,8 + (10 + 2)2 ×0,15 + (40 + 2)2 ×0,04 + (90 + 2)2 ×0, 01= 228,

то М (Y ) = -2 ×100= -200, D(Y ) = s2 (Y )= 228 ×100 = 22800, s(Y ) »151.

136

Итак, Y	имеет	примерно		нормальный				закон		распределения
N (-200; 22800). Игрок не окажется в проигрыше,						если Y ³ 0. По формуле
(2.9.2) имеем			9000 - (-200)			æ 0 - (-200)
		æ			ö				ö
P(Y ³ 0)	P(0 £ Y £=9000) Fç		=		÷	- Fç			÷	=
				151				151
		è			ø	è			ø
	= F(61) - F(1,32)		0,5 – =0, 4066 » 0,09.

Ответ. » 0,09.

Задача 2.81. Лотерейный билет стоит 20 рублей. С вероятностью p1 билет окажется без выигрыша, с вероятностью p2 на билет выпадет выигрыш ценой 100 рублей и с вероятностьюp3 билет выиграет выигрыш ценой 200 рублей. Какова вероятность остаться в проигрыше, если приобрести n билетов? (См. пример 2.81 и исходные данные.)

Исходные данные к задаче 2.81.

№	p1	p2	p3	n	№	p1	p2	p3	n	№	p1	p2	p3	n
1	0,9	0,08	0,02	20	11	0,9	0,06	0,04	25	21	0,9	0,08	0,02	45
2	0,9	0,07	0,03	60	12	0,9	0,09	0,01	40	22	0,9	0,07	0,03	30
3	0,9	0,06	0,04	20	13	0,9	0,08	0,02	35	23	0,9	0,06	0,04	45
4	0,9	0,09	0,01	50	14	0,9	0,07	0,03	40	24	0,9	0,09	0,01	35
5	0,9	0,08	0,02	30	15	0,9	0,06	0,04	35	25	0,9	0,08	0,02	50
6	0,9	0,07	0,03	50	16	0,9	0,09	0,01	20	26	0,9	0,07	0,03	25
7	0,9	0,06	0,04	30	17	0,9	0,08	0,02	40	27	0,9	0,06	0,04	50
8	0,9	0,09	0,01	45	18	0,9	0,07	0,03	35	28	0,9	0,09	0,01	30
9	0,9	0,08	0,02	25	19	0,9	0,06	0,04	40	29	0,9	0,08	0,02	60
10	0,9	0,07	0,03	45	20	0,9	0,09	0,01	25	30	0,9	0,07	0,03	20

Пусть k / n –– частота появлений события в n независимых опытах, в каждом из которых вероятность появления события равна( 0 < р <1). Тогда при достаточно большихn (порядка десятков, сотен и т..д) для любого 0 < a имеют место следующая формула

æ

ç

P(| k / n – р |< a) » 2Fç

ç

ç

è

где Ф –– функция Лапласа.

		ö
	a	÷
			÷,	(2.13.1)

pq ÷

÷

n ø

Пример 2.82.1. Вероятность рождения мальчика равна0,514. Определить вероятность ,тогочто доля мальчиков среди400 новорожденных будет отличаться от вероятности рождения мальчика не более чем на 0,05 в ту или другую сторону.

137

Решение. Рождение ребенка можно рассматривать как независимый опыт с вероятностью «успеха» p = 0,514 (по данным статистики на каждую тысячу новорожденных приходится514 мальчиков). Тогда по формуле

(2.13.1)

	æ		0, 05	ö
	Р(| k / n – 0,514| < 0,=05) 2Fç	=		÷ 2F(2,=0004) 0,9545.
			0,514 ×0, 486 / 400
	è			ø

Ответ. 0,9545.

Пример 2.82.2. Вероятность событияP( A) = p = 0,9. Сколько независимых опытов нужно проделать, чтобы с вероятностью0,95 быть уверенным, что частота появления события в этих опытах будет отличаться от вероятности события не более чем на 0,05 в ту или другую сторону?

Решение. Запишем формулу (2.13.1) для нашего случая:

æ		k			ö	æ			0,05	ö
P ç			- 0,9	< 0,05	÷	2F ç		=		÷	= 0,95.
		n
è					ø	è		0,9 ×0,1 / n ø

По таблице функции Лапласа находим, что 2F(1,96) = 0,95. Поэтому

0,05×0,05 × 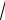n / 0,3 =1,96. Откуда n »138,3. Условия задачи выполняются при n ³139.

Ответ. n ³139.

Задача 2.82. Монету подбрасывают n раз. Какова вероятность того, что частота выпадения гербабудет отличаться от вероятности выпадения герба не более, чем на a в ту или другую сторону. Сколько раз нужно подбросить монету, чтобы с вероятностью P можно было утверждать, что частота выпадения герба будет отличается от вероятности выпадения герба не более чем на a в ту или другую сторону? (См. примеры 2.82.1, 2.82.2 и исходные данные.)

Исходные данные к задаче 2.82.

№	n	a	P	№	n	a	P	№	n	a	P
1	256	0,02	0,9	11	841	0,03	0,97	21	400	0,03	0,95
2	289	0,01	0,95	12	900	0,05	0,98	22	441	0,06	0,96
3	324	0,03	0,96	13	961	0,10	0,99	23	484	0,10	0,97
4	361	0,05	0,97	14	1024	0,03	0,90	24	576	0,10	0,99
5	400	0,04	0,98	15	1225	0,04	0,95	25	676	0,04	0,95
6	484	0,03	0,99	16	1600	0,02	0,96	26	729	0,10	0,96
7	576	0,05	0,90	17	256	0,04	0,97	27	641	0,10	0,98
8	676	0,02	0,95	18	289	0,03	0,98	28	900	0,10	0,95
9	729	0,05	0,96	19	324	0,02	0,99	29	961	0,10	0,999
10	784	0,02	0,97	20	361	0,04	0,90	30	1024	0,04	0,99

138