3. Нахождение оптимального решения методом множителей Лагранжа

Сначала убедимся в том, что задача (1) – (3) является задачей выпуклого программирования (ВП). Действительно, все ограничения задачи линейны, а ЦФ — выпуклая функция, как сумма выпуклых функций f₁(x₁) и f₂(x₂).

Чтобы применить метод множителей Лагранжа для решения задачи, следует отбросить условие неотрицательности переменных (3). Тогда исходная задача может быть переформулирована следующим образом: найти неизвестные значения переменных х₁ и х₂, доставляющие минимальное значение функции

Z = 40 + 2 x₁+ 0.2 + 6 x₂+ 0.3 → min (6)

и удовлетворяющие условию

х₁ + х₂ = 100. (7)

Ясно, что эта задача также является задачей ВП. Отказ от условия (3) приводит к расширению ОДР, так что оптимальное решение задачи (6) – (7) может оказаться недопустимым в исходной задаче (1) – (3). Однако очевидно, что если оптимальное решение задачи (6) – (7) удовлетворяет условию неотрицательности, то это решение будет оптимально и в исходной задаче.

Построим функцию Лагранжа задачи (6) – (7) по формуле (8). Она имеет вид

L(x₁, x₂, λ) = 40 + 2 x₁+ 0.2 + 6 x₂+ 0.3 + λ (100 – х₁ – х₂). (8)

Найдем частные производные функции L по x₁, x₂ и λ, а затем приравняем их к нулю. Получим следующую систему уравнений:

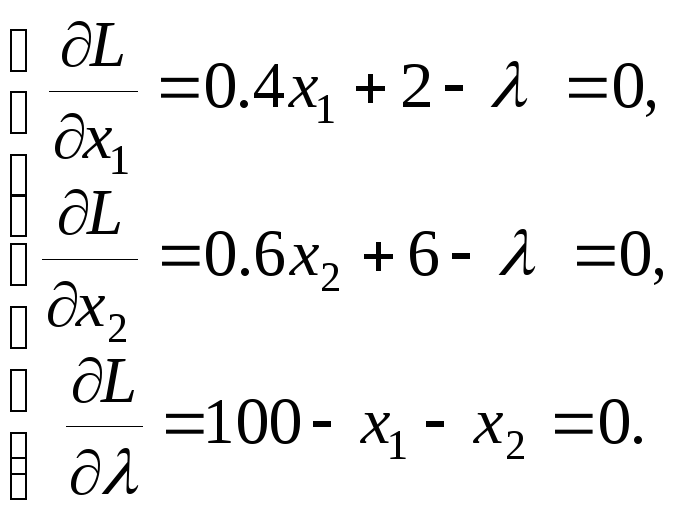(9)

Исключим переменную λ, вычтя из первого уравнения второе. Тогда получим систему уравнений:

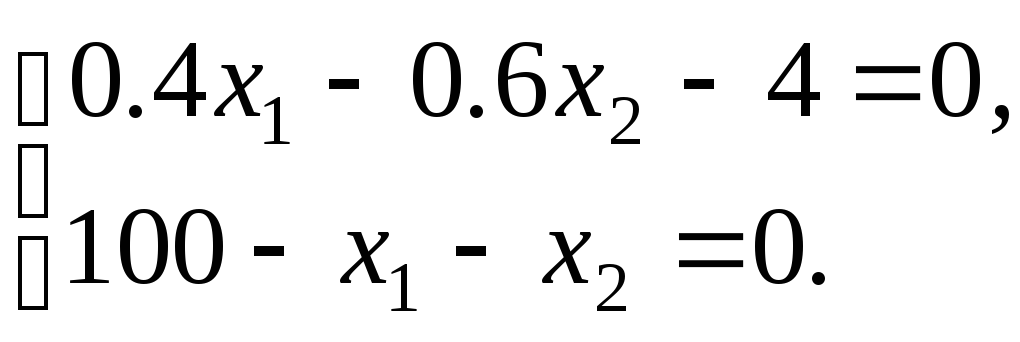(10)

Она фактически совпадает с системой (5) и, значит, имеет такое же решение: = 64 и = 36. Поскольку задача (6) – (7) является задачей ВП, то вектор х^* = (,) = (64, 36) является ее оптимальным решением. Так как найденное решение удовлетворяет условию неотрицательности, то оно будет оптимальным в исходной задаче (1) – (3).

Итак, методом множителей Лагранжа получено оптимальное решение, совпадающее с решением, полученным ранее графическим методом: предприниматель должен распределить заказ между фирмами следующим образом: заказать первой фирме 62 изделия, а второй фирме — 36 изделий. В этом случае его затраты будут минимальными и составят 1592 руб.

Из первого уравнения в системе (9) легко найти оптимальное значение множителя Лагранжа: λ^* = 0.4×64 + 2 = 27.6 (руб./ед.).

Множитель Лагранжа λ^* имеет такую экономическую интерпретацию: его величина приближенно показывает насколько возрастут минимальные общие затраты Z^*(d), если величина заказа d увеличится на единицу, т.е.

λ^* ≈ ΔZ^*(d) = Z^*(d + 1) – Z^*(d).

Таким образом, при увеличении заказа от 100 ед. до 101 ед. затраты возрастут примерно на 27.6 руб.

Замечание 1. Точное значение прироста затрат несколько выше: оно равно 27.72 руб. Его можно получить, решив задачу 1 для d = 101. Для этого достаточно найти решение системы, аналогичной (10), в которой второе уравнение имеет следующий вид: 101 – х₁ – х₂ = 0.

Замечание 2. Решение задачи 1 можно свести к отысканию минимума функции одной переменной на заданном отрезке. Для этого достаточно выразить одну из переменных через другую, используя уравнение (2), а затем подставить полученное выражение в формулу (1), определяющую ЦФ. Однако этот упрощающий прием возможен лишь потому, что ограничение в задаче имеет очень простой вид, и не применим в общем случае. Универсальным способом решения оптимизационных задач с ограничениями типа равенства является метод множителей Лагранжа.