Подчипаев Д.О._к семинару

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление пр едикатов. Применение предикатов в математической практике.

Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова («все», «су ществует» и другие), называемые в логике кванторами.

Кванторы в математ ической логике

∙ Высказывание		означает, что область значений переменной				включена
в область истинности п редиката				.
(«При всех значениях		утверждение верно»).

∙Высказывание означает, что область истинн ости предиката непуста.

(«Существует при ко тором утверждение верно»).

Операции над кванторами

Правило отрицания кванторов — применяется для п остроения отрицаний высказываний, содержащих кванторы, и имеет вид:

1.Квантор всеобщ ности.

Пусть Р(х) – предикат, определенный на множестве М. Под выражением

понимают высказывание, истинное, когда Р(х) истинно для каждого элемента х из множества М, и ложное в противном случае. Это высказывание уже не зависит от х. Соответствующее ему словесное выражение звучит так: “ Для всякого х Р(х) истинно

”.

Символ называют квантором всеобщности (общности). Переменную х в

предикате Р(х) называют свободной (ей можно придавать разли чные значения из М), в

высказывании же х называют связанной квантором всеобщности.

2.Квантор существования.

Пусть P(x) - предикат определенный на множестве М. Под выражением понимают высказывание, ко торое является истинным, если сущ ествует элемент ,

для которого P(x) истинно, и ложным – в противном случае. Эт о высказывание уже не зависит от x. Соответствую щее ему словесное выражение звуч ит так: “ Существует x,

11

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление предикатов. Применение предикатов в математической практике.

при котором P(x) истинно.” Символ называют квантором существования. В

высказывании переменная x связана этим квантором (на нее навешен квантор).

Кванторные операции применяются и к многоместным предикатам. Пусть,

например, на множестве М задан двухместный предикат P(x,y). Применение кванторной операции к предикату P(x,y) по переменной x ставит в соответствие двухместному предикату P(x,y) одноместный предикат (или одноместный предикат ), зависящий от переменной y и не зависящий от переменной x. К

ним можно применить кванторные операции по переменной y, которые приведут уже к высказываниям следующих видов:

Рассмотрим предикат P(x) определенный на множестве M={a1,…,a n},

содержащем конечное число элементов. Если предикат P(x) является тождественно -

истинным, то истинными будут высказывания P(a1),P(a2),…,P(a n). При этом истинными

будут высказывания

и конъюнкция

.

Если же хотя бы для одного элемента

P(ak)окажется ложным, то ложными

будут высказывание

и конъюнкция

. Следовательно, справедлива

равносильность

.

Численные кванторы.

В математике часто встречаются выражения вида “ по меньшей мере n” (“ хотя бы

n”), “ не более чем n”, “n и только n” (“ ровно n”), где n – натуральное число.

Эти выражения, называемые численными кванторами, имеют чисто логический смысл; они могут быть заменены равнозначными выражениями, не содержащими

числительных и состоящими только из логических терминов и знака или ~,

означающего тождество (совпадение) объектов.

Пусть n=1. Предложение “ По меньшей мере один объект обладает свойством P”

имеет тот же смысл, что и предложение “ Существует объект, обладающий свойством

P”, т.е.						(*)
		12

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление предикатов. Применение предикатов в математической практике.

Предложение “ не более чем один объект обладает свойством P” равнозначно предложению “ Если есть объекты, обладающие свойством P, то они совпадают”, т.е. (**) Предложение “ один и только один объект обладает свойством P” равнозначно конъюнкции вышеуказанных предложений (*) и (**).

3.Отрицание предложений с кванторами.

Известно, что часто для отрицания некоторого предложения достаточно предпослать

сказуемому этого предложения отрицательную частицу “ не”. Например, отрицанием предложения “ Река х впадает в Черное море.” является предложение “ Река х не впадает в Черное море”. Годится ли этот прием для построения отрицаний предложений с кванторами? Рассмотрим пример.

Предложения “ Все птицы летают ” и “ Все птицы не летают ” не являются отрицаниями друг друга, т. к. они оба ложны. Предложения “ Некоторые птицы

летают ” и “ Некоторые птицы не летают ” не являются отрицанием друг друга, т. к.

они оба истинны. Таким образом , предложения , полученные добавлением частицы

“ не” к сказуемому предложений “ Все х суть Р” и “ Некоторые х суть Р” не являются отрицаниями этих предложений. Универсальным способом построения отрицания

данного предложения является добавление словосочетания “ наверно, что” в начале предложения. Таким образом, отрицанием предложения “ Все птицы летают” является предложение “ Неверно, что все птицы летают”; но это предложение имеет тот же

смысл, что и предложение “ Некоторые птицы не летают”. Отрицанием предложения

“ Некоторые птицы летают”

является предложение “ Неверно, что некоторые птицы

летают”, которое имеет тот же смысл, что и предложение “ Все птицы не летают”.

, а отрицание

Условимся отрицание предложения

записывать как

– как

. Очевидно, что предложение

предложения

имеет

тот же смысл, а

следовательно, то

же значение истинности,

что

и

предложение

, а предложение

– тот же смысл, что

.

Иначе говоря,

;

.

равносильно

равносильно

13

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление пр едикатов. Применение предикатов в математической практике.

Кванторы общности и существования называют двойственными относительно друг друга. Выясним теперь , как строить отрицание предложения, начинающегося с

нескольких кванторов, напри мер, такого:

.

правило, получим:

Последовательно при меняя сформулированное

выше

рав носильно

,

что

равносильно

, что равносильно

.

Исчисление предикатов Логика первого порядка (исчисление предикатов) — фо рмальное исчисление,

допускающее высказывания относительно переменных, фикси рованных функций и предикатов. Расширяет логику высказываний. В свою очер едь является частным случаем логики высшего порядка.

Основные определени я

Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов и множества предикатных символов . С

каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные, так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант.

Кроме того, используются следующие дополнительные символы

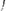
∙Символы переменных (обычно и т. д.),

∙Пропозициональные связки: ,

∙Кванторы: всеобщности и существования ,

∙Служебные символы: скобки и запятая.

Перечисленные символы вместе с символами из и образуют Алфавит логики первого порядка. Б олее сложные конструкции определ яются индуктивно:

∙Терм есть символ переменной, либо имеет вид , где —

функциональный символ арности , а — термы.

∙ Атом имеет вид , где — предикатный символ арности , а

— термы.

14

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление пр едикатов. Применение предикатов

в математической практике.

∙

Формула — это либо атом,

либо одна

из след ующих конструкций:

,

где

—

формулы, а

—

переменная.

Переменная называется связанной в формуле , если имеет вид либо

, или же представима в одной из форм , причем уже связана в 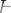, и . Если не связанна в , ее назы вают свободной в .

Формулу без свободных переменных называют замкнутой формулой, или

предложением. Теорией первого порядка называют любое множе ство предложений.

Интерпретация

В классическом случае интерпретация формул логики пер вого порядка задается на модели первого порядка, которая определяется следующими данными

∙Несущее множество ,

∙Семантическая функция , отображающая

o

каждый

-арный функциональный символ

из

в n-арную функцию

,

n-арны й предикатный символ

в n-арное отношение

o

каждый

из

.

Обычно принято, отождествлять несущее множество

и саму модель,

подразумевая неявно семантическую функцию, если это не веде т к неоднозначности.

Предположим

— функция, отображающая каждую переменную в некоторый

элемент из

,

которую мы б удем называть подстановкой. Интерпретация

терма

на

относительно подстановки

задается индуктивно

∙

, если —

переменная,

∙

В таком

же

духе определяется отношение истинност и

формул на

относительно

∙

∙

∙

, тогда и только тогда, когда

,

, тогда и только тогда, когда

— ложно,

, тогда и только тогда, когда

истинны,

и

15

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление пр едикатов. Применение предикатов

вматематической практике.

∙, тогда и только тогда, когда или истинно,

∙

, тогда и только тогда, когда

влечет

,

∙

,

тогда и только тогда, когда

для

некоторой

подстановки

, которая

отличается от только на переменной

,

∙, тогда и только тогда, когда для всех подстановок ,

которые отличается от тол ько на переменной .

Формула

, истинна на , что обозначается как

, если

, для всех

подстановок . Формула

называется общезначимой,

что обозн ачается как

, если

для всех моделей

. Формула

называется выполнимой , если

хотя бы

для одной

.

Свойства и основные результаты

Логика первого порядка обладает рядом полезных свойс тв, которые делают ее очень привлекательной в ка честве основного инструмента форм ализации математики.

Главными из них являются полнота (это означает, что для любо й замкнутой формулы выводима либо она сама, либо ее отрицание) и непротиворечивость (ни одна формула не может быть выведена одновременно со своим отрицанием). При этом если непротиворечивость более или менее очевидна, то полно та — нетривиальный результат.

Логика первого пор ядка обладает свойством компакт ности: если некоторое множество формул не вып олнимо, то невыполнимо также некоторое его конечное подмножество.

Логика первого поря дка как формальная модель рассуждений

Являясь формализованым аналогом обычной логики, логика первого порядка

дает возможность строго ра ссуждать об истинности и ложност и утверждений и об их взаимосвязи, в частности, о логическом следовании одного утверждения из другого,

или, например, об их эквивалентности. Рассмотрим к лассический пример формализации утверждений естественного языка в логике перв ого порядка.

Возьмем рассуждение «Каждый человек смертен. К онфуций — человек. Следовательно, Конфуций смертен». Обозначим «x есть человек» через ЧЕЛОВЕК(x)

16

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление пр едикатов. Применение предикатов

вматематической практике.

и«x смертен» через СМЕР ТЕН(x). Тогда утверждение «каждый человек смертен» может быть представлено формулой: x(ЧЕЛОВЕК(x) → СМЕРТЕН(x)) утверждение «Конфуций — человек» формулой ЧЕЛО ВЕК(Конфуций), и «Конфуций смертен» формулой СМЕРТЕН(Конфуций). Утверждение в целом теперь

может быть записано форму лой

( x(ЧЕЛОВЕК(x) → СМЕРТЕН(x))

ЧЕЛОВ ЕК(Конфуций)) →

СМЕРТЕН(Конфуций)

Применение логики предикатов

Умение грамотно оперировать языком логики является основой современной

логической культуры.

Важнейшей сферой применения логики предикатов к логико-математической

практике является сфер а построения доказательств различных теорем,

основывающаяся на теории логического следования. Более сло жное строение формул логики предикатов, по сравнению с формулами логики высказываний, дает возможность проводить более сложные доказательства и в результате получать более тонкие заключения.

С помощью кванторной символики удобно записывать фо рмулировки различных

определений и теорем. В процессе такой записи приходится осмысливать данное

предложение, отчетливо выявлять в нем посылки и следствие (если это теорема),

очерчивать более широкий круг понятий и четко выявлять ограничивающее условие

(если это определение). Одним словом, перевод расп лывчатой словесной

формулировки на строгий, не допускающий противоречивых толкований язык логики предикатов способствует четкости и ясности мышления.

Рассмотрим некоторые примеры:

Пример 1. Определение предела последовательности "Число а называется

пределом последовательности		,	если для всякого положи тельного числа
существует такое натуральное число					, что для всякого натурального		, большего

" на языке логики предикатов записывается так:

17

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление предикатов. Применение предикатов в математической практике.

Используя символику ограниченных кванторов, это определение можно записать компактнее:

Пример 2. Запишем на языке логики предикатов определение простого числа: "Натуральное число называется простым, если оно не равно 1 и при всяком разложении его в произведение двух натуральных чисел одно из них оказывается равным 1 или ":

Отрицание этого утверждения — утверждение того, что число составное,

записывается следующим образом:

Пример 3. Определение "Точка из области определения функции называется точкой локального максимума функции 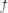, если существует такая ∞малая окрестность данной точки, что для всех из этой окрестности " на языке логики предикатов запишется так:

Пример 4. Этот пример более наглядно демонстрирует выразительные возможности языка логики предикатов по сравнению с языком логики высказываний.

Рассмотрим два высказывания: "В Москве живет женщина, имеющая брата в Петербурге" и "В Петербурге живет мужчина, имеющий сестру в Москве". Каждое из данных утверждений следует из другого, т.е. они равносильны. Спрашивается, можно ли выразить эту равносильность на языке алгебры высказываний, на языке логики предикатов? Оказывается второе возможно, а первое нет.

В самом деле, как мы могли бы формализовать данные высказывания на языке алгебры высказываний? Можно обозначить первое высказывание через , второе — через . Ясно, что ни о какой равносильности формул и говорить не приходится.

Можно расчленить данные высказывания на более простые: — " Женщина живет в Москве"; — " Женщина имеет брата в Петербурге"; — " Мужчина живет в Петербурге"; — " Мужчина имеет сестру в Москве". Тогда первое исходное

18

Подчипаев Д.О.

Отношения. Высказывания. Предикаты. Унарные и бинарные предикаты. Кванторы. Исчисление предикатов. Применение предикатов

	в математической практике.
высказывание есть конъюнкция					, а второе —		. Но и эти две формулы

алгебры высказываний не следуют одна из другой.

В отличие от алгебры высказываний, формализация на языке логики предикатов позволяет обнаружить равносильность двух данных высказываний. Действительно,

введем предикаты, определенные на множестве людей:

— "

—

женщина";

— "

живет в Москве";

— "

—

мужчина";

— "

живет в

Петербурге;

— "

есть сестра

".

Тогда высказыванию "В Москве живет

женщина, имеющая брата в Петербурге" соответствует формула логики предикатов

а высказыванию "В Петербурге живет мужчина, имеющий сестру в Москве" —

формула

Покажем, что полученные формулы равносильны, для чего первую из них равносильными преобразованиями сведем ко второй (предлагается обнаружить те равносильности логики предикатов, которые используются на каждом шаге преобразований):

19

Подчипаев Д.О.