Конспект лекций по ТАУ

C

η

= С

e−ηt

= e−ηt

η

1

ηt

1

= ln(e

) = ln

eηt

t =

1

1

ln

.

η

Эта формула позволяет оценить время переходного процесса tП.

При = 0,05 получаем

t		=	1	ln	1	≈	3	.
	П				0,05
			η				η

Если ближайшей к мнимой оси является пара ком- плексно-сопряженных корней η ± j β, то их составляющая в переходном процессе описывается формулой вида

yη (t) = Cηe− ηt sin(βt + ψ).

Здесь можно найти верхнюю границу времени переходного процесса, приняв условие sin(βt + ψ)=1, тогда

tр ≤ η3 .

Запас устойчивости системы оценивается колебательностью. Система имеет склонность к колебаниям, если характеристическое уравнение содержит ком-

плексные корни η1,2= -α ± j β. Колебательность оценивается по формуле

131

µ = βα .

Если система имеет несколько комплексносопряженных корней, то ее колебательные свойства определяет пара комплексных корней, для которой µ принимает наибольшее отношение.

Затухание является еще одной характеристикой переходного процесса. Комплексные корни дают в переходном процессе составляющую

y(t) = Ce−αt sin(βt + ψ).

В момент t1 амплитуда колебаний

C1 = Ce−αt1 .

Период колебаний

T = 2βπ .

Амплитуда колебаний через период

		−α(t1	+	2π	)	−2π	α	−	2π
C
	2	= Ce		β		= C e	β	= C e µ .
						1		1

Затуханием за период называют величину

ε = C1 − C2 = 1− C1 = 1− e− 2µπ .

C1 C2

Таким образом

132

µ =		2π			.
	ln	1
			1− ε

Например, если задано значение затухания за период 90%, то допустимое значение колебательности

µ = 2,73.

По значению колебательности можно приближенно оценить перерегулирование

− π

δ £ e µ ×100%.

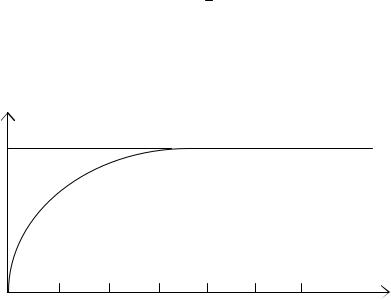
Пример 3.6. По переходному процессу y(t) (рис. 3.6) на ступенчатый сигнал вида u(t) = 4*1[t] определить передаточную функцию динамического звена.

y(t)

6

0 1 2 3 4 5 6 t, с

Рис. 3.6. Реакция на ступенчатое входное воздействие.

133

Решение.

Кривая переходного процесса соответствует инерционному звену с ПФ:

W =	k
		.
	Ts + 1

Коэффициент усиления k определяется по графику:

	k =	yуст	=	6	= 1,5.
		g		4

Используя формулу для оценки времени переходного процесса, имеем

	t	≈	3	η ≈ 1.
			η
	р

Окончательно получаем

= 1,5

W s + 1.

Пример 3.7. Система описывается ПФ

= 2,5

W (2s + 1)(3s + 1).

Чему равна длительность переходного процесса? Решение. Система имеет два полюса: λ1= –0,5 и λ2= –

0,33, таким образом, получаем

	η =				− 0.33					;
	t		≈			3	=	3			≈ 9.
		р				η		0.33

134

1.Выбор параметров регулятора

Вразделе 1.5 были описаны принципы экспериментальной настройки регуляторов по отклонению, которые не требуют использования математического описания объекта управления. Если же математическое описание известно, то настройка регулятора может быть выполнена более точно на основании требований

красположению полюсов замкнутой системы. Рассмотрим работу ПИ-регулятора. Пусть объект

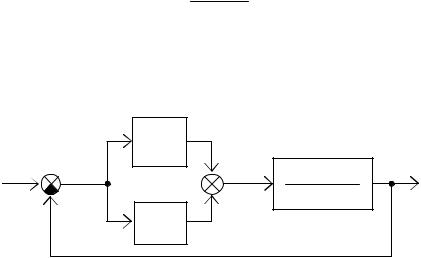
управления описывается с помощью ПФ первого порядка, где a > 0 и b – известные константы (рис. 3.7).

		K I
		s
R(s)	E(s	U(s	1	Y(s)
			sa + b
		Kp

Рис. 3.7. Система управления с ПИ-регулятором

Задача управления заключается в обеспечении условия: y(t) → r, при t → ∞ (где r – заданное значение входного сигнала (уставка)).

В соответствии с рис. 3.7:

135

U (s) = K	E(s) +			KI	E(s),
P				s
E(s) = R(s) − Y (s),
	1
Y (s) =			U (s).
		as + b

Передаточная функция разомкнутой системы

	Kp s + KI		1
Н(s) =					=
	s
		as + b

Kp s + KI . as2 + bs

Обозначим через W(s) передаточную функцию замкнутой системы, тогда

			KP s + KI
Y (s) = W (s)R(s) =
		2
			+ (b + KP )s + KI
as

R(s).

Система имеет два полюса

	=	− (b + KP )±			.
s			(b + Kp )2 − 4aKI
1,2			2a

Отрицательность вещественной части полюсов гарантируется условием: Kp + b > 0 или Kp > – b.

Для получения на выходе системы заданного значения r, требуется обеспечить

lim e(t) = 0.

t →∞

В соответствии с теоремой о конечном значении:

136

lim e(t)

t →∞

= lim s

s →∞

= lim sE(s) = lim s(R(s) − Y (s)) =
s	→∞		s	→∞
			as2 + bs			r
					×			= 0.
	2
as		+ (b + Kp )s + KI
						s

Это условие выполняется при любом KI. Для обеспечения апериодичности переходного процесса можно потребовать, чтобы мнимая часть полюсов была равна нулю, тогда:

(b + Kp )2 − 4aKI = 0.

KI = (b + Kp )2 . 4a

Рассмотрим работу далее ПД-регулятора. Пусть объект управления описывается с помощью ПФ 2-го порядка, где a > 0, b и с – известные константы (рис. 3.8).

sKd

R(s)	E(s	U(s	1	Y(s)
			as2 + bs + c
		Kp

Рис. 3.8. Система управления с ПИ-регулятором

В соответствии с рис. 3.8

137

U (s) = KP E(s) + Kd sE(s),

E(s) = R(s) − Y (s),

Y (s) = 1 U (s). as2 + bs + c

Обозначим через W(s) передаточную функцию замкнутой системы, тогда

Y (s) = W (s)R(s) =				KP + Kd s	(c + Kp )	R(s).
			as2 + (b + Kd )s +
Система имеет два полюса:
	=	− (b + Kd ) ±						.
s				(b + Kd )2 − 4a(c + Kp )
1,2				2a

Отрицательность вещественной части полюсов гарантируется (при a > 0) условием: Kd + b > 0 или Kd > –

b.

Для обеспечения апериодичности переходного процесса можно потребовать, чтобы мнимая часть полюсов была равна нулю, тогда:

(b + Kd )2 − 4a(c + Kp )= 0,

Kp = (b + Kd )2 − c. 4a

Для получения на выходе системы заданного значения r, требуется обеспечить

lim e(t) = 0.

t →∞

138

В соответствии с теоремой о конечном значении:

lim e(t)

t →∞

= lim s

s →∞

= lim sE(s) = lim s(R(s) − Y (s)) =
s →∞	s →∞
	as2 + bs + c		r			cr
as2 + (b + Kd )s + (c + Kp )× s					= c + Kp .

Таким образом, в системе присутствует установившаяся ошибка.

Задача регулятора заключается в обеспечении заданного расположения полюсов замкнутой системы.

Выбирать положение полюсов можно, опираясь на корневые оценки качества системы. Один из возможных подходов заключается в обеспечении одинаковости всех корней характеристического уравнения. Каждый корень λ должен быть отрицательным, а величина его модуля λ0 определяется требованиями к быстродействию. Левая часть характеристического уравнения обращается в бином Ньютона (s + λ0)n, разворачивая который, можно получить стандартные значения коэффициентов характеристического уравнения. Биномиальные стандартные формы для систем до четвертого порядка имеют вид:

s + λ0 ,

s2 + 2λ0 s + λ02 ,

s3 + 3λ0s2 + 3λ02s + λ30 ,

s4 + 4λ0 s3 + 6λ02s2 + 4λ30 s + λ04 .

При таком подходе обеспечивается апериодичность переходного процесса.

139

Существуют и другие стандартные формы, например форма Баттерворта, в соответствии с которой корни должны располагаться в левой полуплоскости на окружности радиуса λ на одинаковых угловых расстояниях друг от друга (рис. 3.9).

Im

-λ	0	Re

Рис. 3.9. Распределение Баттерворта для системы 4-го порядка.

Стандартные формы Баттерворта для систем до четвертого порядка имеют вид:

s + λ0 ,

s2 + 1.4λ0 s + λ02 ,

s3 + 2λ0s2 + 2λ02 s + λ30 ,

s4 + 2.6λ0 s3 + 3.4λ02s2 + 2.6λ30 s + λ04 .

140