Конспект лекций по ТАУ

dy(t)/dt	sY(s) – y(0)
d2y(t)/dt2	s2Y(s) – sy(0) – dy(0)/dt
dny(t)/dtn	snY(s) – sn-1y(0) – sn-2dy(0)/dt … – s0dn-1y(0)/dtn-1

Таким образом, при нулевых начальных условиях справедли-

во:
		n	y(t)
L	d				= s nY (s)
		dt n

3) Интегрирование оригинала. Эта операция сводится к делению изображения на s:

	t			Y (s)
	L ∫ x(t)dt		=
				s
	0

4)Теорема запаздывания. Для любого положительного числа

τсправедливо:

L{y(t −τ )}= e− sτ L{y(t)} = e− sτ Y (s) .

Таким образом, функции y(t) и y(t – τ) описывают один и тот же процесс, но процесс, описываемый функцией y(t – τ), начинается с опозданием на время τ. В области изображений это соответствует умножению на e-sτ.

5) Теорема умножения изображения. Если y1(t) и y2(t) – оригиналы, а Y1(s) и Y2(s) – их изображения, то

t t

Y1(s)Y2 (s) ≡ ∫ y1 (τ) y2 (t − τ)dτ =∫ y2 (τ) y1 (t − τ)dτ =y2 (t) * y1 (t),

0 0

где * - обозначение операции свертки.

51

6) Теорема о предельном значении. Если y(t) – оригинал, а Y(s) – его изображение, то

x(∞) = lim x(t) = lim sX (s) .

t→∞ s→0

Последняя теорема, как будет показано ниже, используется для расчета установившей ошибки систем управления.

До начала эпохи массового использования компьютеров задача нахождения решения дифференциального уравнения вызывала большие трудности, и преобразование Лапласа являлось эффективным инструментом для решения этой задачи.

Решение дифференциального уравнения, полученное с помощью преобразования Лапласа, представляет собой рациональную дробь. Для выполнения обратного преобразования необходимо разложить это решение на простейшие дроби. Для выполнения этой операции необходимо найти корни характеристического полинома. Разложение выполняется по правилам:

1)если корень λ действительного типа, то ему соответствует дробь вида

A

s − λ ;

2)если корень λ действительного типа имеет кратность n, то ему соответствует сумма дробей:

A		sA		sn−1 A
1	2			n
s − λ	+	(s − λ)2	+ ... +	(s − λ)n	;

3)паре комплексно-сопряженных корней соответствует дробь вида

A1s + B ; s2 + as + b

4)комплексно-сопряженным корням кратности n соответствует сумма дробей:

52

	A1s + B1			A2 s + B2			An s + Bn
		+	(s2 + as + b)2		+ ...	+	(s2 + as + b)n	.
	s2 + as + b
Пример 2.1. Дано дифференциальное уравнение
		&&		&
		2x		+ 6x + 4x = 1(t) ,
и начальные условия:		x(0) = 1; x(0) = 3.				Требуется определить
				&

x(t).

Решение.

На первом шаге записываем уравнение в изображениях:

2(s2 X (s) − s − 3)+ 6(sX (s) −1)+ 4 X (s) = 1 .

s

На втором шаге определим x(s):

= 2s2 + 12s + 1 = s2 + 6s + 0.5

X (s) s(2s2 + 6s + 4) s(s2 + 3s + 2).

Знаменатель имеет три различных корня действительного типа: s1 = 0, s2 = –2, s3 = –1, поэтому можно записать:

	s2 + 6s + 0.5		A		B		C
X (s) =	s(s2 + 3s + 2)	=		+		+		.
			s		s + 2		s + 1

Откуда следует

s2 + 6s + 0.5 = A(s + 2)(s + 1) + Bs(s + 1) + Cs(s + 2).

Приравнивая значения при одинаковых степенях s, получаем систему трех уравнений:

1 = A + B + C

	= 3A + B + 2C
6
	0,5 = 2 A

A = 0,25

= −

B 3,75.

C = 4,5

53

Таким образом
X (s) =	0,25		−	3,75	+	4,5		.
	s			s + 2 s + 1
Выполняя обратное преобразование, получаем:
x(t) = 0,25 ×1(t) - 3,75e−2t + 4,5e−t .
Пример 2.2. Дано изображение функции
X (s) =			s2 + 2
							.
		(s +1)3 (s − 2)

Знаменатель имеет корни действительного типа: s1 = 2 и s2 = – 1 с кратностью n = 3, поэтому можно записать:

	s2 + 2	A		A	A	A
X (s) = (s +1)3 (s − 2) = s +1				+ (s +1)2	+ (s +1)3	+ s − 2 .
		1		2	3	4

Откуда следует

s2 + 2 = A1 (s +1)2 (s − 2)+ A2 (s + 1)(s − 2)+ A3 (s − 2)+ A4 (s + 1)3.

				A1 + A4 = 0,
				A2 + 3A4 = 1,
		A − A − 3A + 3A = 0,
		3		2	1		4
	− 2A − 2A − 2A + A = 2.
		3			2		1 4
Решение этой системы дает ответ: А1 = –2/9,										A2 = 1/3, A3=–1,
A4 = 2/9.
X (s) =	s2 + 2		= −		2	+	1	−		1	+	2	.
				9(s +1)								2(s − 2)
	(s +1)3 (s − 2)						3(s +1)2		(s +1)3

54

−1

2

−t

1

−t

1

2

−t

2

2t

x(t) = L

( X (s)) = −

e

+

te

−

t

e

+

e

.

9

2

9

3

Пример 2.3. Найти оригинал по его изображению

F (s) =

2s − 5

.

s 2

− 6s +

11

Решение.

Преобразуем данную дробь: выделим в знаменателе дроби

полный квадрат и по свойству линейности получим

F (s) =

2s - 5

=

2(s - 3) +1

=

2(s - 3)

+

1

=

s2

- 6s +11 (s - 3)2 + 2 (s - 3)2 + ( 2)2

(s - 3)2 + ( 2)2

s - 3

= 2 ×

+

1

×

2

.

(s - 3)2 + ( 2 )2

2 (s

- 3)2

+ ( 2)2

Обратное преобразование Лапласа для этого выражения дает

решение:

f (t ) = 2e3t cos

t +

1

e3t

2

sin

2t.

2

2.2. Понятие передаточной функции

Передаточной функцией (ПФ) системы называется отношение преобразования по Лапласу выходной переменной к преобразованию по Лапласу входной переменной при нулевых начальных условиях:

y(s) = B(s) =

W (s) ,

x(s) A(s)

где s – комплексная переменная.

Степень полинома знаменателя называют порядком ПФ.

55

x1(s)

y(s) x2(s)

Можно также определить ПФ как отношение оператора воздействия к собственному оператору (оператор воздействия – дифференциальный оператор при входной переменной, собственный оператор – дифференциальный оператор при выходной переменной).

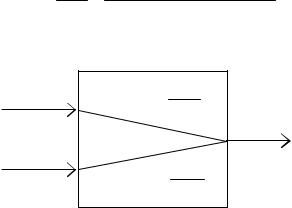
Если система имеет несколько входов, то при определении ПФ относительно какой-либо одной входной переменной остальные переменные полагают равными нулю (рис. 2.1).

Аналогично можно определить ПФ для объекта с несколькими входами и выходами.

Передаточную функцию линейной стационарной системы можно представить в виде

W (s) =

x1(s)

x2(s)

B(s) = bn (s − ν1 )(s − ν2 )...(s − νm ) , A(s) an (s − λ1)(s − λ2 )...(s − λn )

W (s)

= y(s)

1

y(s)

W2(s) =

Рис. 2.1. Передаточные функции объекта с двумя входами

Комплексные числа νi, являющиеся корнями многочлена B(s), называются нулями передаточной функции, а λi – корни много-

члена A(s) – полюсами.

56

W (s) =

Передаточная функция называется минимально-фазовой, если все ее нули и полюсы располагаются в левой полуплоскости, если же хотя бы один нуль или полюс располагается в правой полуплоскости, то ПФ – неминимально-фазовая.

Если ПФ имеет нуль или полюс на мнимой оси, то ее назы-

вают маргинальной.

Если известна ПФ системы и входной сигнал, то можно определить выходной сигнал:

y(s) = W (s)x(s).

Пример 2.4. Дано дифференциальное уравнение при нулевых начальных условиях:

3&y& + 2 y& + 6 y = 5x& + x.

Требуется найти соответствующую передаточную функцию.

Решение.

3s2 y(s) + 2sy(s) + 6 y(s) = 5sx(s) + x(s), y(s)(3s2 + 2s + 6) = x(s)(5s +1),

y(s) = 5s + 1

x(s) 3s2 + 2s + 6

.

Пример 2.5. Дана ПФ и описание входного сигнала:

W (s) =	1	;	x(t) = e-2t ×1(t).
	(s +1)(s + 3)

Определить выходной сигнал.

Решение.

	X (s) =	1		; Y (s) = W (s) X (s) =	1	.
		s +	2		(s +1)(s+2)(s + 3)

57

Знаменатель имеет три корня: s1 = –1,

s2 = –2, s3 = –3,

поэтому

можно записать:

1

A

B

C

Y (s) =

(s +1)(s + 2)(s + 3)

=

+

+

.

s + 1

s + 2

s + 3

Откуда следует

A(s + 2)(s + 3) + B(s + 1)(s + 3) + C(s +1)(s + 2) = 1,

A(s2 + 5s + 6) + B(s2 + 4s + 3) + C(s2 + 3s + 2) = 1.

Следовательно

As2 + Bs2 + Cs2 = 0,

A + B + C = 0,

A = 0.5,

= −1,

5As + 4Bs + 3Cs = 0,

5A + 4B + 3C = 0,

B

6 A + 3B + 2C = 1.

6 A + 3B + 2C = 1.

C = 0.5.

Таким образом:

1

0,5

1

0,5

y(s) =

(s + 1)(s + 2)(s + 3)

=

−

+

;

s + 1

s + 2

s + 3

y(t) = 0,5e−t − e− 2t + 0,5e−3t .

Пример 2.6. Дана ПФ и описание входного сигнала:

W (s) =	1	;	x(t) = 1(t) − 1(t − 2).
	(s + 1)(s + 3)

Требуется определить выходной сигнал.

Решение.

x(s) =	1	− e−2s	1	;
	s
			s
y(s) = W (s)x(s) =					1	(1	− e−2s ).
					s(s + 1)(s + 3)

58

1		1			1			1		1			- (t-2)	1			- 3(t - 2)
y(t) =		-		e-t	+		e- 3t 1(t) -			-		e		+		e		1(t − 2).
	3	2			6				3	2				6

Пример 2.7. Дана ПФ и описание входного сигнала:

W (s) =		20s2 + 180		x(t) = 2 sin(3t) + 1.
			;
	s3
		+ 9s2 + 27s + 27

Требуется определить установившийся выходной сигнал.

Решение.

X (s) =

1

+

6

.

s

s

2 + 9

Таким образом:

1

6

20s

2

+ 180

Y (s) = W (s) X (s) =

+

=

s

+ 9s 2 +

27s + 27

s 2 + 9

s3

+ 9)

=

1

+

6

20s 2

+ 180

=

20s 2

+ 180

+

6

20(s 2

=

(s

+ 9)

s

s

2

+ 9

(s + 3)

s(s + 3)

2

(s + 3)

3

3

3

=

20s 2

+ 180

+

120

=

20s 2

+ 120s + 180

.

s(s + 3)3

(s + 3)3

s(s + 3)3

Y (s) =

20s2 +120s +180

A

A

A

A

s(s + 3)3

= s + 3

+ (s + 3)2 +

(s + 3)3 +

s .

1

2

3

4

Откуда следует

20s2 +120s +180 = A1 (s + 3)2 s + A2 (s + 3)s + A3s + A4 (s + 3)3.

180 = 27A4 ,

120 = 9A + 3A + A + 27A ,

1

2

3

4

20 = 6A1 + A2

+ 27 A4 ,

A1 + A4 = 0.

59

Решение этой системы дает ответ: А1 = –6,66, A2 = –120, A3 = 360, A4 = 6,66.

20s2

+ 120s2 + 180

6.66

120

360

6,66

Y (s) =

= −

(s + 1)

−

+

+

.

s(s + 1)3

(s + 1)2

(s + 1)3

s

y(t) = L−1 (Y (s)) = -6,66e−t -120te−t + 360t 2e−t + 6,66 ×1(t).

Пример 2.8. Известно описание входного и выходного сигналов:

x(t) = 1(t), y(t) = 2e- 2t .

Требуется определить передаточную функцию.

Решение.
x(s) =	1	,	y(s) =	2		,	W (s) =	y(s)	=	2s	.
				s +	2
	s							x(s) s + 2

Рассмотрим, как получаются ПФ некоторых простейших схем

(см. рис. 2.2).

R	L		R
u	i	u1	C	u2
			i
а)			б)

Рис. 2.2. Простейшие электронные схемы

Для схемы на рис. 2.1, а будем считать входным сигналом приложенное напряжение u, а выходным – ток в цепи i. Тогда процессы в схеме описываются уравнением

60