Физика

чтобы нижняя кромка маятника была на 1–2 мм ниже оптической оси нижнего фотодатчика. Ось маятника должна быть горизонтальной. Длина нити (высота падения) определяется по шкале, нанесенной на вертикальной стойке.

Параметры установки: радиус оси 5 мм, радиус нити 0,6 мм,

радиус диска R1 = 42,5 мм,

внешний радиус кольца R2 = 52,5 мм.

Значения остальных параметров указаны на элементах маятника.

Задания и порядок их выполнения

Задание 1. Экспериментальное определение момента инерции маятника Максвелла (стандартный опыт).

Провести измерение времени падения маятника не менее 10 раз. Вычислить среднее время падения, а по нему при помощи формулы (3.8) момент инерции. Провести стандартную обработку результатов измерений. Погрешность измерения высоты принять равной θ h = 2 мм, погрешность измерения времени θ t = 0,001 c.

Внимание! При проведении опыта нужно следить за тем, чтобы нить наматывалась на ось аккуратно в один слой. Опыты, в которых это условие не соблюдается, в дальнейшем не учитывать.

Описанная выше процедура является стандартным опытом в данной работе. Ее нужно провести для маятника с каждым из сменных колец и без кольца.

Задание 2. Исследование зависимости момента инерции маятника Максвелла от высоты, с которой происходит его падение.

Для указанного преподавателем кольца провести стандартный опыт для трех разных высот h. Экспериментально убедиться в том, что момент инерции маятника не зависит от начальной высоты, и в отчете объяснить, почему. Получить среднее значение момента инерции маятника по результатам трех серий, проведенных при разных высотах.

При проведении математической обработки результатов измерений в первом и втором заданиях нужно исходить из того, что момент инерции является неслучайной величиной.

41

Задание 3. Теоретический расчет момента инерции маятника Максвелла.

По формулам (3.10), (3.11) вычислить моменты инерции диска, колец и маятника в целом во всех случаях. Сравнить расчетные значения с измеренными и объяснить расхождения, если они возникнут.

Контрольные вопросы

1.Что называется моментом инерции абсолютно твердого тела?

2.Чему равны моменты инерции диска и кольца?

3.Чему равна кинетическая энергия абсолютно твердого тела?

4.Запишите закон сохранения энергии для маятника Максвелла.

5.Является ли падение маятника равноускоренным?

6.Почему опустившись до нижней точки маятник снова начинает подниматься наверх?

7.Какая энергия маятника больше – кинетическая поступательного движения или кинетическая вращения? (При ответе на этот вопрос воспользоваться полученным значением момента инерции маятника и известным значением радиуса оси маятника.)

8.Как зависит время падения маятника Максвелла от его массы?

9.Почему падения маятника с кольцом быстрее, чем без кольца?

10.Как изменится время падения, если маятник выполнить из менее плотного чем сталь материала (например, алюминия)?

ЛАБОРАТОРНАЯ РАБОТА № 4

Математический и оборотный маятники

Цель работы: определение ускорения свободного падения, определение приведенной длины и момента инерции физического маятника.

Теоретические сведения

Физическим маятником называется абсолютно твердое тело, закрепленное на неподвижной горизонтальной оси. Плоскость, проходящая через эту ось и центр тяжести, вертикальна в положении равновесия. При отклонении маятника от этого положения возникают моменты сил, стремящиеся вернуть маятник в положение равновесия.

По основному уравнению динамики вращательного движения абсолютно твердого тела сумма моментов всех сил, приложенных к телу:

42

	∑	→	→
		Mi	= I ε .	(4.1)
		i
	В этой формуле I – момент инерции			O
			→	N
	маятника относительно оси подвеса, ε
	– его угловое ускорение, а ∑	→		α
		Mi	– сум-	C
	i
	ма моментов всех сил, к этому маятни-
	ку приложенных.			mg
				α
	На рис. 4.1 изображен физический
	маятник. Ось вращения отмечена бук-
	вой О, центр тяжести буквой С. Обозна-
	→ →			Рис. 4.1. Физический маятник
	чим OC = b . К точке С приложены две
	→		→	→

силы: сила тяжести m g и сила реакции N . Поскольку сила N направ-

лена вдоль отрезка [ОС], ее момент относительно оси О равен нулю, а сумма моментов этих сил

∑	→	→ →	→ →	→	→	→	→
	Mi	= OC × m g +	OC ×	N=	OC×	m g= ×b m g .
	i					→	→ →
Подставим этот результат в (4.1) и получим: I ε							=, b × m g.

Спроектируем полученное выражение на направление оси вращения.

Iε = − mgbsin α.

Знак минус показывает, что момент силы тяжести стремится вернуть маятник в положение равновесия. Ограничимся рассмотрением лишь малых колебаний, для которых sinα = α , и учтем, что угловое ускорение есть вторая производная от угла отклонения по времени

α′′	+	mgb	α	(t )	= 0.	(4.2)
(t )		I

Получившееся уравнение аналогично дифференциальному уравнению гармонических колебаний пружинного маятника

x′′	+ ω2 x	= 0	(4.3)
(t )	(t )

43

с циклической частотой	ω =	mgb	.	(4.4)
		I

Следовательно, при малых углах отклонения от положения равновесия физический маятник совершает гармонические колебания

α(t ) = Аcos (ωt + φ0 ),

(4.5)

период которых зависит от момента инерции маятника относительно оси O, его массы и от расстояния между центром тяжести и этой осью:

T = 2π	I	.	(4.6)
	mgb

Уравнение (4.5) содержит две константы: амплитуду А и начальную фазу ϕ 0, значения которых определяются из начальных условий. Если секундомер включить в момент прохождения маятником положения равновесия, то ϕ 0 = –90°, и уравнение (4.5) перепишется в виде

α(t ) = Аsin (ωt).

(4.7)

В случае, когда физический маятник, совершающий малые колебания, представляет собой небольшое тело, подвешенное на легкой длинной нерастяжимой нити, его можно считать математическим маятником. Математическим маятником называется материальная точка, подвешенная на невесомой нерастяжимой нити, совершающая под действием силы тяжести малые колебания. Такие колебания являются гармоническими и описываются функциями (4.5) или (4.7).

Момент инерции математического маятника относительно оси, проходящей через точку подвеса, I = ml2, где l – длина нити. Подставляя это выражение в (4.4) и (4.6), найдем циклическую частоту и период колебаний математического маятника.

ω = g	l	,		(4.8)
T = 2π	l	g	.	(4.9)

Таким образом, частота и период колебаний математического маятника зависят от его длины и ускорения свободного падения. От массы маятника они не зависят.

44

Сравнивая друг с другом формулы (4.6) и (4.9), замечаем, что математический маятник с длиной нити

L =	I
		(4.10)
	mb

будет иметь такой же период колебаний, что и физический маятник. Величина, определяемая выражением (4.10), называется приведенной длиной физического маятника.

Для любого физического маятника можно указать такую пару параллельных осей, периоды малых колебаний относительно которых одина-

ковы, а расстояние между ними равно
приведенной длине физического маят-
ника.	A	C	B
Докажем это утверждение. На рис.	a		b

4.2 изображен физический маятник, который может быть подвешен на од-

	ной из двух параллельных осей А или	Рис. 4.2. Физический
		маятник
	В. Центр тяжести маятника обозначим
	точкой С. Введем обозначения a и b,
	смысл которых понятен из рисунка:

AC = a; BC = b.

Моменты инерции маятника относительно осей А, В и относительно оси, проходящей через точку С параллельно осям А и В, обозначим соответственно IA, IВ, IС. По теореме Штейнера значения этих величин связаны друг с другом соотношением: IA = IС + ma2; IВ = IС + mb2.

Периоды малых колебаний маятника относительно этих осей:

IC

+ ma2

IC + mb2

TA

= 2π

; TB = 2π

.

(4.11)

mga

mgb

Если положения осей А и В выбраны так, что периоды одинаковы, то

IC

+ ma2

=

IC

+ mb2

, откуда следует, что

IC = mab.

(4.12)

a

b

Подставляя (4.12) в любую из формул (4.11), получаем

T

=

T =

mab + ma

2

= 2π

a + b

A

.

(4.13)

B

mga

g

45

Величина a + b есть расстояние между осями подвеса, но она же, согласно определению, есть приведенная длина физического маятника.

Доказанное свойство демонстрирует оборотный маятник. Оборотным называется физический маятник с двумя параллельными призмами, на любой из которых он может быть подвешен. Перемещением опорных призм можно добиться того, что периоды колебаний маятника на любой из них окажутся одинаковыми. Расстояние между призмами при этом окажется равным приведенной длине. Измерив его и зная период колебаний маятника, можно найти ускорение свободного падания g:

g =	4π2 L	.	(4.14)
	T 2

Определив положение центра тяжести оборотного маятника и измерив расстояния от этой точки до каждой из призм, т. е. расстояния a и b, по формуле (4.12) можно найти момент инерции маятника Ic.

Лабораторная установка

		5
5
6		6
7		7
	9
	8
10	4	11
11	3
	2
	1
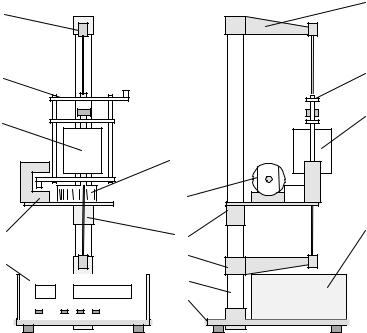
Рис. 4.3.	Внешний вид лабораторной установки

46

Внешний вид установки приведен на рис. 4.3. Установка состоит из математического и оборотного маятников. Математический маятник выполнен в виде металлического шарика 1 на бифилярном подвесе 2. Длина подвеса измеряется линейкой на стойке 3.

Оборотный маятник состоит из металлического стержня 4, на котором крепятся две подвижные опорные призмы 5 и два груза 6, перемещение которых изменяет распределение масс. Фотодатчик 7 на нижнем кронштейне сигнализирует о прохождении маятником положения равновесия. Время измеряется миллисекундомером, а число колебаний специальным счетчиком. Прибор включается нажатием кнопки "Сеть". Кнопка "Сброс" служит для установки нуля. Нажатие кнопки "Стоп" выключает прибор после окончания текущего колебания.

Для упрощения измерения расстояния на стержне через каждый сантиметр нанесены риски. Размеры и массы элементов оборотного маятника показаны на рис. 4.7.

Задания и порядок их выполнения

Задание 1. Определение ускорения свободного падения при помощи математического маятника.

Верхнюю планку следует развернуть таким образом, чтобы математический маятник оказался над фотодатчиком, и в положении равновесия он пересекал оптическую ось.

Перед началом измерений нажимают кнопку "Сброс". Шарик отклоняют на небольшой угол ~4–5° и осторожно без толчка отпускают. Когда на счетчике колебаний появляется цифра 9, нажимают кнопку "Стоп". В таком случае прибор измерит время десяти полных колебаний и найти их средний период будет очень просто. Определение периода колебаний проводится таким методом не менее пяти раз при различных длинах маятника L. Для каждого значения периода и соответствующей длины при помощи формулы (4.14) находится ускорение свободного падения. Необходимо провести стандартную математическую обработку результатов измерения g.

Задание 2. Определение ускорения свободного падения при помощи оборотного маятника.

Верхнюю планку повернуть так, чтобы нижняя часть оси оборотного маятника проходила через прорезь фотодатчика. Грузы на стержне лучше фиксировать несимметрично, чтобы один находился у конца стерж-

47

	A		ня, другой – около его середины. При-
			змы следует закрепить по разные сторо-
			ны от центра тяжести маятника. Одну при-
			змуследуетпоместитьближексвободному
			концу стержня, другую – между грузами.
l			Сначаламаятникследуетподвеситьнапри-
			зме А, которая ближе к его концу, как это
			показано на рис. 4.4. Отклонить маятник
			на небольшой угол ~ 4–5° и осторожно без
			толчка отпустить его. Нажать кнопку
	B		"Сброс"; включится секундомер и счетчик
			колебаний.Когданасчетчикеколебанийпо-
			явится цифра 9, нажать кнопку "Стоп". В
			таком случае прибор измерит время десяти
			полных колебаний и найти их средний пе-
			риод Т0 будет очень просто.
			После измерения Т0 нужно снять ма-
			ятник, измерить расстояние l между при-
Рис. 4.4. Положение маятника			змами, перевернуть его и подвесить на
при измерении периода Т1			призме В. Нижний кронштейн с фотодат-
			чиком поднять так, чтобы маятник пере-
секал оптическую ось. По десяти колебаниям определить среднее зна-
чение периода Т1. Если окажется, что Т1 > Т0, то вторую призму
переместить,	чтобы	расстояние		l	увеличилось;	если
Т1 < Т0, то чтобы уменьшилось. Перемещать призму следует на целое
число делений, поскольку в этом случае она закрепляется наиболее на-
дежно. Положение первой призмы и грузов изменять нельзя. Измерить
новый период колебаний Т2 и снова сравнить его с Т0. Призму В следует
перемещать, пока не окажется, что периоды колебаний ТK–1 и ТK при
соседних положениях призмы окажутся чуть меньше и чуть больше чем
Т0. По двум соответствующим длинам lк				и lк–1 найти приведенную дли-
ну L и ее систематическую погрешность				θ L.
В простейшем случае для вычисления длины можно воспользовать-
ся формулой

L = 0,5(lk + lk −1).

(4.15)

Систематическая погрешность приведенной длины оборотного маятника при этом равна половине цены деления, т. е. θ L = 0,5 см.

48

Рис. 4.5. Определение приведенной длины маятника

lk

lk – 1

L

Tk

k

Tk–1

T0

k –

1

T

По заданию преподавателя студенту может быть предложе-

но получить приведенную длину более точным методом. На рис. 4.5 показан участок зависимости периода колебаний Т от

расстояния между призмами l; на нем отмечены два последних из-

мерения под номерами k – 1, и k, а также период Т0. Из этого рисунка видно, как графически находится приведенная длина обо-

ротного маятника. Для обозначенных величин справедлива пропорция

lk − L = T0 − Tk . lk − lk −1 Tk −1 − Tk

Перепишем ее, введя обозначения ∆ T = Tk–1 – Tk и ∆ l = lk – lk–1 = 1 см.

L = l	−	∆l	(T	− T	).	(4.16)
k		∆T	0	k

Систематическую погрешность определения приведенной длины этим методом можно принять θ L = 2 мм.

Зная приведенную длину и период, по формуле (4.14) следует найти ускорение свободного падения g. На основании погрешности θ L нужно оценить систематическую погрешность θ g.

Случайную погрешность в первом и втором заданиях определять не имеет смысла, поскольку различия измеренных периодов обусловлены не столько случайными ошибками измерений, сколько слабой зависимостью периода колебаний от амплитуды. Систематическую погрешность измерения периода принять равной θ T = 0,005 с.

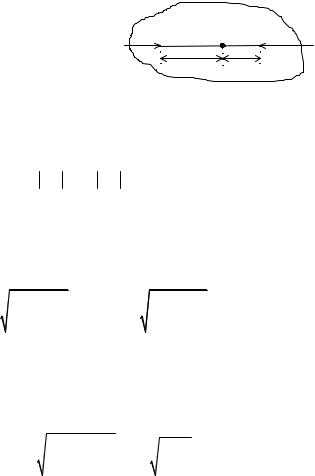
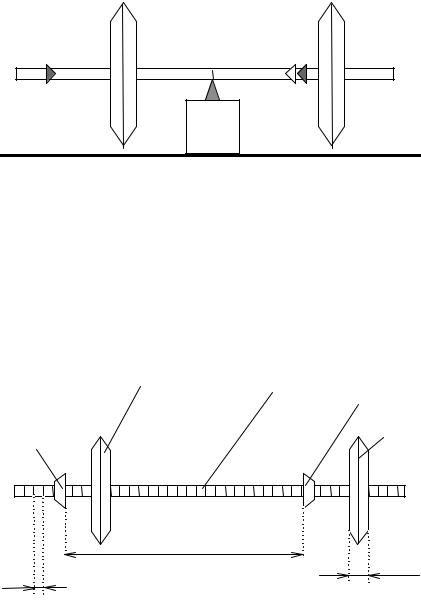
Задание 3. Определение момента инерции оборотного маятника. Не меняя положения призм А и В после выполнения задания 2 най-

ти положение центра тяжести маятника. Для этого снять маятник, развернуть его горизонтально и положить на острие, как это показано на рис. 4.6. На нем указаны два последних положения призмы В.

49

A C B

Рис. 4.6. Определение центра тяжести оборотного маятника

Нужно измерить расстояние a между точками А и В. Расстояние b между точками B и C лучше не измерять, а вычислить b = L – a, поскольку положение точки В находится, строго говоря, между двумя последними положениями призмы с порядковыми номерами k – 1 и k.

Массу маятника вычислить по величинам, указанным на рис. 4.7. По формуле (4.12) вычислить момент инерции маятника. Оценить систематическую погрешность θ I.

1130 г	350 г

15 г

1130 г

15 г

L

2 см

1 см

Рис. 4.7. Размеры и массы элементов оборотного маятника

50