
- •Министерство образования и науки российской федерации
- •Введение
- •Методические указания, примеры выполнения заданий задание 1
- •Решение системы методом определителей.
- •Решение систем матричным методом.
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 10
- •Задание 11
- •Учебное Пособие для выполнения контрольной работы № 1 по математике
- •394036 Воронеж, пр. Революции, 19.
Решение систем матричным методом.
Квадратной матрицей 3-го порядка называется таблица из 3-х строчек и 3-х столбцов.
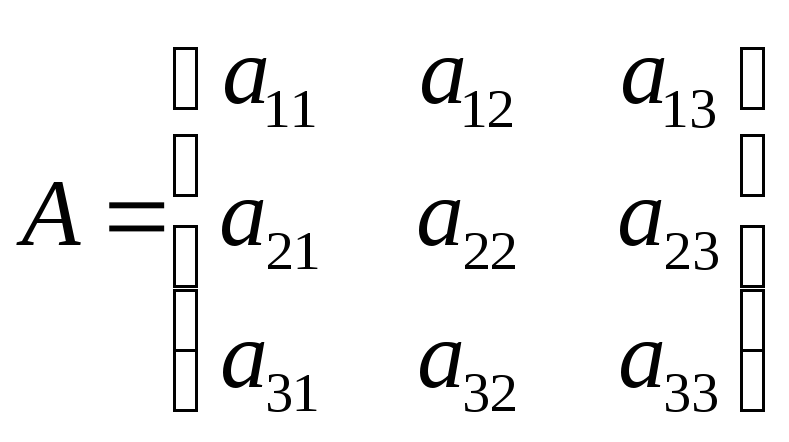 .
(7)
.
(7)
Внешне
матрица
![]() похожа на определитель 3-го порядка, но
определитель 3-го порядка - число, которое
находится по формуле (1), а матрица
похожа на определитель 3-го порядка, но
определитель 3-го порядка - число, которое
находится по формуле (1), а матрица![]() - набор информации из девяти чисел,
расположенных в виде (7). При написании
они отличаются тем, что определитель
по бокам имеет прямые линии, а матрица
– скобки. Элементы матрицы
- набор информации из девяти чисел,
расположенных в виде (7). При написании
они отличаются тем, что определитель
по бокам имеет прямые линии, а матрица
– скобки. Элементы матрицы![]() и определителя
и определителя![]() называются одинаково: строки, столбцы,
главная и побочная диагонали.
называются одинаково: строки, столбцы,
главная и побочная диагонали.
Введем определение единичной матрицы:
 .
(8)
.
(8)
У
единичной матрицы
![]() на главной диагонали элементы равны 1,
а все остальные элементы равны 0.
на главной диагонали элементы равны 1,
а все остальные элементы равны 0.
Матрицы
можно транспонировать, т.е. из
![]() образовать новую матрицу
образовать новую матрицу![]() ,которая
получается из
,которая
получается из![]() путем замены строк соответствующими
столбцами.
путем замены строк соответствующими
столбцами.
 .
(9)
.
(9)
Две
матрицы
![]() и
и![]() можно перемножать, в результате получим
новую матрицу
можно перемножать, в результате получим
новую матрицу![]() :
:
![]() ;
;
 .
(10)
.
(10)
Элементы
матрицы
![]() находятся по правилу: если индексы
находятся по правилу: если индексы![]() и
и![]() то
элемент
то
элемент![]() равен сумме произведений элементов на
равен сумме произведений элементов на![]() -й
строке матрицы
-й
строке матрицы![]() на соответствующие элементы на
на соответствующие элементы на![]() -ом
столбце матрицы
-ом
столбце матрицы![]() .
.
Пример:
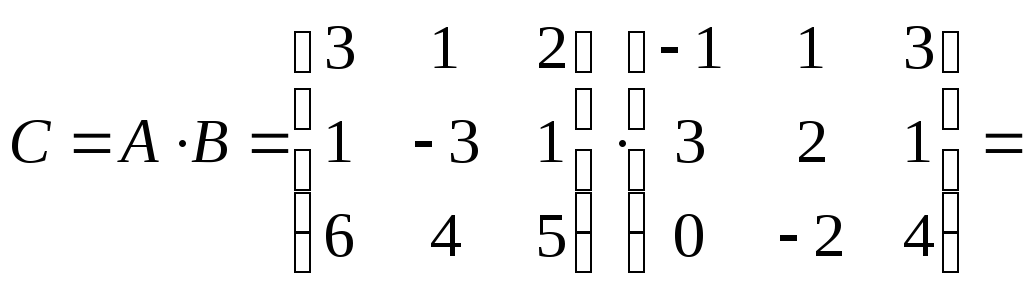
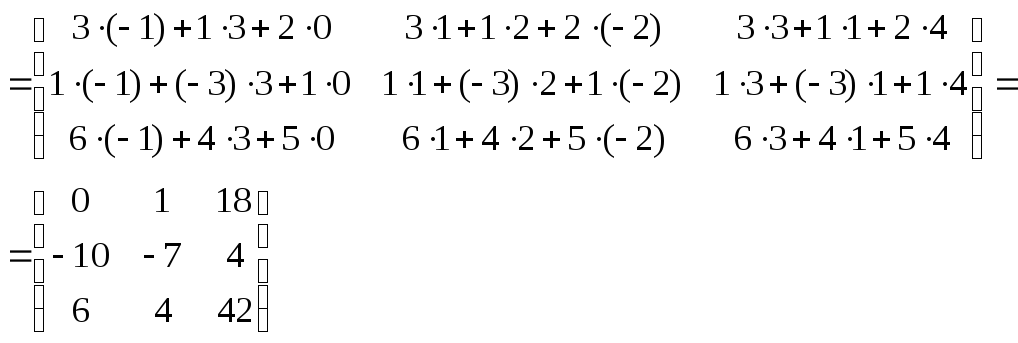
Далее
понадобится понятие вектор – столбца.
Обычно проекции вектора располагают
строчкой
![]() .
Если эти же проекции расположить
вертикально, то получим вектор – столбец:
.
Если эти же проекции расположить
вертикально, то получим вектор – столбец:
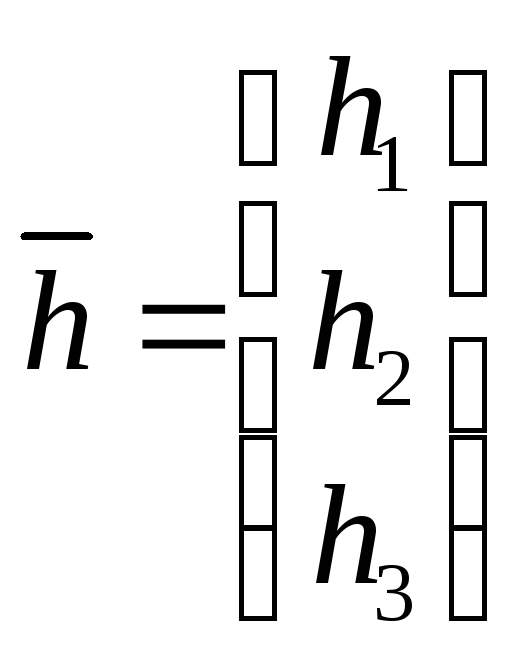 .
(11)
.
(11)
Подобный
вектор – столбец используется в
произведении с матрицей. Произведением
матрицы
![]() на вектор – столбец
на вектор – столбец![]() называется новый вектор
называется новый вектор![]() элементы которого равны сумме произведений
соответствующей строки матрицы
элементы которого равны сумме произведений
соответствующей строки матрицы![]() на элементы вектора – столбца
на элементы вектора – столбца![]() ,
т. е.
,
т. е.
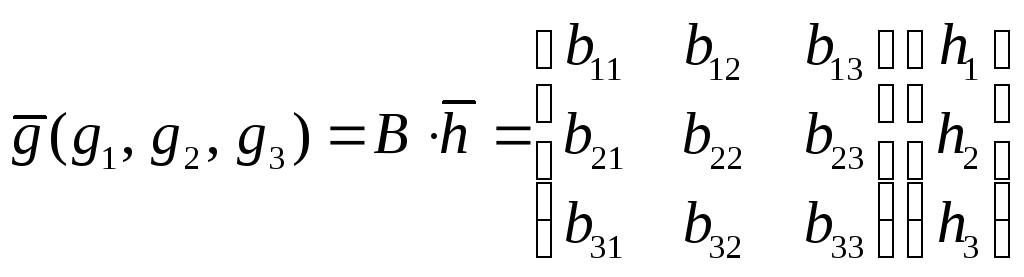 ,
(12)
,
(12)
где
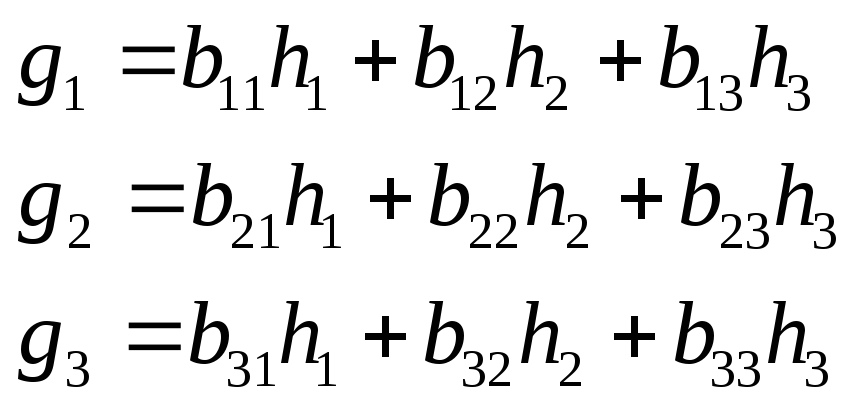 .
(13)
.
(13)
Еще необходимо определить обратную матрицу.
Матрица
![]() называется обратной матрицей к матрице
называется обратной матрицей к матрице![]() ,
если имеют место следующие матричные
равенства:
,
если имеют место следующие матричные
равенства:
![]() .
(14)
.
(14)
Для
всякой матрицы
![]() ,
если ее определитель
,
если ее определитель![]() ,
существует обратная матрица. Обратная
матрица
,
существует обратная матрица. Обратная
матрица![]() строится следующим образом:
строится следующим образом:
1.
Вычисляем определитель
![]() данной матрицы
данной матрицы![]() .
.
2.
Для элементов
![]() матрицы
матрицы![]() вычисляем алгебраические дополнения
вычисляем алгебраические дополнения![]() по
правилу:
по
правилу:![]() равно определителю второго порядка
взятого со знаком
равно определителю второго порядка
взятого со знаком![]() и получаемого вычеркиванием
и получаемого вычеркиванием![]() -й
строки и
-й
строки и![]() -го
столбца из определителя
-го
столбца из определителя![]() .
.
Например:
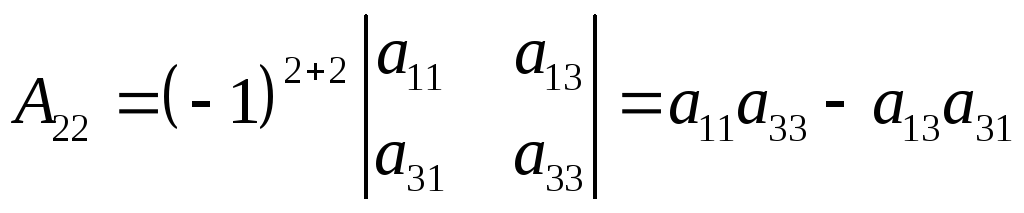

3.
Из элементов
![]() составляем
матрицу
составляем
матрицу![]() .
.
 .
(15)
.
(15)
4.
Каждый элемент матрицы
![]() делим на определитель
делим на определитель![]() и транспонируем полученную матрицу. В
результате находим обратную матрицу:
и транспонируем полученную матрицу. В
результате находим обратную матрицу:
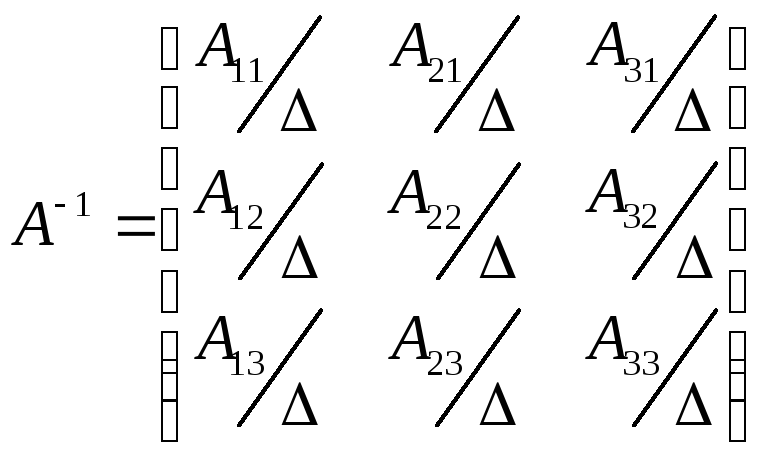 .
(16)
.
(16)
Пример вычисления обратной матрицы.
Найдем обратную матрицу для системы (6):
1.
Определитель
![]() данной матрицы уже найден
данной матрицы уже найден![]() .
Так как
.
Так как![]() ,
то обратная матрица существует.
,
то обратная матрица существует.
2.
Найдем алгебраические дополнения
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
3.
Составим матрицу
![]()
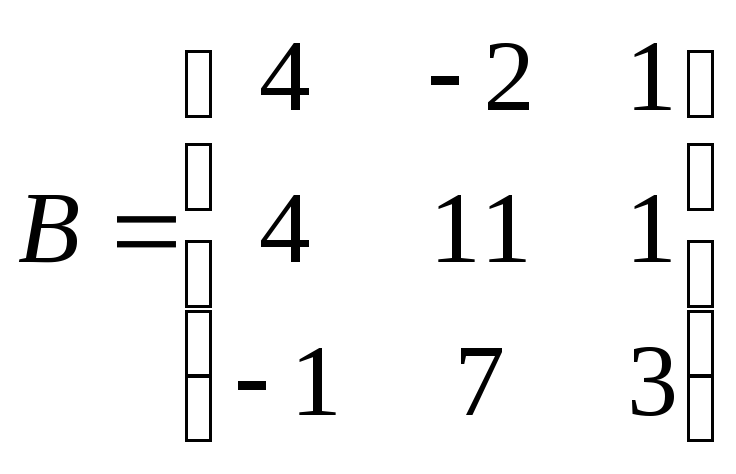
4.
Найдем обратную матрицу
![]() :
:
 .
(17)
.
(17)
Проверку сделаем по формуле (14):
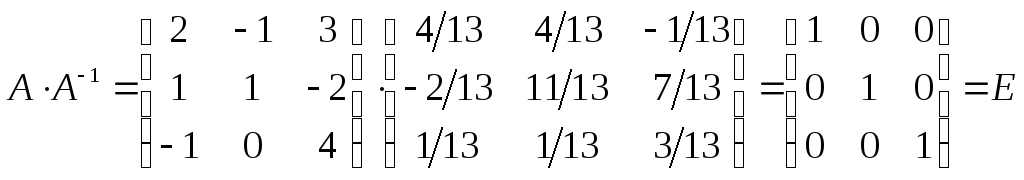 .
.
Алгебраическую систему (2) можно записать в матричной форме
![]() (18)
(18)
где
![]() – матрица из коэффициентов уравнений,
– матрица из коэффициентов уравнений,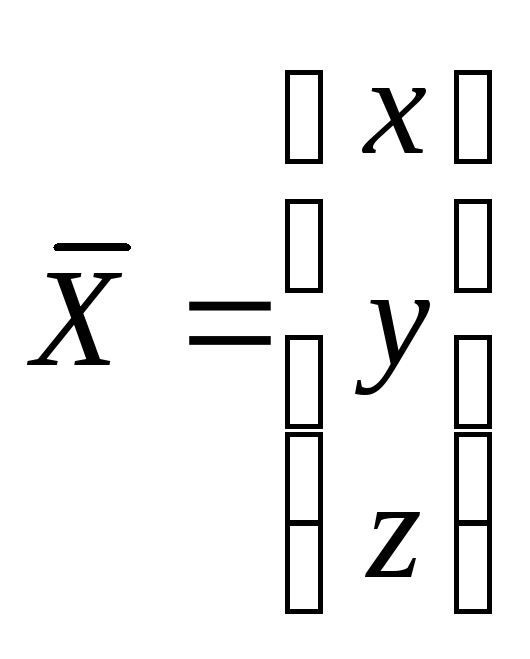 – вектор – столбец из неизвестных,
– вектор – столбец из неизвестных,![]() – вектор – столбец из правых частей
системы.
– вектор – столбец из правых частей
системы.
Если
уравнение (18) слева умножить на
![]() ,
то получим решение системы (2) в виде
,
то получим решение системы (2) в виде
![]() .
.
Пример
Решим
систему (6) матричным методом. Обратная
матрица для этой системы уже найдена
(уравнение (17)). Поэтому сразу найдем
![]() .
.

Ответ:
![]() .
.
