
- •Глава 15. Определённый интеграл
- •§15.1.Понятие площади плоской фигуры. Задача о вычислении площади криволинейной трапеции
- •15.1.1. Площадь многоугольника
- •§15.2. Определение интеграла и необходимое условие его существования
- •15.2.1Разбиение отрезка. Интегральные суммы. Определение интеграла (по Риману)
- •15.2.2.Необходимое условие интегрируемости функции
- •§15.3. Критерий интегрируемости
- •15.3.1. Определение сумм Дарбу
- •15.3.2. Свойства сумм Дарбу
- •§15.4. Критерий интегрируемости функции. Классы интегрируемых функций
- •15.4.1. Критерий интегрируемости функции
- •15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции
- •§15.5. Свойства определённого интеграла
- •Тогда объединение разбиений иобразует некоторое размеченное разбиениеотрезкас, для которого справедлива формула. Поэтому, с учетом неравенств (18)(20), имеем оценки
- •§15.6. Теоремы о среднем значении
- •§15.7. Определённый интеграл с переменным верхним пределом
- •§15.8. Основная формула интегрального исчисления (Формула Ньютона-Лейбница)
- •15.8.1. Основная формула интегрального исчисления
- •15.8.2. Замена переменной и интегрирование по частям в определённом интеграле.
15.4.2. Интегрируемость монотонной функции. Интегрируемость непрерывной функции
Следствием доказанного критерия 15.5.является интегрируемость монотонной функции.
Теорема 15.6.
Если
![]() не убывает (не возрастает) на
не убывает (не возрастает) на![]() ,
то она интегрируема на
,
то она интегрируема на![]() .
.
► Пусть
![]() не убывает. Тогда на отрезке
не убывает. Тогда на отрезке![]() выполняются
выполняются
равенства:
![]() ,
,![]() .
Если
.
Если![]() ,
то
,
то![]() - постоянная и ее
- постоянная и ее
интегрируемость
очевидна (![]() ).
Если
).
Если![]() ,
то положим
,
то положим
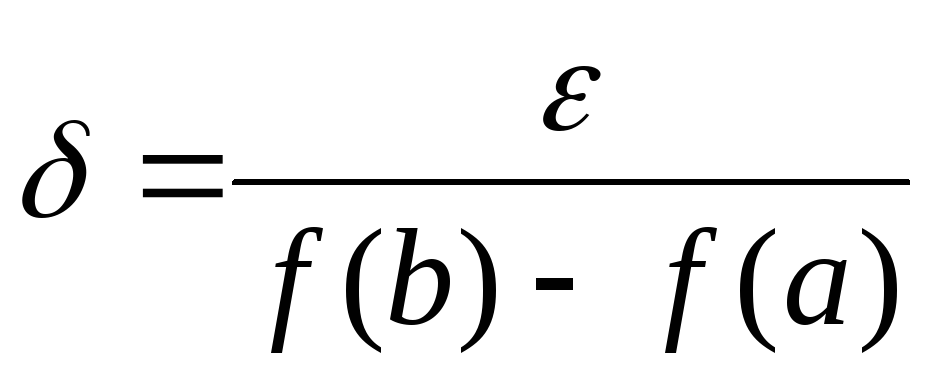 .
.
Тогда если
![]() ,
то
,
то![]()
◄
Докажем теорему, которая будет очень часто использоваться.
Теорема 15.7.
. Если
![]() ,
то
,
то
![]() — интегрируема на
— интегрируема на
![]() .
.
► По теореме
Кантора,
![]() равномерно непрерывна на
равномерно непрерывна на
![]() ,
т.е.
,
т.е.
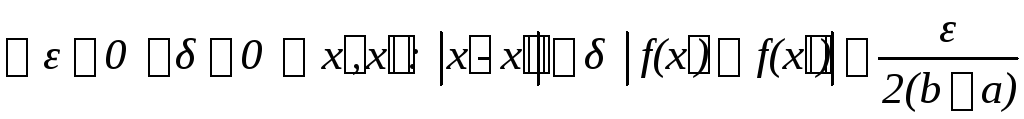 (10).
(10).
Рассмотрим разбиение
![]() отрезка
отрезка
![]() с диаметром меньшим, чем выбранное
с диаметром меньшим, чем выбранное
![]() .
Тогда на каждом отрезке
.
Тогда на каждом отрезке
![]() имеет место неравенство:
имеет место неравенство:
![]() (11).
(11).
Действительно,
достаточно подобрать точку
![]() так, что
так, что
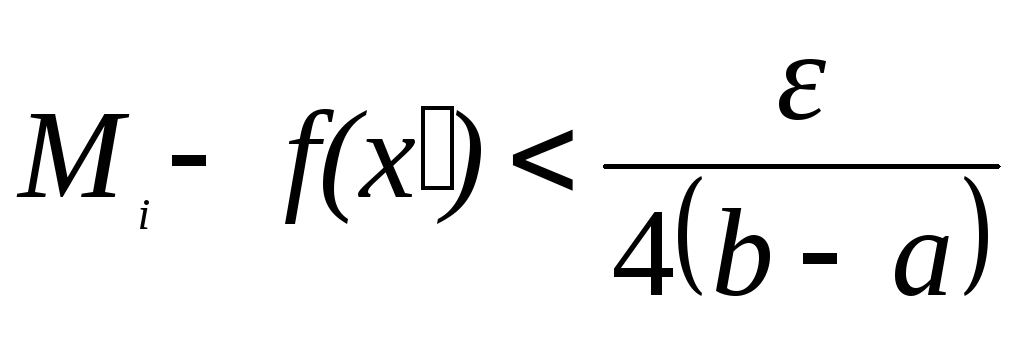 (12)
(12)
и точку
![]() так, чтобы
так, чтобы
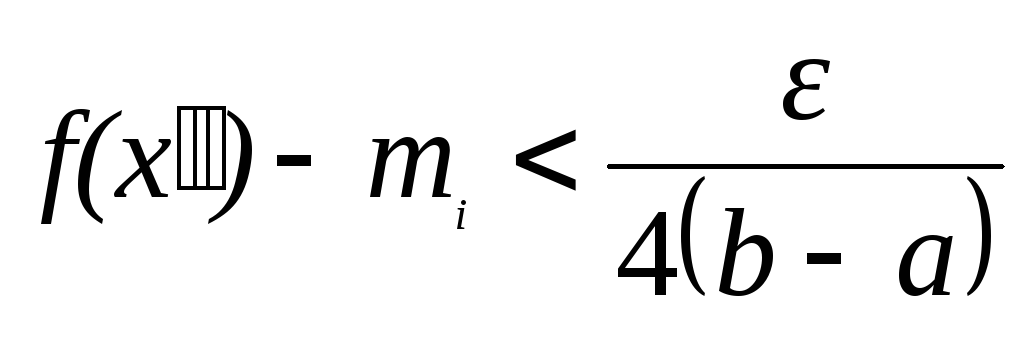 (13).
(13).
(Это можно сделать,
т.к. числа
![]() — точные грани множества значений).
— точные грани множества значений).
Тогда ввиду (10),
(12),
(13)
![]() ,
и
,
и
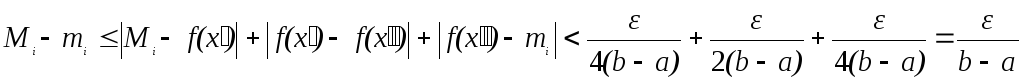 .
Неравенство (11)
доказано. Тогда
.
Неравенство (11)
доказано. Тогда
![]() .
.
То есть критерий интегрируемости выполняется.◄
Ещё раз вернёмся к задаче о площади криволинейной трапеции.
Теорема 15.8.
Пусть
![]() — фигура, ограниченная снизу осью
— фигура, ограниченная снизу осью![]() ,
по бокам — отрезками вертикальных
прямых
,
по бокам — отрезками вертикальных
прямых![]() и
и![]() ,
,![]() ,
а сверху — графиком непрерывной на
отрезке
,
а сверху — графиком непрерывной на
отрезке![]() функции
функции![]() (см. рис.1). Тогда
(см. рис.1). Тогда![]() имеет площадь, причем
имеет площадь, причем
![]() =
=
![]()

Рис. 1. Рис. 2.
►Для произвольного
разбиения
![]() отрезка
отрезка![]() нижняя сумма Дарбу
нижняя сумма Дарбу![]() представляет собой площадь многоугольника
представляет собой площадь многоугольника![]() ,
,![]() ,
а верхняя сумма Дарбу — площадь
многоугольника
,
а верхняя сумма Дарбу — площадь
многоугольника![]() ,
,![]() (рис. 2). Так как
(рис. 2). Так как![]() непрерывна на
непрерывна на![]() ,
она интегрируема на этом отрезке и для
любого
,
она интегрируема на этом отрезке и для
любого![]() существует
существует![]() такое, что для всех разбиений
такое, что для всех разбиений![]() с диаметром
с диаметром![]() имеет место неравенство
имеет место неравенство![]() .
Значит, для любого
.
Значит, для любого![]() существуют многоугольники
существуют многоугольники![]() такие, что
такие, что![]() .
Это означает квадрируемость
.
Это означает квадрируемость
![]() .
Наконец, площадь
.
Наконец, площадь![]() равна
равна![]() и
и ![]() .
Эти равенства означают, что
.
Эти равенства означают, что
![]() .◄
.◄
Следствие.
Пусть
![]() и
и![]() — непрерывные на
— непрерывные на![]() функции, причем для всех
функции, причем для всех![]() выполняется неравенство
выполняется неравенство![]() .
Тогда площадь криволинейной трапеции,
ограниченной сверху графиком функции
.
Тогда площадь криволинейной трапеции,
ограниченной сверху графиком функции![]() ,
снизу — графиком функции
,
снизу — графиком функции![]() ,
а по бокам — отрезками вертикальных
прямых
,
а по бокам — отрезками вертикальных
прямых![]() и
и![]() равна
равна
![]() .
.
►Так как интегрируемые
функции ограничены, существует постоянная
![]() такая, что
такая, что![]()
![]() .
Площадь между графиками функций
.
Площадь между графиками функций
![]() и
и![]() такая же, как площадь между графиками
функций
такая же, как площадь между графиками
функций![]()
![]() .
Для доказательства следствия достаточно
применить к этим функциям теорему 15.8,
заметить, что искомая площадь равна
разности площадей
.
Для доказательства следствия достаточно
применить к этим функциям теорему 15.8,
заметить, что искомая площадь равна
разности площадей
![]()
и применить теорему 15.13 из следующего параграфа, согласно которой
![]()
![]() ◄
◄
Теорема 15.9 . Если
функция
![]() ограничена на отрезке
ограничена на отрезке![]() и имеет на нем конечное число точек
разрыва, то она интегрируема на этом
отрезке.
и имеет на нем конечное число точек
разрыва, то она интегрируема на этом
отрезке.
►Ограничимся схемой доказательства.
Для любого разбиения
![]() отрезка
отрезка![]() полученные отрезки
полученные отрезки![]() либо содержат точку разрыва, либо не
содержат. Количество отрезков, куда
может входить точка разрыва, не превосходит
удвоенного числа точек разрыва, так как
точка разрыва может принадлежать одному
отрезку (когда она не совпадает с точкой
деления), либо двум отрезкам (когда она
совпадает с точкой деления). По условию,
функция
либо содержат точку разрыва, либо не
содержат. Количество отрезков, куда
может входить точка разрыва, не превосходит
удвоенного числа точек разрыва, так как
точка разрыва может принадлежать одному
отрезку (когда она не совпадает с точкой
деления), либо двум отрезкам (когда она
совпадает с точкой деления). По условию,
функция
![]() ограничена, поэтому существуют точная
нижняя грань
ограничена, поэтому существуют точная
нижняя грань![]() и точная верхняя грань
и точная верхняя грань![]() множества её значений. Следовательно,
колебание
множества её значений. Следовательно,
колебание![]() на любом отрезке, содержащем точку
разрыва, не превосходит
на любом отрезке, содержащем точку
разрыва, не превосходит![]() .
.
Таким образом, для
любого
![]() можно выбрать
можно выбрать![]() столь малым, чтобы сумма величин
столь малым, чтобы сумма величин![]() для отрезков, содержащих точки разрыва,
стала меньше
для отрезков, содержащих точки разрыва,
стала меньше![]() .
.
Так же, как при
доказательстве теоремы об интегрируемости
непрерывной функции, можно доказать,
что сумма величин
![]() для отрезков, не содержащих точек
разрыва, меньше, чем
для отрезков, не содержащих точек
разрыва, меньше, чем![]() ,
при достаточно малых значениях
,
при достаточно малых значениях![]() .
.
Но это означает,
что при достаточно малых
![]() вся сумма
вся сумма
![]() и теорема
доказана.◄
и теорема
доказана.◄
