13.1.4. Пример отыскания условного экстремума

Решим задачу:

Найти экстремумы функции при условии .

Дадим два решения этой задачи.

Первое решение основано на том, что уравнение связи можно в явном виде решить: и получить, подставив эти значения в функцию , соответственно, две непрерывные функции от : , .

Для решения поставленной задачи следует найти экстремумы этих функций. Первая из них имеет максимум в точке , вторая – минимум в точке .(Проверьте это самостоятельно).

Недостатком предложенного выше способа является то, что мы использовали явный вид решения уравнения связи. Во многих случаях решить уравнения связи непросто. Поэтому рассмотрим второе решение, которое использует изложенный выше метод Лагранжа.

Строим функцию Лагранжа . Составим и решим соответствующую систему уравнений

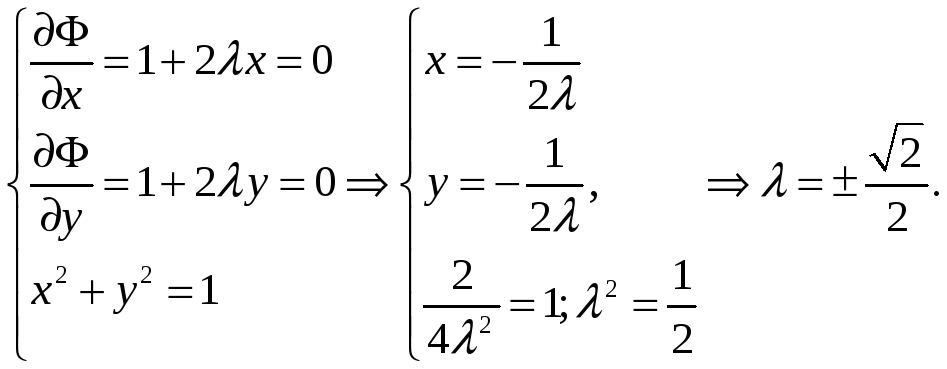
При получаем При

Функция может иметь условный экстремум только в этих точках.

Выясним, действительно ли в этих точках есть экстремумы.

С этой целью найдем .

Вторые частные производные равны .

Из условия следует , и в точк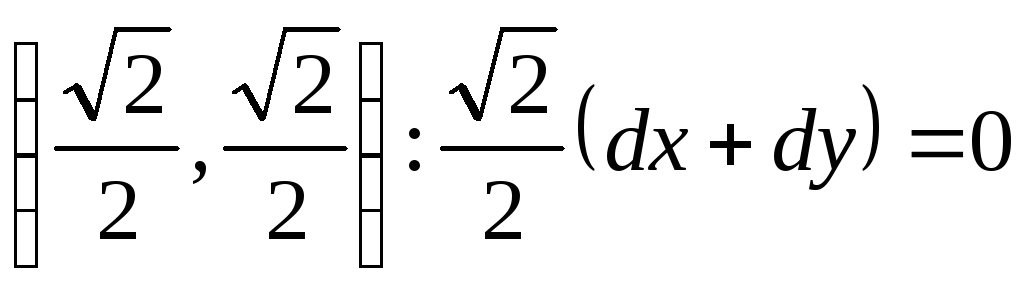е , т.е. . В точке , т.е. снова . Поэтому .

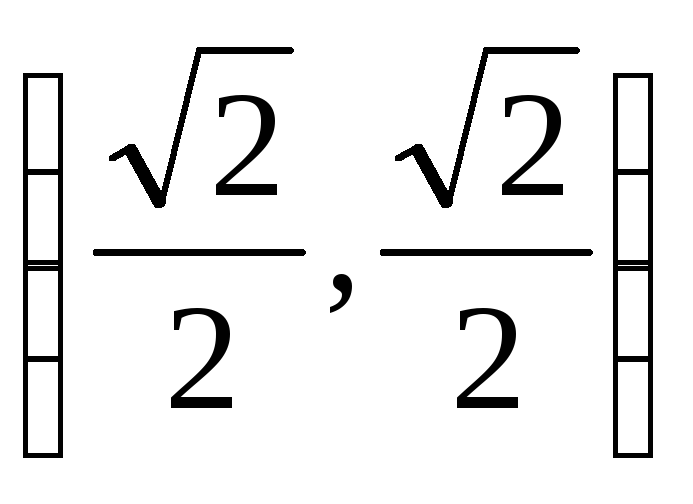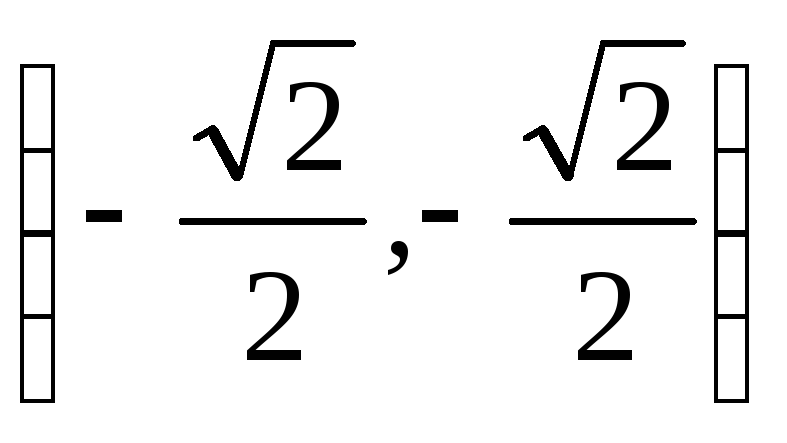В точке второй дифференциал равен , т.е. в этой точке имеем условный максимум, а в точке – второй дифференциал равен , т.е. в этой точке имеем условный минимум.

Для иллюстрации теории, описанной в предыдущем пункте, рассмотрим окаймлённый гессиан

,

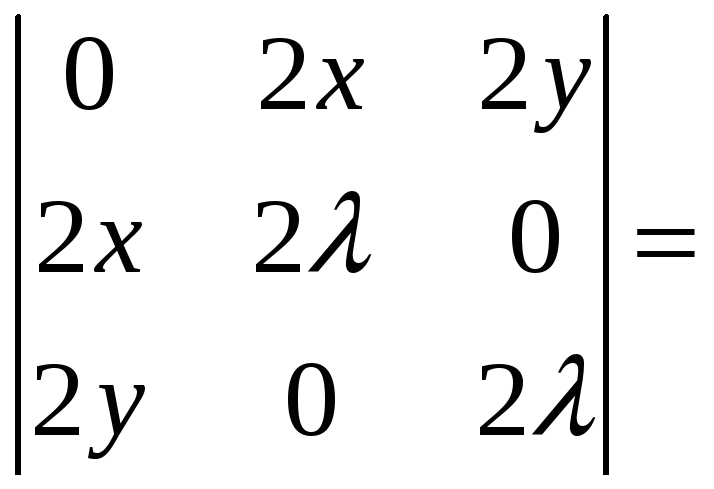
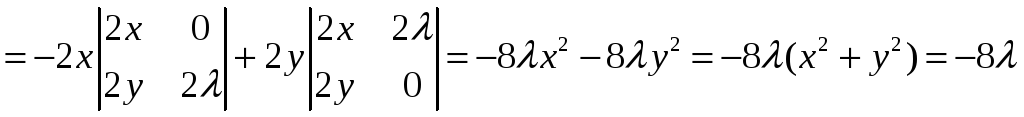последнее равенство получено, как следствие уравнения связи. При в соответствующей точке имеем минимум, так как окаймлённый гессиан отрицателен( равен ). При в точке имеем максимум, так как окаймлённый гессиан положителен( равен ).

§ 13.2.Приложения теории условного экстремума к экономической теории

13.2.1. Задача рационального поведения потребителя на рынке. Функции спроса по Маршаллу. Функция косвенной полезности

Постановка задачи. Требуется купить два товара, один – стоимостью за единицу, другой – стоимостью за единицу измерения (предполагается, что можно купить любые количества этих товаров). Наличные средства обозначим . Товары в количестве обладают совокупной полезностью .

Следует добиться наибольшего значения функции полезности при

условии, что расходы не превосходят .

Предварительные замечания. Задача сводится к нахождению

наибольшего значения функции на области , ограниченной

прямыми и .

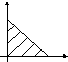
В большинстве реальных задач рассматриваемая функция полезности такова, что наибольшее значение эта функция полезности принимает именно на границе .

Однако рассмотрим общий случай сформулированной задачи для произвольной дифференцируемой функции .

Сначала ищем экстремум во внутренних точках области, решая систему

и исследуя найденные точки, используя достаточный признак экстремума.

Затем рассмотрим функцию на отрезке и посчитаем её наибольшее значение; то же для функции на отрезке .

Осталось найти наибольшее значение функции при условии , после чего, сравнивая вышеупомянутые наибольшие значения внутри области и на её границах, получим решение задачи.

Отметим, что эта процедура пригодна для произвольной дифференцируемой функции .

Приступим к задаче о нахождении условного экстремума функции

при условии

(10)

Для этого построим функцию Лагранжа

(11)

и приравняем к нулю её частные производные

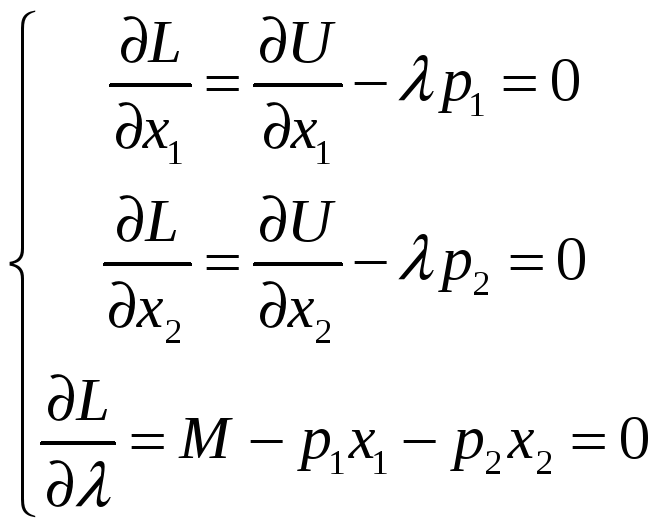(12)

Пусть система (12) имеет единственное решение, которое обозначим (13)

Функции называются функциями спроса по Маршаллу. Функция

(14)

называется функцией косвенной полезности.

Поскольку являются решениями системы (12), имеют место равенства

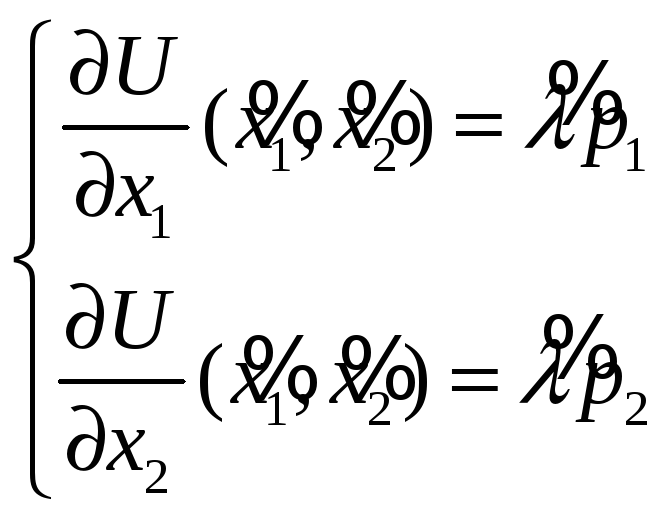или , (15)

При равенство (10) принимает вид

(16)

Считаем, что - дифференцируемые функции и, дифференцируя это равенство по , находим:

. (17)

Предположим, что – переменная величина, и не зависят от . Тогда, дифференцируя (16) по , находим

,

откуда

(18)

и, аналогично,

. (19)

Утверждение. Имеет место равенство

. (20)

► Из (14),(15) и (17) следует, что

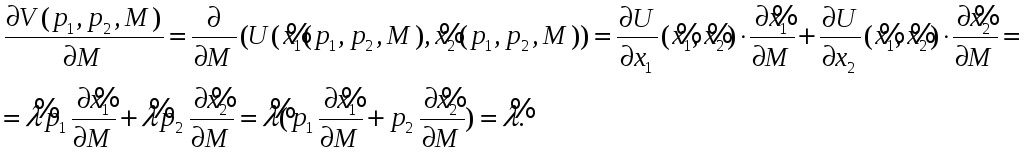
Равенство (20) доказано.◄

Утверждение (тождество Роя). Имеют место равенства

, (21)

► Из (14),(15),(18),(19) получаем

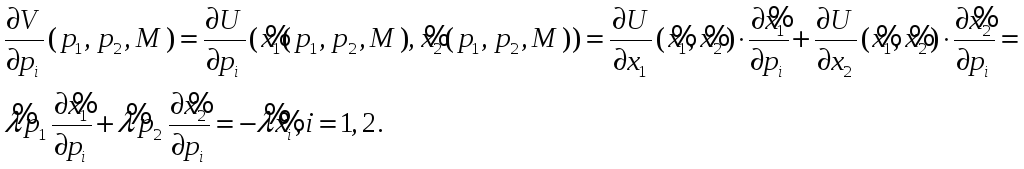
Тождества (21) доказаны.◄

Пример. Рассмотрим функцию полезности вида

, . (22)

Функция Лагранжа (11) , согласно (22) и (10), принимает вид

. (23)

Её производные, приравненные к нулю, дают систему уравнений

(24)

Из третьего уравнения системы находим

. (25)

Подставляя это значение в первые два уравнения системы (24), получаем

,

или

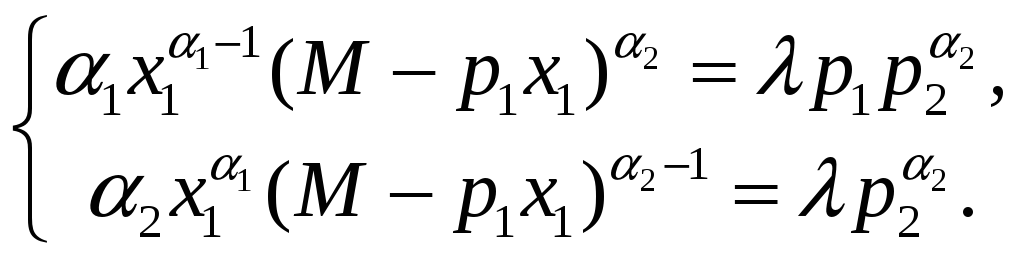(26)

Разделим первое из уравнений (26) на второе и найдём:

,

откуда

. (27)

Из (25) и (27) находим:

. (28)

Напомним, что по определению решения (27) и (28) системы (24) называются функциями спроса по Маршаллу(13) и обозначаются . Таким образом,

.

Отметим, что в примере зависит от , и не зависит от , а зависит от , но не зависит от .

Функция косвенной полезности (14) равна

.

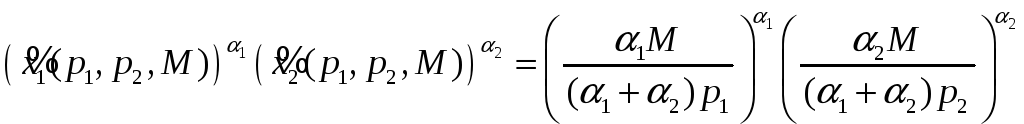Наконец, соответствующее значение находим, подставляя в любое из уравнений (26):

,

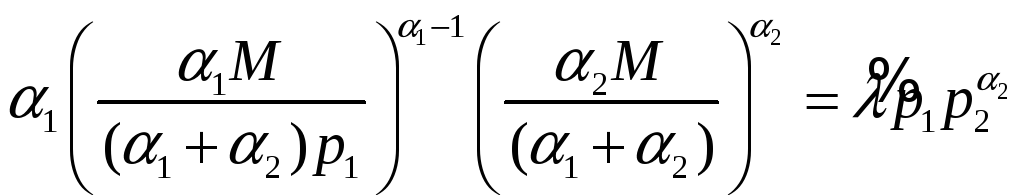откуда

.

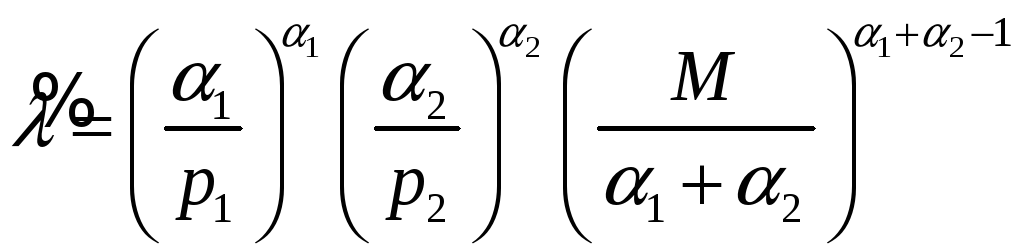Разумеется, в этой задаче ещё следует доказать, что в найденной точке есть экстремум. Для этого следует сначала вычислить второй дифференциал функции Лагранжа в точке . В рассмотренном примере, согласно (23):

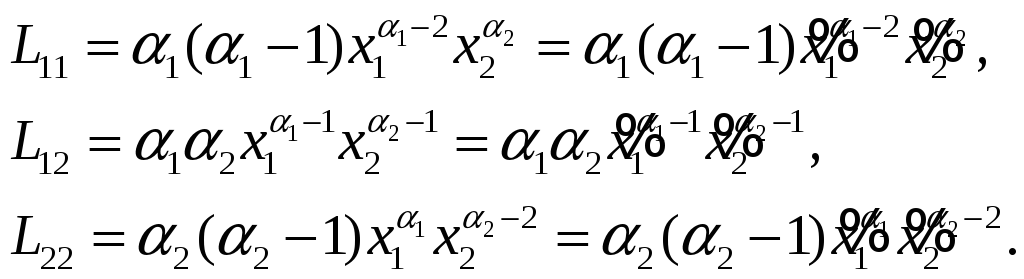
Поэтому второй дифференциал функции равен

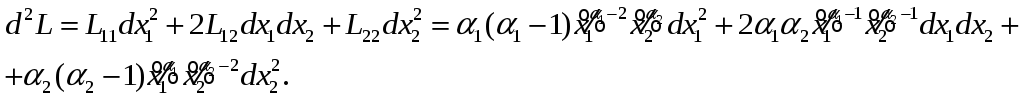
Важно учесть, что из уравнения связи следует, чтооткуда

,

поэтому

Все три слагаемых в скобках – отрицательные числа, так как .Поэтому при найденных значениях функция Лагранжа достигает наибольшего значения..

В качестве примера дадим ещё одно доказательство наличия условного экстремума, используя окаймлённый гессиан

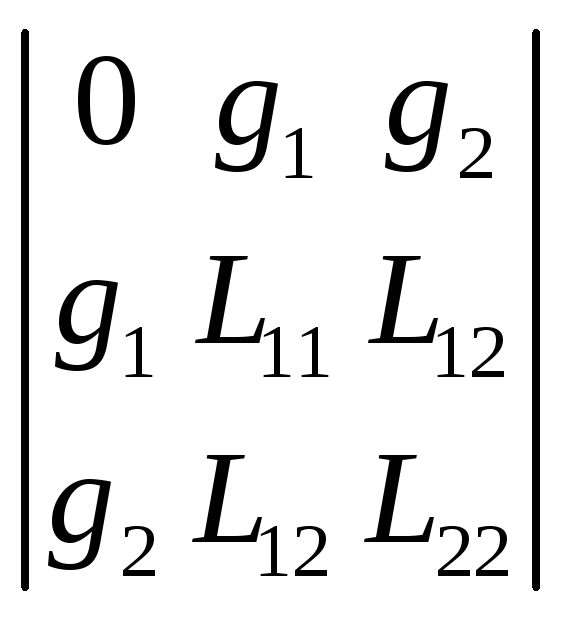
в рассматриваемом случае имеющий вид

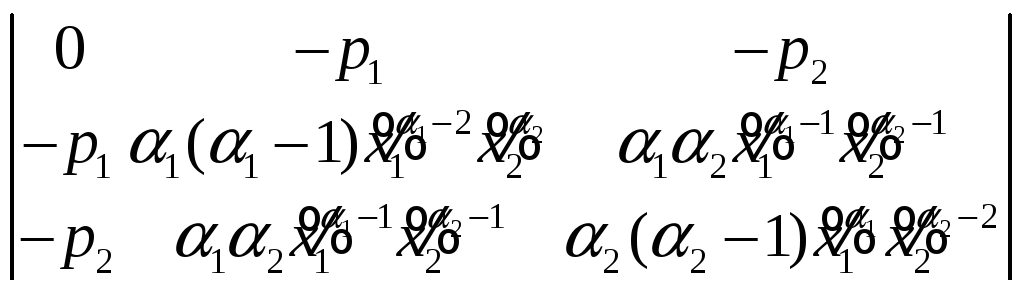
и равный

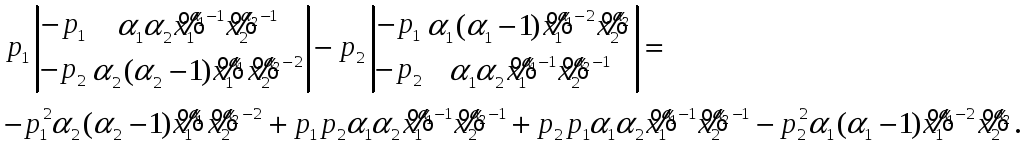
Эта величина положительная, так как , и все числа .Поэтому в рассматриваемой точке имеется максимум.

Замечание. В этой задаче уравнение связи легко решается: и задача отыскания условного экстремума сводится к задаче поиска наибольшего значения функции на отрезке .

Рекомендуем читателю применить это соображение к рассмотренному

примеру с функцией самостоятельно.