
- •Глава 3. Теория пределов
- •§ 3.1. Предел последовательности. Предел функции
- •§ 3.2. Бесконечно малые величины
- •§ 3.3. Арифметические свойства предела
- •§ 3.4. Предельный переход в неравенствах
- •§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
- •§ 3.6.Первый замечательный предел
- •§ 3.7. Предел монотонной ограниченной функции
- •§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
- •§ 3.9. Критерий Коши существования предела последовательности, предела функции
§ 3.4. Предельный переход в неравенствах
Теорема
3.4.1.
Если
функция имеет предел при
 ,
равныйА
и в некоторой проколотой окрестности
,
равныйА
и в некоторой проколотой окрестности
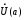 точки
a
принимает неотрицательные значения,
то
точки
a
принимает неотрицательные значения,
то
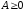 .
.
Доказательство. Будем доказывать методом от противного.
Допустим,
что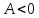 .
Возьмем
.
Возьмем .
Тогда
.
Тогда
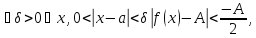
откуда
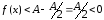
Получаем,
что для любого
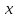 из
пересечения проколотых окрестностей
из
пересечения проколотых окрестностей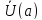 и
и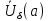 одновременно выполняются неравенства
одновременно выполняются неравенства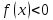 и
и .
Тем самым мы пришли к противоречию.
Теорема доказана.
.
Тем самым мы пришли к противоречию.
Теорема доказана.
Теорема
3.4.2.Если
для двух функций
 и
и
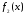 ,
имеющих пределы, соответственно,
,
имеющих пределы, соответственно,
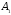 и
и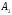 ,
в некоторой проколотой окрестности
,
в некоторой проколотой окрестности
 выполняется
неравенство
выполняется
неравенство ,
то
,
то .
.
Доказательство.
Обозначим
 .
При этом для любого
.
При этом для любого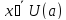 выполнено
неравенство
выполнено
неравенство
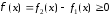 .
По теореме 3.4.1 имеем
.
По теореме 3.4.1 имеем
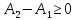 ,
т.е.
,
т.е.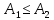 .
Теорема доказана.
.
Теорема доказана.
Замечание: Эти две теоремы означают, что при переходе к пределу сохраняется нестрогое неравенство.
Замечание:
строгое
неравенство между функциями может не
сохраниться для пределов этих функций.
Например, для функций
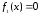 ,
,
 в
любой
в
любой
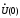 выполняется неравенство
выполняется неравенство
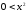 ,
т.е.
,
т.е. .
Однако,
.
Однако,
Теорема
3.4.3 (Теорема о “зажатой” переменной).
Если
 выполняется
неравенство
выполняется
неравенство ,
и если
,
и если ,
то
,
то
Доказательство. Для доказательства данной теоремы докажем лемму:
Лемма
3.4.1. Если
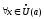 выполняется неравенство
выполняется неравенство ,
и если
,
и если ,
то и
,
то и
 .
.
Доказательство.
Требуется доказать, что:
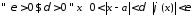 .
Дано:
.
Дано: .Выберем
число
.Выберем
число
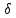 таким,
что
таким,
что ,
а также удовлетворяющим неравенству
,
а также удовлетворяющим неравенству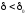 ,
из которого следует, что
,
из которого следует, что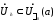 .Тогда
для всех
.Тогда
для всех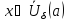 выполнены
неравенства
выполнены
неравенства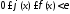 ,
что означает, что
,
что означает, что .
Лемма
доказана.
.
Лемма
доказана.
Перейдем
к доказательству теоремы и обозначим
 .
При этом
.
При этом удовлетворяют
условиям леммы.
удовлетворяют
условиям леммы.
Далее,
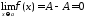 и,
по лемме,
и,
по лемме,
 .
Наконец,
.
Наконец,
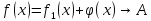 при
при (так как
(так как
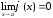 и
и
Таким образом, теорема доказана.
§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
Определение
3.5.1. Если
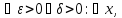

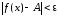 ,
то говорят, что существует предел
функции
,
то говорят, что существует предел
функции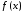 при
стремлении х к а справа
и обозначают это так:
при
стремлении х к а справа
и обозначают это так:
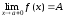 .
Аналогично, если
.
Аналогично, если

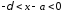 выполнено неравенство
выполнено неравенство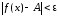 ,
, то говорят, что существует предел
функции
,
, то говорят, что существует предел
функции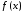 при
стремлении х к а слева
и обозначают это так:
при
стремлении х к а слева
и обозначают это так:
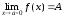 .
.
Теорема
3.5.1. Функция
 имеет при
имеет при
 предел, равный
предел, равный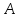 ,
тогда и только тогда, когда он имеет
пределы при стремлениих
к а справа и слева, причем оба эти пределы
равна А.
,
тогда и только тогда, когда он имеет
пределы при стремлениих
к а справа и слева, причем оба эти пределы
равна А.
Доказательство
Если
 ,
то
,
то
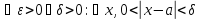
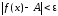 .
Поскольку из неравенств
.
Поскольку из неравенств
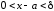 и
и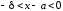 следует
неравенство
следует
неравенство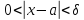 ,справедливы равенства
,справедливы равенства
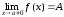 и
и
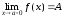 .
.
Обратно,
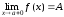 тогда и только тогда, когда
тогда и только тогда, когда
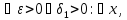
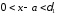
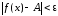 ,
а
,
а
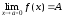 тогда и только тогда, когда
тогда и только тогда, когда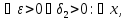
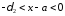
 .
.
Положим
 .
Тогда если
.
Тогда если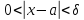 , то
, то
либо
 ,
либо
,
либо
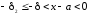
И
в том, и в другом случае
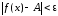 ,
т.е.
,
т.е.
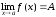 .
.
Замечание. Разумеется, для пределов справа и слева верны все теоремы об арифметических свойствах предела и о предельном переходе в неравенствах.
Определение
3.5.2. Если
 ,то
говорят, что существует предел функции
,то
говорят, что существует предел функции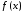 при
стремлении х к плюс-бесконечности и
обозначают это так
при
стремлении х к плюс-бесконечности и
обозначают это так

Если
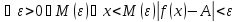 ,то
говорят, что существует предел функции
,то
говорят, что существует предел функции при
стремлении х к минус-бесконечности и
обозначают это так
при
стремлении х к минус-бесконечности и
обозначают это так

Если
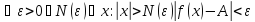 ,то
говорят, что существует предел функции
,то
говорят, что существует предел функции при
стремлении х к бесконечности и
обозначают это так
при
стремлении х к бесконечности и
обозначают это так
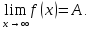
Замечание. Разумеется, для пределов при стремлении к бесконечности, перечисленных в определении 3.5.2, верны все теоремы об арифметических свойствах предела и о предельном переходе в неравенствах.
Замечание. Обратите внимание на сходство определений предела функкции при стремлении к плюс-бесконечности и предела числовой последовательности.
