4.2. Табличный симплекс-метод решения задачи линейного

программирования

4.2.1. Метод единичных векторов

Выше было показано, что основная ЗЛП, ограничения которой имеют степень неопределенности р=2, может быть решена графически. Если же ЗЛП имеет степень неопределенности p>2 , то применение для ее решения графического метода становится невозможным, так как в этом случае теряется геометрическая наглядность. Для решения таких ЗЛП применяются аналитические методы, из которых наиболее распространенным является симплекс-метод. Название метода определяется тем, что симплексом называется геометрический многогранник (многоугольник), который определяет область допустимых решений задачи.

Чтобы лучше понять идею симплекс-метода, обратим внимание на схему решения ЗЛП, которую подсказывают выводы, представленные в конце предыдущего раздела. Учитывая, что оптимальное решение ЗЛП всегда совпадает по крайней мере с одним из ее опорных решений и что опорных решений конечное число, можно наметить следующую схему нахождения оптимального решения:

а) найти все опорные решения;

б) вычислить значения функции цели, соответствующие этим опорным

решениям;

в) среди полученных значений функции цели выбрать наилучшее.

Эта схема принципиальных возражений не вызывает, однако практически ее реализовать невозможно, так как ЗЛП, встречающиеся на практике, могут иметь огромное количество опорных решений и их нахождение представляет практически непреодолимые трудности.

Симплекс-метод отличается от приведенной схемы тем, что перебор опорных решений осуществляется упорядоченно, а именно от некоторой исходной вершины многогранника переходят к такой соседней с ней вершине, которой соответствует большее (если ищется максимум) или меньшее (если ищется минимум) значение функции цели по сравнению с исходным, и т.д. Если среди соседних вершин нет таких, переход к которым сопровождается увеличением (или уменьшением) функции цели, то исходное опорное решение является оптимальным.

Итак, для начала реализации симплекс-метода надо иметь хотя бы какой-либо опорный план. В математическом программировании это достаточно сложная и самостоятельная проблема. Ниже представлены два вида табличного симплекс-метода в зависимости от способа нахождения первого опорного плана. Рассмотрим один из возможных подходов нахождения опорного плана. Однако заметим, что в любом случае симплекс-метод требует соблюдения одного условия – задача должна быть записана в основной форме.

З а д а ч а. Найти решение задачи, состоящей в определении максимального значения функции

при условиях

,

,

,

.

Видим, что задача имеет пять неизвестных и три ограничения, т.е. степень неопределенности р=2. Это означает, что два неизвестных можно принять за свободные, а три – за базисные. В данной задаче на первом шаге итерации удобно, если свободными будут переменные х₄=0, х₅=0. Тогда базисными будут остальные переменные х₁; х₂; х_3. Из ограничений следует, что в таком случае они будут иметь следующие значения:

x₁ = b₁; x₂ = b₂ ; x₃ = b₃ .

Имеем первый опорный план:

,

с которого уже можно начинать итерационный процесс симплекс-метода. В частности, при этом плане первое значение функции цели примет вид:

.

Если внимательно посмотреть на ограничения, то можно отметить специфику их записи, которая и позволяет достаточно просто определить первый опорный план. Запишем ограничения в векторной форме:

,

где вектор-столбцы Р_j имеют вид

, , , , , .

Векторы Р₁, Р₂, Р₃ – единичные векторы при переменных х₁, х₂, х₃ соответственно. Именно их в данной задаче мы приняли за базисные и не равные нулю. Векторы Р₄, Р₅ – неединичные и содержат множители при переменных х₄, х₅ , которые приняты за свободные и они приравнены нулю (вспомним, что в любой вершине симплекса ряд переменных обязательно равны нулю, их количество равно степени неопределенности задачи). В результате мы приходим к формированию первого опорного плана в представленном выше виде.

Сформулируем следующие правила реализации метода:

1. Задачу линейного программирования записывают в виде основной ЗЛП (F→max, все ограничения – равенства).

2. Оценивают степень неопределенности задачи р (число неизвестных минус число ограничений).

3. Записывают вектор-столбцы Р_j множителей при переменных.

4. Определяют единичные вектор-столбцы. Их количество должно быть не менее количества ограничений.

5. Те переменные, для которых P_j – единичные вектор-столбцы, переводятся в базисные, остальные – в свободные.

6. Базисные переменные приравниваются свободным членам ограничений х_i=b_i , свободные переменные приравниваются нулю. В сумме они образуют первый опорный план.

После такой подготовки приступают к заполнению симплекс-таблицы и решению задачи.

З а д а ч а. Найти максимальное значение функции

при ограничениях

,

,

,

.

Запишем вектор-столбцы в ограничениях

, , , , , .

Предположим, что из приведенных единичными будут векторы Р₃, Р₄, Р₅. Это означает, что коэффициенты а₁₃=а₂₄=а₃₅=1, а коэффициенты а₁₄=а₁₅=а₂₃=а₂₅=а₃₃=а₃₄=0 . Тогда переменные х₃, х₄, х₅ становятся базисными, а переменные х₁, х₂ – свободными. Последние приравниваются нулю, тогда базисные переменные принимают значения х₃=b₁, x₄=b₂, x₅=b₃, т.е. мы имеем первый опорный план Х⁽¹⁾=(0, 0, b₁, b₂, b₃). Теперь необходимо заполнить симплекс-таблицу (табл.2).

Таблица 2

Симплекс-таблица задачи линейного программирования

i	Базис	Cб	Р0	C1	C2	C3	C4	C5
				P1	P2	P3	P4	P5
1	2	3	4	5	6	7	8	9	10
1	Р3	с3	b1	а11	а12	а13=1	а14=0	а15=0	b1/a12
2	Р4	с4	b2	а21	а22	а23=0	а24=1	а25=0	b2/a22
3	Р5	с5	b3	а31	а32	а33=0	а34=0	а35=1	b3/a32
4	zj
5	∆j			z1-c1	z2-c2	z3-c3=0	z4-c4=0	z5-c5=0

Для данной задачи табл. 2 имеет 10 столбцов и пять строк. В столбец «базис» вписываются индексы векторов-столбцов тех переменных, которые в данный момент являются базисными. В нашем случае это Р₃, Р₄, Р₅. В столбец «С_б» вносятся значения ценовых множителей (со своим знаком), которые содержатся в функции цели при соответствующей базисной переменной. В столбец Р₀ записываются значения базисных переменных для рассматриваемого опорного плана (в первой симплекс-таблице это свободные члены в уравнениях ограничений). В последующие столбцы записываются значения соответствующих вектор-столбцов. Видим, что только по свободным переменным в столбцах Р_j (j=1…5) есть конкретные числа, а по столбцам при базисных переменных – только по одной единице, в остальных клетках – нули.

После заполнения таблицы необходимо выполнить расчеты. Они включают следующее.

1. По столбцам Р₀ – Р₅ рассчитывается сумма произведений стоящей в соответствующей клетке цифры на ценовой коэффициент с , стоящий при i-ой переменной из базиса (в данном случае i=1…3). Эта сумма обозначена через индекс z_j.

2. По столбцам Р₁ – Р₅ определяют разность между суммами z_j и ценовым коэффициентом c_j по каждой переменной и эта сумма записывается в строке 5 под индексом ∆_j.

3. После выполнения предыдущих операций проводят анализ данного опорного плана. Если в результате расчетов все ∆_j ≥ 0, то данный опорный план является оптимальным. В противном случае следует искать другой опорный план.

4. Если какой-либо ∆_j меньше нуля, то данный столбец называется разрешающим столбцом. Это означает, что переменная при данном вектор-столбце должна из свободной перейти в базисную. Если столбцов с отрицательными ∆_j больше одного, то выбирают тот, в котором абсолютное значение ∆_j максимально ( по базисным переменным ∆_j обязательно будут равны нулю).

5. Если все элементы вектора Р в разрешающем столбце отрицательные, то данная задача решения не имеет, так как целевая функция не ограничена, т.е. область допустимых решений не замкнута.

Если в результате первой итерации установлено, что задача может иметь другой опорный план, происходит переход к следующему опорному плану. Он заключается в том, что определяется переменная, которая должна быть переведена из свободной в базисную. Такая переменная определяется по минимальному (с учетом знака) значению ∆_j (см. пункт 4). Если, например, таковой окажется ∆₂ ≤ 0 → min , то это означает, что вторая переменная должна быть переведена из свободных в базисную. Остается установить, взамен какой переменная х₂ должна быть введена в базис.

Для этого надо выполнить дополнительные расчеты фактора t по каждой базисной переменной. Он определяется путем деления значения данной переменной (находится в столбце Р₀ ) на соответствующий для данной переменной коэффициент а_ij из разрешающего столбца (принимаются во внимание только положительные коэффициенты). Результаты расчетов записываются в столбец 10. Из полученного набора t_i выбирается минимальное значение. Предположим, что t₂=min. Это означает, что переменная х₄ должна быть выведена из базисных и переведена в свободные (т.е. х₄=0), а на ее место необходимо поместить переменную х₂ ≠ 0. Тогда очередной опорный план будем искать в виде Х⁽²⁾=(0, х₂, х₃, 0, х₅).

Для такого плана составляется новая таблица, где каждая клетка рассчитывается по особому алгоритму. С этой целью введем еще два понятия: строка выводимой базисной переменной называется разрешающей строкой, а коэффициент а_ij, стоящий на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом. В нашем случае разрешающей будет вторая строка, а разрешающим элементом – коэффициент а₂₂.

Очередная симплекс-таблица имеет прежнюю форму, но другое содержание. Прежде всего в новой таблице заполняется разрешающая строка, т.е. в данном случае вторая, где будет стоять новый базис. Для этого все элементы старой строки (Р₀ – Р₅) делят на величину разрешающего элемента (в данном случае на а₂₂), при этом в столбец «базис» вписывается обозначение базиса новой переменной (Р₄ заменяется на Р₂), в третий столбец «С_б» вписывается из функции цели величина коэффициента с₂. Элементы остальных строк (по векторам Р₀ – Р₅) в новой таблице вычисляют по правилу треугольника. Оно заключается в следующем (рис.4).

Имеются :

1. две строки - преобразованная с новой базисной переменной (строка нового базиса в новой симплекс-таблице, рис.4), и преобразуемая строка одной из старых базисных переменных (в старой симплекс-таблице);

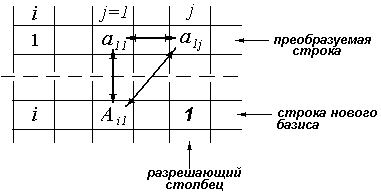
Рис.4. К обоснованию “правила треугольника”

2. два столбца – столбец (например, j=1), по которому происходит замена элементов, и разрешающий столбец j.

Заменяют элемент а₁₁ в первой строке на новое его содержание А₁₁ :

,

или значение нового элемента в преобразуемой строке равно его старому значению минус произведение элемента того же столбца в строке нового базиса на элемент, стоящий в разрешающем столбце преобразуемой строки.

В новой симплекс-таблице проводят расчеты z_j , ∆_j и делают заключение о новом опорном плане. Если подтверждается его оптимальность, то значения базовых переменных в оптимальном плане будут находиться в столбце “ Р₀ “, а свободные переменные будут иметь нулевое значение. По этим данным рассчитывают значение функции цели, хотя эта цифра будет уже находиться в таблице в ячейке на пересечении столбца “ Р₀ “ и строки z_j. Рассмотрим на примере практическую реализацию описанных выше процедур, а также проясним физический смысл некоторых параметров и процедур.

З а д а ч а 5. Для изготовления различных изделий А, В, С предприятие использует три различных вида сырьевых материалов. Нормы расхода сырья каждого вида на производство одного изделия каждого вида, цена одного изделия, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведено в таблице 3. Изделия А,В,С, могут производиться в любых соотношениях, но производство ограничено имеющимися ресурсами. Необходимо составить план выпуска изделий, при котором, максимально используя имеющийся запас сырьевых материалов, общая стоимость всей произведенной продукции будет максимальной.

Таблица 3

Технологическая программа производства

Вид сырья	Нормы затрат сырья на одно изделие			Запас сырья
	А	В	С
I	18	15	12	360
II	6	4	8	192
III	5	3	3	180
Цена изделия	9	10	16
План выпуска	х1	х2	х3

На основании вышерассмотренных задач (в частности, задачи 1) составим математическую модель ЗЛП в стандартной форме: найти максимальное значение функции при ограничениях

,

,

.

По своему экономическому содержанию переменные могут принимать только неотрицательные значения:

.

Запишем эту задачу в форме основной ЗЛП. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений:

,

,

.

Эти дополнительные переменные по экономическому смыслу означают неиспользуемое в данном плане производства количество сырья соответствующего типа. Преобразованную систему уравнений запишем в векторной форме:

,

где , , , , , , .

Поскольку среди векторов Р_j (j=1…6) при трех ограничениях имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план . Иначе говоря, х₁=х₂=х₃=0 – свободные переменные, х₄=360, х₅=192, х₆=180 - базисные переменные. Последние образуют базис трехмерного векторного пространства, что делает решение задачи графическим методом невозможным.

Составляем симплекс-таблицу для первой итерации, подсчитываем z_j; ∆_j; t_i и проверяем исходный план на оптимальность.

Таблица 4

Первая симплекс-таблица к задаче 5

i	Базис	Сб	Р0	С1=9	С2=10	С3=16	С4=0	С5=0	С6=0	ti
				Р1	Р2	Р3	Р4	Р5	Р6
1	2	3	4	5	6	7	8	9	10	11
1	Р4	0	360	18	15	12	1	0	0	30
2	Р5	0	192	6	4	8	0	1	0	24
3	Р6	0	180	5	3	3	0	0	1	60
4	zj		0	0	0	0	0	0	0
5	∆j			-9	-10	-16	0	0	0

Прежде всего определяем разрешающий столбец. Так как в строке ∆_j есть три отрицательных числа, то проверяемый план не будет оптимальным. Минимальным из них является ∆_j= -16,следовательно, разрешающим будет столбец 7. Это означает, что переменную х₃ следует перевести из свободных в базисные. Все элементы вектор-столбца Р₃ положительные, поэтому рассчитываем t_i :

, , .

Минимальное значение фактора t приходится на базис Р₅. Это означает, что переменную х₅ следует перевести из базисных в свободные, а на ее место поместить переменную х₃. Рассмотрим некоторые аспекты содержания таблицы, которые позволяют конкретизировать физический смысл представленных в ней величин.

Как видно из табл.4, значения всех основных переменных х₁, х₂, х₃ равны нулю (в первом опорном плане это свободные переменные), а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Такие значения переменных отвечают “плану”, при котором ничего не производится, сырьевые материалы не используются и значение целевой функции будет нулевым (в таблице z=0 по четвертому столбцу), т.е. выручка от производственной деятельности отсутствует. Этот план, конечно, не является оптимальным. Это видно и из строки 5, так как в ней имеется три отрицательных числа: ∆₁ = - 9, ∆₂ = - 10, ∆₃ = - 16. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, насколько увеличится эта сумма при введении в план единицы того или иного вида продукции. Так, число -9 означает, что при включении в план производства одного изделия А произойдет увеличение доходной части на 9 руб. Очевидно, что наиболее целесообразно ввести в план изделие С, так как при этом доходная часть будет увеличиваться наиболее динамично (на 16 руб на каждое изделие). Именно этим объясняется решение ввести в базис ту переменную, для которой │∆j│=max .

Находя значения фактора t, получают частное от деления “ресурс/ед.затраты”, т.е. это количество j-го изделия, которое можно было бы изготовить, если весь объем данного ресурса потратить только на это изделие. Например,

означает, что, если мы введем в план производства изделие С (т.е. в базис вводится переменная х₃), то всего запаса сырьевых материалов первого типа у нас хватит на 30 изделий. Расчет

означает, что по второму ресурсу мы могли бы изготовить изделий типа С уже не 30, а всего 24. Соответственно, используя только третий тип ресурса, можно изготовить уже 60 изделий типа С. Становится ясно, сколько максимум изделий типа С можно позволить выпустить – это 24 изделия. В противном случае у нас не хватит второго ресурса. Следовательно, надо в план включать изделие С и в количестве не более 24, т.е. выводить из плана базисный вектор Р₅ и принадлежащие ему ресурсы передавать изделию С, а это означает: переменная х₃ вводится в базис взамен переменной х₅, выводимой в свободные. В результате имеем следующий опорный план

.

Составим новую симплекс-таблицу, учитывая, что разрешающий столбец – столбец под номером 7, разрешающая строка – строка под номером 2, разрешающий элемент – число 8, лежащее в клетке на пересечении этих строки и столбца.

Таблица 5

Вторая симплекс-таблица к задаче 5

i	Базис	Сб	Р0	С1=9	С2=10	С3=16	С4=0	С5=0	С6=0	ti
				Р1	Р2	Р3	Р4	Р5	Р6
1	2	3	4	5	6	7	8	9	10	11
1	Р4	0	360-24∙12=72	18-12∙6/8=9	15-12∙4/8=9	12-1∙12=0	1-0∙12=1	0-12∙1/8= -3/2	0-12∙0=0	8
2	Р3	16	192/8=24	6/8	4/8	1	0	1/8	0	48
3	Р6	0	180-24∙3=108	5-3∙6/8=11/4	3-3∙4/8=3/2	3-3∙1=0	0-3∙0=0	0-3∙1/8= -3/8	1-3∙0=1	72
4	zj		16∙24=384	16∙6/8=12	16∙4/8=8	16∙1=16	0	16∙1/8=2	0
5	∆j			12-9=3	8-10=-2	0	0	2	0

В результате конкретизировали второй опорный план:

,

т.е. из реальных изделий предполагается выпуск только изделия типа С в объеме 24 шт. Очевидно, что и этот план также неоптимален: в строке значений ∆_j есть одно отрицательное значение, а именно ∆₂=-2 (т.е. столбец 6 - разрешающий). Значит, в новом плане надо переменную х₂ перевести в базис. Все элементы старого базиса Р₂ - неотрицательные числа, поэтому по всем строкам (1,2,3) рассчитаны значения фактора t. Минимальное значение t₁=8 означает, что из базиса должна быть удалена переменная х₄ (т.е. строка 1 - разрешающая строка, тогда разрешающий элемент равен 9) и весь освобождающийся объем сырьевого материала первого вида передается на изготовление второго изделия в объеме 8 шт. Тогда на третьем шаге итерации будем искать план в виде:

.

В табл. 6 представлены результаты пересчета симплекс-таблицы на третьем шаге итерации. Так как все ∆_j≥ 0, то мы имеем оптимальный план:

.

Функция цели приняла значение F_max=400 (расположено в ячейке на пересечении четвертой строки и четвертого столбца).

Таблица 6

Третья симплекс-таблица к задаче 5

i	Базис	Сб	Р0	С1=9	С2=10	С3=16	С4=0	С5=0	С6=0	ti
				Р1	Р2	Р3	Р4	Р5	Р6
1	2	3	4	5	6	7	8	9	10	11
1	Р2	10	8	1	1	0	1/9	-1/6	0
2	Р3	16	20	1/4	0	1	-1/18	5/24	0
3	Р6	0	96	5/4	0	0	-1/6	-1/8	1
4	zj		400	14	10	16	2/9	5/3	0
5	∆j			5	0	0	2/9	5/3	0

Результаты показывают, что оптимальный план производства не должен предусматривать изготовление изделия вида А (причина этого рассматривается ниже), изделий вида В надо выпустить в объеме 8 шт, а изделий вида С – в количестве 20 шт. Полученное значение х₆=96 указывает на то, что при анализируемом плане производства будет недоиспользован третий вид сырьевых материалов в объеме 96 ед. Действительно, если подставить значения переменных в первичные ограничения по ресурсам, то получим:

,

,

.

Видим, что ресурсы первого и второго вида использованы в полном объеме, а третий вид ресурса недоиспользован именно в объеме 96 ед., т.е. на предприятии этот вид ресурсных материалов находится в избытке.

Для экономии времени и повышения наглядности решение ЗЛП табличным способом можно проводить, представляя все расчеты в одной таблице. Ниже приведена обобщенная симплекс-таблица для выше рассмотренной задачи, в которой представлены результаты расчетов сразу по всем трем итерационным этапам.

Таблица 7

Обобщенная симплекс-таблица к задаче 5

i	Базис	Сб	Р0	С1=9	С2=10	С3=16	С4=0	С5=0	С6=0	ti
				Р1	Р2	Р3	Р4	Р5	Р6
1	2	3	4	5	6	7	8	9	10	11
1 2 3 4 5	Р4 Р5 Р6 zj ∆j	0 0 0	360 192 180 0	18 6 5 0 -9	15 4 3 0 -10	12 8 3 0 -16	1 0 0 0 0	0 1 0 0 0	0 0 1 0 0	30 24 60
1 2 3 4 5	Р4 Р3 Р6 zj ∆j	0 16 0	72 24 108 384	9 6/8 11/4 12 3	9 4/8 3/2 8 -2	0 1 0 16 0	1 0 0 0 0	-3/2 1/8 -3/8 2 2	0 0 1 0 0	8 48 72
1 2 3 4 5	Р2 Р3 Р6 zj ∆j	10 16 0	8 20 96 400	1 1/4 5/4 14 5	1 0 0 10 0	0 1 0 16 0	1/9 -1/18 -1/6 2/9 2/9	-1/6 5/24 -1/8 5/3 5/3	0 0 1 0 0

З а д а ч а 6. Найти максимум функции при условиях

,

,

,

.

Р е ш е н и е. Систему уравнений задачи запишем в векторной форме:

,

где , , , , , , .

Так как при трех ограничениях имеем три единичных вектора (Р₃, Р₄, Р₆), можем сформировать первый опорный план

,

в котором базисные переменные примут значения: х₃=20, х₄=24, х₆=18. Составим симплекс-таблицу 8 и все дальнейшие расчеты запишем в нее.

На первом шаге итерации видим, что исследуемый опорный план не является оптимальным и он может быть улучшен. Разрешающий столбец (9) и разрешающая строка (2) определяют, что в базис надо ввести х₅ взамен выводимого в свободные х₄ и следующий опорный план будем искать в виде:

Таблица 8

Симплекс-таблица к задаче 6

i	Базис	Сб	Р0	С1=2	С2= -6	С3=0	С4=0	С5=5	С6=0	ti
				Р1	Р2	Р3	Р4	Р5	Р6
1	2	3	4	5	6	7	8	9	10	11
1 2 3 4 5	Р3 Р4 Р6 zj ∆j	0 0 0	20 24 18 0	-2 -1 3 0 -2	1 -2 -1 0 6	1 0 0 0 0	0 1 0 0 0	1 3 -12 0 -5	0 0 1 0 0	20 8 -
1 2 3 4 5	Р3 Р5 Р6 zj ∆j	0 5 0	12 8 114 40	-5/3 -1/3 -1 -5/3 -11/3	5/3 -2/3 -9 -10/3 8/3	1 0 0 0 0	-1/3 1/3 4 5/3 5/3	0 0 1 0 0	0 0 1 0 0

.

На втором шаге итерации при разрешающем элементе 3 пересчитана таблица и опять видим, что данный опорный план также не является оптимальным. Имеем разрешающий столбец 5. Но так как он содержит только отрицательные числа, делаем вывод, что эта задача решения не имеет.