lekcii_dm

	Пусть М –	множество	всех	непрерывных	функций	на отрезке
,	èëè Ñ , .	Положим f	g f t g t äëÿ		t , .	Это будет
частичная упорядоченность функций из Ñ , .
	Множество всех подмножеств			некоторого множества М частично

упорядочено по включению, то есть M1 M2 означает M1 M2 . Множество всех натуральных чисел частично упорядочено, если a b

означает “b делится без остатка на а”.

Определение.

Элемент а называется максимальным, если из a b следует, что b a .

Определение.

Элемент а называется минимальным, если из c a следует, что c a .

Определение.

Частично упорядоченное множество, для любых двух точек а, b которого найдется следующая за ними точка с (a c,b c), называется

направленным.

Определение.

Пусть:

1.М и M ' – частично упорядоченные множества;

2.f :M â M '.

3.Отображение f :M â M ' сохраняет порядок, то есть если из a b ,

где a M ,b M ' f a f b .

Тогда.

21

Отображение f :M â M ' называется изоморфизмом частично упорядоченных множеств М и M ', если оно

1.биективно (существует взаимооднозначное соответствие между элементами множеств М и M ');

2.соотношение f (a) f (b) a b .

Пример.

Пусть М – множество натуральных чисел, частично упорядоченное по

“делимости”;

M ' — множество натуральных чисел, упорядоченное естественным

образом, то есть b a ,	если b a – неотрицательное число,	то есть
b a 0.
Тогда отображение	íà	числу n
	f :M M ' n n , то есть ставящее
его само:

1.сохраняет порядок;

2.не является изоморфизмом.

Замечание.

Отношение изоморфизма между частично упорядоченными множествами представляет собой отношение эквивалентности (рефлексивность, транзитивность, симметричность). Следовательно, какоелибо множество частично упорядоченных множеств можно разбить на классы изоморфных между собой подмножеств.

Определение.

22

То общее, что присуще любым двум изоморфным между собой частично упорядоченным множествам, называется порядковым типом.

Определение.

Пусть М – частично упорядоченное множество;

a M ,b M ;

не выполняется ни одно из соотношений a b и b a . Тогда а и b называются несравнимыми элементами.

Определение.

Если в частично упорядоченном множестве М несравнимых элементов нет, то множество М называется упорядоченным (линейно упорядоченным, совершенно упорядоченным), то есть если оно:

частично упорядочено;

для a M ,b M имеет место a b либо b a .

Замечания.

Всякое подмножество упорядоченного множества само упорядочено. Так как упорядоченность есть частный случай частичной

упорядоченности, то можно говорить о порядковом типе упорядоченного множества.

Примеры.

Пусть = 1,2,3,... – множество натуральных чисел с естественным отношением порядка. Его порядковый тип обозначают .

23

Если два частично упорядоченных множества изоморфны между собой, то они, конечно, имеют одинаковую мощность, так как изоморфизм – это биекция. Следовательно, можно говорить о мощности, отвечающей данному порядковому типу, например, типу отвечает мощность 0. Однако обратное неверно, так как множество данной мощности может быть упорядочено, вообще говоря, многими разными способами.

Порядковый тип линейно упорядоченного конечного множества однозначно определяется числом n его элементов и обозначается n.

Для счётного множества натуральных чисел возможен такой тип: 1,3,5, ,2,4,6, , то есть любое чётное число следует за любым нечётным, при этом чётные и нечётные числа упорядочены по возрастанию.

1.07. Счётные множества. Теорема Кантора.

Все множества можно разделить на конечные и бесконечные.

Вкачестве первых можно привести, например, 1) множество всех вершин некоторого многогранника; 2) множество всех простых чисел, не превосходящих данного числа; 3) множество молекул воды в данный момент на Земле и т.д.

Вкачестве бесконечных множеств можно указать, например, множество всех натуральных чисел; множество всех многочленов с рациональными коэффициентами и т.д.

Определение.

Множество называется бесконечным, если из него можно извлечь один

элемент, два элемента и т.д., причём после каждого такого шага в этом множестве ещё останутся элементы.

Определение.

24

Счётное множество – это такое множество, элементы которого биективно сопоставимы со всеми натуральными числами, то есть это – множество, элементы которого можно занумеровать в бесконечную последовательность: а1, а2, а3,…, аn,….

Примеры счётных множеств.

Множество всех целых чисел.

Установим биекцию между множествами натуральных и целых чисел следующим образом:

0 –1 1 –2 2 …,

1 2 3 4 5 …, то есть n 2n + 1, при n 0;

n 2|n|, при n 0.

Множество всех чётных положительных чисел, так как n 2n – биекция.

Множество степеней числа 2: 2, 4, 8,…,2n,… при показателе степени n 1. Здесь биекция – это: 2n n, то есть

а1 = 2, а2 = 4, а3 = 8,… .

4. Множество всех рациональных чисел. Каждое рациональное число записывается в виде = qp , q > 0, p и q – взаимно простые целые числа.

Назовем сумму |p| + q высотой рационального числа . Ясно, что число дробей с данной высотой n конечно. Например, высоту 1 имеет только число

10, высоту 2 – два числа 11и 11, высоту 3 – четыре числа: 12 , 12 , 12 , 12 и т.д. Таким образом, каждому рациональному числу можно сопоставить некоторый порядковый номер. Следовательно, множество рациональных чисел счётно.

25

Определение.

Бесконечное множество, не являющееся счётным, называется несчётным множеством.

Теорема.

Всякое подмножество счётного множества конечно, или счётно.

Доказательство:

Пусть А – счётное множество, В – его подмножество. Занумеруем элементы множества А: а1, а2, а3,…, аn,…. Пусть an1,an2,...– те из них, которые входят в В. Если среди чисел n1,n2, есть наибольшее, то В – конечно, в противном случае В – счётно, так как его члены an1,an2,...

занумерованы числами 1,2, .

Теорема.

Сумма любого конечного или счётного множества счётных множеств есть снова счётное множество.

Доказательство:

Пусть А1,А2, – счётные множества. Не нарушая общности, будем считать, что они попарно не пересекаются, в противном случае следует рассмотреть множества А1,А2 \ А1,А3 \(А1 А2), и т.д. Эти множества являются также не более, чем счётными, так как всякое подмножество счётного множества конечно или счётно, а сумма этих множеств равна сумме множеств А1,А2, .

Итак, рассмотрим множества А1,А2, . Элементы этих множеств можно записать в виде бесконечной таблицы

26

а11 а12 а13 а14 а21 а22 а23 а24 а31 а32 а33 а34 , а41 а42 а43 а44

где в i-той строке стоят элементы множества Аi . Занумеруем элементы множеств “по диагоналям”, то есть за первый элемент примем а11, за второй - а12 , за третий – а21 и т.д., двигаясь по стрелкам:

а11	а12	а13	а14
а21	а22	а23	а24
а	а	а	а	.
31	32	33	34
а41	а42	а43	а44

Таким образом, каждый элемент каждого из множеств получит определенный номер, то есть будет установлено взаимно-однозначное соответствие между всеми элементами всех множеств А1,А2, и всеми натуральными числами. Теорема доказана.

Теорема.

Всякое бесконечное множество содержит счётное подмножество.

Доказательство:

Пусть М – бесконечное множество. Выберем в нём произвольный элемент а1. Так как множество М – бесконечно, в нём a2 а1, а также а3,

отличный от а1	и а2 и т.д. Продолжая этот процесс, получаем счётное
подмножество	A {а1, а2 …} множества М, что и требовалось доказать.
Определение.

27

Два множества М и N называются эквивалентными (М N), если между их элементами можно установить взаимно однозначное соответствие.

Определение.

Множество М называется счётным, если оно эквивалентно множеству натуральных чисел.

Ясно, что два множества, эквивалентные третьему, эквивалентны между собой.

Примеры.

1. Множества точек на любых двух отрезках a,b и c,d эквивалентны между собой (рис. 1.5).

Рис. 1.5. Точки p и q соответствуют друг другу, так как они являются проекциями одной и той же точки r вспомогательного отрезка ef.

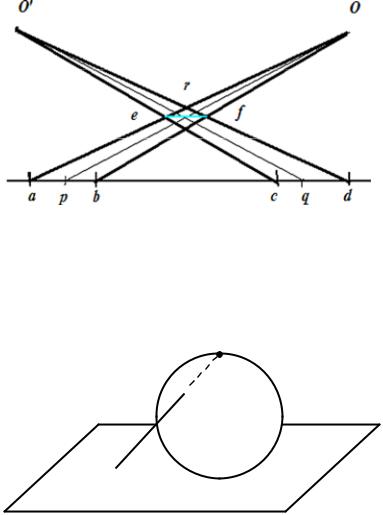
2. Множество всех точек на плоскости множеству точек на сфере

(рис. 1.6).

N

z

Рис. 1.6. Биекция z устанавливается с помощью стереографической

28

проекции.

3. Множество всех чисел в интервале (0,1) эквивалентно множеству всех точек на прямой (рис. 1.7).

π		1
				1
2		2

					0
												0
																		0
		-	π						-	1
										2
			2
															y =	1	arctgx +			1
	y = arctgx						y =	1		arctgx
																				2

Рис. 1.7. Биекция устанавливается, например, с помощью функции у 1 arctgx 12.

Замечания.

Иногда бесконечное множество оказывается эквивалентным своей истинной части, например:

1.Натуральные числа эквивалентны множеству всех целых чисел.

2.Натуральные числа эквивалентны множеству рациональных чисел.

3.На интервале (0,1) столько же точек, сколько и на всей прямой.

Теорема.

Всякое бесконечное множество эквивалентно некоторому своему собственному подмножеству.

Доказательство:

Согласно известной теореме: из всякого бесконечного множества М

можно выбрать счётное подмножество. Пусть	А а1,а2, – такое
подмножество. Разобьём множество А на два	счётных подмножества:
A1 а1,а3,а5 и A2 а2,а4,а6 .

29

Между А и А1 можно установить биекцию:

n 2n 1, где n A, 2n 1 A1 .

Рассмотрим множества:

1. A М \ А М ; 2. А1 М \ А М \ А2 .

Установив взаимно однозначное соответствие между А и А1, легко продолжить это соответствие на рассматриваемые множества, отнеся каждому элементу множества М \ А сам этот элемент. Таким образом, установлено взаимнооднозначное соответствие между множествами М и М \ А2. Теорема доказана.

Теорема Кантора.

Для любой последовательности {аn } действительных чисел из любого интервала I существует точка p из I такая, что p an при всех n.

Доказательство:

много способов доказательства этой теоремы. Рассмотрим один из

них.

	Возьмем отрезок I1 I такой,	что a1 I1. Затем берём отрезок I2 I1
такой, что a2 I2 . Продолжая процесс по индукции, выберем в			In 1 отрезок
In	такой, что an In . Полученная последовательность вложенных отрезков
In	имеет непустое пересечение. Если	p In , то p I и p an	при всех n,
		n

что и требовалось доказать.

Следствие из теоремы Кантора.

Ни один интервал не является счётным множеством.

Впервые доказательство нёсчетности этого множества Кантор привёл в 1873 г.

Примеры несчётных множеств.

1. Множество всех точек любого отрезка a,b или интервала (а,b).

30