lekcii_dm

Определение

Аналогично определяется минимальный маршрут в нагруженном графе.

Замечание

Задачи поиска минимального пути имеет смысл ставить тогда, когда нет отрицательных замкнутых путей (иначе можно повторять цикл многократно, уменьшая «длину»).

Свойства минимальных путей в нагруженном орграфе

1.	Если для дуги	x X l(x) 0, то min путь (маршрут) является
простой цепью;
2.	если 1, 2 ,..., k	min путь (маршрут) то для i,j : 1 i j k путь

(маршрут) i i 1... j 1 j тоже является min

Доказывается аналогично св-вам ненагруженного графа.

3. если v...uw min путь (маршрут) среди путей (марш.) из v в w, содержащих не более k+1 дуг (ребер), то v...u min путь (маршрут) из v в u среди путей (марш.), содержащих не более k дуг (ребер).

Поиск min пути.

			k	,
Пусть D=(V,X) – нагр. орграф, V={v1,… vn}, n>1. Введем величины i
где i=1,…,n, k=1,2,…,n-1.
	k	равна длине min пути
Для каждого фиксированного i и k величина i
		k	.
среди путей из v1 в vi содержащих не более k дуг. Если путей нет, то i
Положим также 0 0,	0 ,i 2,...n .
1	i

81

Введем матрицу длин дуг C(D)=[cij] порядка n, причем

l vi ,v j ,		vi ,v j X ,
cij		vi ,v j X .

Утверждение.

При i=2,…,n, k 0 выполняется равенство

k 1	k	c ji (Принцип динамического программирования.
i	min j
	1 j n

Использовать его позволяют свойства 2,3 min путей).

Алгоритм Форда-Беллмана

Для нахождения min пути в нагруженном орграфе D из v1 в vi.(i 1). ( ik записываем в виде матрицы, i- строка, k-столбец).

1)Составляем табл. ik , i=1,…,n, k=0,…,n-1. Если in 1 , то пути из v1 в vi нет. Конец алгоритма.

2)Если in 1 то это число выражает длину любого min пути из v1 в

vi. Найдем min k1 1, при котором ik1 in 1 . По определению ik получим, что k1- min число дуг в пути среди всех min путей из v1 в vi.

3) Затем определяем номера i2,…, ik1 1 такие, что

i2k1 1 ci2,i ik1 ,i3k1 2 ci3,i2 i2k1 1 ,

. . . . . . . . . . . . .

ik01 1 cik1 1,ik1 i1k1 ,

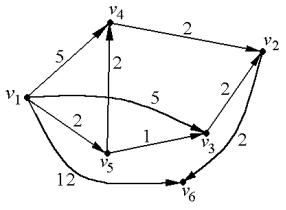
Пример. v1 v6

82

	v1	v2	v3	v4	v5	v6
v1			5	5	2	12
v2						2
v3		2
v4		2
v5			1	2
v6

Путь v1 v6

7=5+2 (2-ая стр.) 5=3+2 (3-я стр.) 3=1+2 (5-я стр.) 2=0+2 (1-я стр.)

Путь v1 v5 v3 v2 v6

0	1	2	3	4	5
i	i	i	i	i	i
0	0	0	0	0	0
		7	5	5	5
	5	3	3	3	3
	5	4	4	4	4
	2	2	2	2	2
	12	12	9	7	7

83

2.16. Специальные пути в орграфах (маршруты в графах).

Существует редко применяемый сейчас метод задания графа в виде латинской матрицы. В этом способе направление дуг задается порядком букв в их названии.

Определение.

Свойство называется латинским, если из того, что путь = 1 2, где1, 2 (множество всех путей в орграфе) обладает свойством , следует, что пути 1, 2 также обладают свойством .

Примеры латинских свойств.

1)Не проходить через данную вершину (или через множество вершин).

2)Не проходить через данную дугу (или через множество дуг).

3)Быть простой цепью (или простым контуром).

4)Быть цепью (или контуром).

5)Не проходить через каждую вершину более k раз.

Определение.

Матричный способ перечисления путей в орграфе, обладающих заданным латинским свойством , называют методом латинской комбинации.

Введем бинарную операцию . Пусть 1=v1v2…vk (мн-во путей, обладающих свойством ), 2=w1w2…wL . Положим

					,	если v		w	и путь				обладаетсвойством б
1 2		1	,	2			k	1		1		2
									в противном случае.

84

lijk

(lijk

Положим = = .

Введем латинскую матрицу L k lijk размерности n n такую, что

—множество путей длины k из vi в vj, обладающих свойством ,

, если таких путей нет).

Определение.

Под	k	m		будем	понимать
	результатом комбинации C L L
квадратную матрицу C=[cij] порядка n с элементами
n
cij lirk lrjm (аналогично произведению			матриц:		строка на

r 1

столбец).

Утверждение.

При любом k 1 выполняется L k L k 1 L1 L1 L1 L1

Пример.

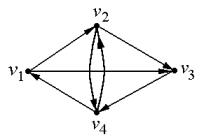
Найти все простые цепи длины 3 в орграфе D:

85

1	2	1		1
L	L	L	L

		v1v2					v1v3
							v2v3	v2v4
								v3v4
v4v1		v4v2
	3			2			1
	L			L		L

		v1v2v3	v1v2v4
			v1v3v4
v2v4v1			v2v3v4
v3v4v1	v3v4v2
	v4v1v2	v4v1v3
		v4v2v3

	v1v3v4v2		v1v2v3v4
v2v3v4v1		v2v4v1v3
	v3v4v1v2
		v4v1v2v3

Найти простые контура длины 4 в том же орграфе (свойство ).

Для этого

используем

матрицу L 3 ,

полученную при решении

предыдущей задачи

4

3

1

L

L

L

v1v2

v1v3

v2v3

v2v4

v3v4

v4v1

v4v2

v1v3v4v2

v1v2v3v4

=

v2v3v4v1

v2v4v1v3

v3v4v1v2

v4v1v2v3

86

v1v2v3v4v1
	v2v3v4v1v2
		v3v4v1v2v3
			v4v1v2v3v4

2.17. Эйлеровы цепи и цепи.

река остров остров

Нужно пройти по всем мостам по одному разу и вернуться обратно..

Утверждение.

Если в псевдографе G имеется хотя бы одно ребро и отсутствуют висячие вершины, то G содержит хотя бы один простой цикл.

Доказательство

Если в G имеется петля, то это уже цикл, если в G есть кратные ребра, то это тоже цикл. Допустим, что петель и кратных ребер нет.

Пусть v1 и v2 – произвольные смежные вершины. Будем строить последовательность v1, v2, v3… такую, что для любого i>2 вершины vi, vi-1 смежны и vi vi-1 (т.к. в G нет висячих вершин, то эту последовательность можно продолжать неограниченно). Но рано или поздно какая-то из вершин повторится. Это и будет искомый цикл.

87

Утверждение.

Для того чтобы связный псевдограф G обладал эйлеровым циклом необходимо и достаточно чтобы степени всех его вершин были четными.

См. алгоритм.

Утверждение.

Для того чтобы связный псевдограф G обладал эйлеровой цепью необходимо и достаточно, чтобы он имел ровно 2 вершины нечетной степени.

(Нужно соединить начало и конец. Тогда задача сводится к предыдущей).

Алгоритм выделения эйлерова цикла в связном мультиграфе с четными степенями вершин

1)Выделим из G цикл 1. (т.к. степени верш. четны, то висячие верш. отсутствуют). Положим l=1, G’=G.

2)Удаляем из G’ ребра, принадлежащие выделенному циклу. Полученный псевдограф снова обозначаем G’. Если в G’ отсутствуют ребра, то переходим к шагу 4.

3)Выделяем из G’ цикл. Присваиваем l:=l+1 и переходим к шагу 2.

4)По построению выделенные циклы содержат все ребра по одному разу. Если l:=1, то искомый эйлеров цикл найден (конец работы алгоритма).

Впротивном случае находим циклы, содержащие хотя бы по одной общей вершине (в силу связности графа это всегда можно сделать). Склеиваем эти циклы. Повторяем эти операции, пока не останется один цикл. Он и является искомым.

88

Пример.

Задача о Кенигсбергских мостах не имеет решения, т.к. есть вершины с нечетными степенями.

2.18. Гамильтовы циклы.

Эйлеровы циклы характеризуются тем, что существуют циклы, содержащие каждое ребро один раз. Гамильтовы циклы определяются для конечно связных графов аналогичным образом, но только по отношению к вершинам.

Определение.

Простой цикл называется гамильтовым, если он проходит через каждую вершину графа.

Определение.

Гамильтовой цепью в графе называется простая цепь, проходящая через все вершины по одному разу.

89

Пример:

Так называемая задача о бродячем торговце (коммивояжёре) также является задачей относящихся к гамильтовым цепям. Будем говорить, что простая цепь полная, если её нельзя продолжить при помощи добавления рёбер к какому-нибудь из концов.

Теорема.
Полная простая	цепь длины	l имеет тип цикла, если
a0 a1 l 1, где	a – локальная	степень вершины a .

Теорема.

Максимальная (длиннейшая) простая цепь в связном графе может иметь тип цикла только тогда, когда граф имеет гамильтов цикл.

Теорема.

90