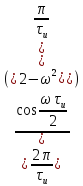6. Примеры определения спектральной плотности сигналов

Ниже приводится краткое описание некоторых сигналов и опре­деляются их спектральные плотности. При определении спектраль­ных плотностей сигналов, удовлетворяющих условию абсолютной интегрируемости, пользуемся непосредственно формулой (4.41).

Спектральные плотности ряда сигналов приведены в табл. 4.2.

1) Импульс прямоугольной формы (табл. 4.2, поз. 4). Колебание, изобра­женное на рис. (4.28, а), можно записать в виде

.

Его спектральная плотность

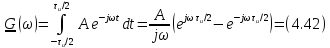
График спектральной плотности (рис. 4.28, а) построен на основе прове­данного ранее анализа спектра периодической последовательности однополярных, прямоугольных импульсов (4.14). Как видно из (рис. 4.28, б), функция обра­щается в нуль при значениях аргумента = n, где п - 1, 2, 3, ... — лю­бое целое число. При этом угловые частоты равны  = .

Рис. 4.28. Импульс прямоугольной формы (а) и его спектральная плотность (б)

Спектральная плотность импульса при численно равна его площади, т.еG(0)=A. Это положение справедливо для импульса s(t) произвольной формы. Действительно, полагая в общем выражении (4.41) = 0, получим

т. е. площадь импульса s(t).

Таблица 4.3.

№ п/п	Сигнал s(t)			Спектральная плотность
1	2	3	4		5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16		-
17

При растягивании импульса расстояние между нулями функциисокращается, т. е. происходитсжатие спектра. Значение при этом возра­стает. Наоборот, при сжатии импульса происходит расширение его спектра а значение уменьшается. На (рис. 4.29, а, б) приведены графики амплитудного и фазового и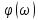 спектров прямоугольного импульса.

Рис. 4.29. Графики амплитудного (а) Рис. 4.30. Импульс прямоугольной формы, и фазового (б) спектров сдвинутый на время

При сдвиге импульса вправо (за­паздывание) на время (рис. 4.30) фазовый спектр изменяется на величи­ну, определяемую аргументом множителяexp() (табл. 4.2, поз. 9). Результирующий фазовый спектр запаздывающего импульса изо­бражен на рис. 4.29, б пунктирной ли­нией.

2) Дельта-функция (табл. 4.3, поз. 9). Спектральную плотность – функции находим по формуле (4.41), используя фильтрующее свойствоδ-функции:

Таким образом, амплитудный спектр равномерный и определяется пло­щадьюδ-функции [= 1], а фазовый спектр равен нулю [= 0].

Обратным преобразованием Фурье от функции = 1 пользуются как одним из определенийδ-функции:

или

Пользуясь свойством временного сдвига (табл. 4.2, поз. 9), определяем спект­ральную плотность функции , запаздывающей на время относительно:

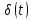Амплитудный и фазовый спектры функции показаны в табл. 4.3, поз. 10. Обратное преобразование Фурье от функции имеет вид

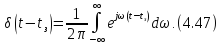
3) Гармоническое колебание (табл. 4.3, поз. 12). Гармони­ческое колебание не является абсолютно интегрируемым сигналом. Тем не ме­нее для определения его спектральной плотностиприменяют прямое пре­образование Фурье, записывая формулу (4.41) в виде:

Тогда с учетом (4.47) получаем

где

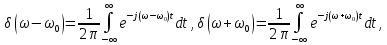
δ(ω) – дельта-функции, смещенные по оси частот на частоту , соответственно вправо и влево относительно. Как видно из (4.48), спектральная плотность гармонического колебания с конечной амплитудой принимает бесконечно боль­шое значение на дискретных частотахи.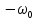

Выполняя аналогичные преобразования, можно получить спектральную плотность колебания (табл. 4.3, поз. 13)

(4.49)

4) Функция вида (табл. 4.3, поз. 11)

Спектральная плотность сигнала в виде постоянного уровня А определяется по формуле (4.48), положив = 0:

5) Единичная функция (или единичный скачок) (табл. 4.3, поз. 8). Функция не является абсолютно интегрируемой. Если представить как предел экспоненциального импульса ,т. е.

то спектральную плотность функцииможно определить как предел спектральной плотности экспоненциального импульса (табл. 4.3, поз. 1) при :

Припервое слагаемое в правой части этого выражения равно нулю на всех частотах, кроме= 0, где оно обращается в бесконечность, а площадь под функцией равна постоянной величине

Поэтому пределом первого слагаемого можно считать функцию . Преде­лом второго слагаемого является функция. Окончательно получим

Наличие двух слагаемых в выражении (4.51) согласуется с представлением функции в виде 1/2+1/2sign(t).Постоянной составляющей 1/2 со­гласно (4.50) соответствует спектральная плотность , а нечетной функции — мнимое значение спектральной плотности .

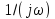При анализе воздействия единичного скачка на цепи, передаточная функция которых при = 0 равна нулю (т. е. на цепи, не пропускающие по­стоянный ток), в формуле (4.51) можно учитывать только второе слагаемое, представляя спектральную плотность единичного скачка в виде

6) Комплексный экспоненциальный сигнал (табл. 4.3, поз. 16). Если представить функциюв виде

то на основании линейности преобразования Фурье и с учетом выражений (4.48) и (4.49) спектральная плотность комплексного экспоненциального сигнала

Следовательно, комплексный сигнал 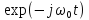обладает несимметричным спект­ром, представленным одной дельта-функцией, смещенной на частотувправо относительно.

7) Произвольная периодическая функция. Представим произвольную перио­дическую функцию (рис. 4.31, а) комплексным рядом Фурье

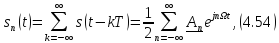
где — частота следования импульсов.

Коэффициенты ряда Фурье

выражаются через значения спектральной плотности одиночного импуль­са s(t) на частотах (n=0,±1, ±2, ...). Подставляя (4.55) в (4.54) и поль­зуясь соотношением (4.53), определяем спектральную плотность перио­дической функции:

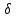Согласно (4.56) спектральная плотность произвольной периодической функции имеет вид последовательности-функций, смещенных друг от­носительно друга, на частоту (рис. 4.31, б). Коэффициенты при δ-функциях изменяются в соответствии со спектральной плотностьюодиночного им­пульсаs(t) (пунктирная кривая на рис. 4.31,б).

8) Периодическая последовательность δ-функций (табл. 4.3, поз. 17). Спект­ральная плотность периодической последовательности –функций

определяется по формуле (4.56) как частный случай спектральной плотности периодической функции при = 1:

Рис.4.31. Произвольная последовательность импульсов (а) и её спектральная плотность (б)

Рис. 4.32. Радиосигнал (а), спектральные плотности радиосигнала (в) и его огибающей (б)

и имеет вид периодической последовательности δ-функций, умноженных на ко­эффициент .

9) Радиосигнал с прямоугольной огибающей. Радиосигнал, представленный на (рис. 4.32,а), можно записать как

Согласно поз. 11 табл.4.2 спектральная плотность радиосигнала полу­чается путем сдвига спектральной плотности прямоугольной огибающей по оси частот на вправо и влево с уменьшением ординат в два раза, т. е.

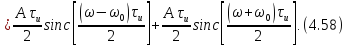
Это выражение получается из (4.42) путем замены частоты на частоты– сдвиг вправо и— сдвиг влево. Преобразование спектра огибающейпоказано на (рис. 4.32, б, в).

Примеры расчета спектров непериодических сигналов приведены так же в [7].