Задача о загрузке емкости. Теоретические положения

Задача о загрузке емкости предметами различной конфигурации является одной из задач раздела «Динамическое программирование».

Пусть емкость грузоподъемностью загружается предметами различных типов. — вес предмета -го типа, — его ценность, , причем под ценностью не обязательно понимается стоимость предметов.

Необходимо определить оптимальный вариант загрузки емкости, максимизирующий общую ценность груза при ограничениях по объему.

Составим математическую модель задачи:

Найти максимум функции при ограничении ,

где — число предметов -го типа загружаемых в емкость, .

При загрузке предметов 1-го типа имеем:

при

(квадратные скобки в формуле означают, что берется целая часть от деления.) и тогда

—максимальная стоимость груза.

При загрузке предметов 1-го и 2-го типов имеем:

если было загружено предметов второго типа, то вес предметов первого типа не должен превышать . Их ценности соответственно равны и , тогда:

—общая максимальная ценность груза.

Данное выражение аналогично функциональному уравнению Беллмана, т.е. задача ЦП (целочисленного программирования) сведена к задаче ДП (динамического программирования).

Пример

Пусть ; ; ;

Этап №1:

Загружаем предметы первого типа:

т.к. , то

0	0	0
1	4	1
2	8	2
3	12	3
4	16	4
5	20	5

Этап №2:

Загружаем предметы первого и второго типа:

т.к. , то;

0	0	0	0
1	4	0	1
2	9	1	0
3	13	1	1
4	18	2	0
5	22	2	1

Этап №3:

Загружаем предметы всех трех типов:

т.к. , то

0	0	0	0	0
1	4	0	0	1
2	9	0	1	0
3	13	1 или 0	0 или 1	0 или 1
4	18	0	2	0
5	22	1 или 0	1 или 2	0 или 1

Максимальная стоимость груза – 22 единицы – достигается при двух вариантах загрузки: , , или , , . Кроме того, получены оптимальные решения для любых значений в интервале от 0 до 5 (характерная черта метода ДП).

Порядок работы

1. Составить алгоритм расчёта загрузки ёмкости и реализовать его на языке Pascal (выбор другого языка программирования с разрешения преподавателя).

2. Предъявить результаты выполнения п.1 на контроль преподавателю.

Содержание отчёта

1. Отчётом по данной лабораторной работе является файл с исходным текстом программы с проставленными копирайтами.

Задача о наборе высоты и скорости летательным аппаратом. Теоретические положения

Одной из задач динамического программирование является задача об оптимальном режиме набора высоты и скорости летательным аппаратом.

Пусть некий летательный аппарат, находящийся на высоте и имеющий скорость , должен быть поднят на заданную высоту , а его скорость должна быть доведена до заданного значения . Известен расход горючего для подъема с любой высоты на любую высоту при неизменной скорости , и расход топлива для увеличения скорости с до при неизменной высоте .

Требуется найти оптимальный режим набора высоты и скорости, при котором общий расход горючего будет минимален.

Для простоты допустим, что весь процесс набора высоты и скорости разделён на ряд последовательных шагов (этапов) и за каждый шаг самолёт увеличивает только высоту или только скорость.

Будем изображать состояние объекта точкой на плоскости (рис. 3.1), где абсцисса – скорость объекта, а ордината – его высота.

Рис.3.1

Для решения задачи методом ДП разобьём отрезок на, а отрезок на частей (этапов). Число частей n и m принципиального значения не имеет и может быть выбрано исходя из требований к точности задачи.

Так как за каждый шаг мы можем менять либо высоту либо скорость, то общее число шагов будет: .

Чтобы оптимизировать управление процессом набора высоты и скорости, надо знать расход горючего на каждом шаге. Прежположим, что эти расходы заданы (см. рис. 3.2). На каждом отрезке записан расход горючего в условных единицах.

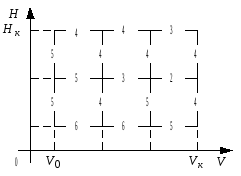
Рис. 3.2

Количество шагов в данном случае: .

Будем оптимизировать расход топлива начиная с последнего, 5-го шага.

Рассмотрим отдельно правый верхний угол нашей прямоугольной сетки, с конечной точкой. В эту точку за один шаг можно переместиться из двух соседних точек и , причем из каждой – только одним способом. Если предпоследний шаг привел нас в точку , то мы должны двигаться по горизонтали и тратить 3 единицы топлива; если в – идти по вертикали и тратить 4 единицы топлива. Запишем эти минимальные (в данном случае неизбежные) расходы в кружках, которые поставим в точках и . Запись «3» в кружке у означает: «если мы пришли в , то минимальный расход топлива, переводящий нас в точку , равен 3 единицам». Аналогичный смысл имеет запись «4» в кружке у точки. Оптимальное направление, приводящее к этому помечено в каждом случае стрелкой выходящей из кружка.

Таким образом, условное направление на последнем шаге найдено для любого исхода предпоследнего шага. Для каждого из этих исходов найден, кроме того, условный минимальный расход топлива. За счет которого можно переместиться в точку Sк.

Перейдем к планированию предпоследнего, 4-го шага. Для этого рассмотрим все возможные результаты пред-предпоследнего 3-го шага. После этого шага мы можем оказаться только в одной из 3-х точек C₁, C₂, C₃. Из каждой такой точки мы должны найти оптимальный путь в точку Sк и соответствующий этому пути минимальный расход топлива.

Если мы оказались в точку C₁, то выбора нет, и мы должны двигаться в по горизонтали и тратить 4+3=7 единиц топлива. Для точки C₃ аналогично, мы можем двигаться по вертикали и тратить 4+4=8 единиц горючего. Для C₂ есть выбор: из нее мы можем перейти к Sк либо через точку B₁, либо через точку B₂. В первом случае мы израсходуем 4+3=7 единиц топлива, а во втором 2+4=6 единиц топлива. Значит, оптимальный путь из С₂ в Sк начинается горизонтальным участком, а минимальный расход топлива составит 6 единиц.

Таким образом, переходя от точке к точке справа налево и сверху вниз (от конца к его началу), можно для каждой узловой точки выбрать оптимальное направление на следующем шаге, то есть направление, ведущее из данной точки в точку Sк с минимальным расходом топлива.

Чтобы найти в узловой точке оптимальное направление, нужно рассмотреть два возможных пути из этой точки и для каждого из них найти сумму расхода топлива на этом шаге и минимального расхода топлива на оптимальном продолжении пути, уже построенном для следующей точки, куда ведет данный путь. Из двух путей выбирается тот, для которого сумма меньше (если суммы равны, то выбирается любой путь).

Значение в точку So будет равно значению минимального расхода топлива, необходимого для выполнения условий изменения высоты и скорости.