3. Модель Эйнштейна

Эта модель была разработана Эйнштейном до модели Дебая. Для простоты Эйнштейн предположил, что кристалл с N атомами обладает 3N модами колебаний с одинаковой угловой частотой 𝜔_E.

Он использовал эту частоту в качестве подгоночного параметра для согласования своей модели теплоемкости с экспериментальными данными для твердых тел. Каждой колебательной моде соответствует одна и та же энергия <E>, определяемая как средняя энергия квантового осциллятора

(22)

Общая колебательная энергия решетки равна по модели Эйнштейна

(23)

(В (23) отсутствует энергии нулевых колебаний, которая в модели Эйнштейна не учитывалась).

Соответствующая теплоемкость при постоянном объеме равна

(24)

где F_E — функция Эйнштейна, равная

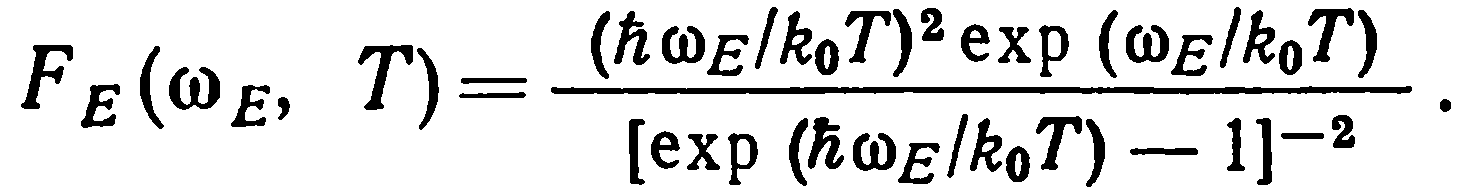(25)

Функция Эйнштейна стремится к единице при высоких температурах, что приводит к классическому результату, т. е. при высоких температурах по модели Эйнштейна

(26)

Это хорошо известный закон Дюлонга и Пти

Однако при температурах значительно ниже характеристической температуры Эйнштейна, T<<Т_E=ħ𝜔/k, теплоемкость убывает экспоненциально:

(27)

Модель Эйнштейна слишком упрощена. Частоты атомов осцилляторов выбраны одинаковыми. При низких температурах расходится с экспериментом. Эксперименту более соответствует модель Дебая.

2. Теплопроводность

Корпускулярный или фононный подход к рассмотрению колебаний решетки особенно удобен при изучении процессов с преобразованием энергии. Эти процессы включают процессы рождения и уничтожения фононов. Теплопроводность удобнее всего описывать на языке рассеяния фононов на других фононах, статических несовершенствах решетки или на электронах.

1. Решеточная теплопроводность и длина свободного пробега фононов

Тепловая энергия может передаваться в кристалле фононами, фотонами, свободными электронами (или свободными дырками), электронно-дырочными парами, экситонами (связанными электронно-дырочными парами).

Электронная компонента теплопроводности в металлах обычно является доминирующей. Однако в неметаллических кристаллах большая часть теплового потока переносится колебаниями решетки (фононами); лишь при самых высоких температурах преобладающим процессом может стать передача энергии фотонами. Рассмотрим поток фононов, который возникает при наличии в кристалле градиента температур.

Вспомним, что, согласно выражению (6), при температуре Т количество возбуждаемых фононов с волновым вектором к и угловой частотой 𝜔 равно

, (28)

что соответствует статистике Бозе-Эйнштейна.

В условиях теплового равновесия, если нет температурных градиентов, <n_k> = <n_-k>, т. е. существует полное равенство скоростей фононных потоков в любых двух взаимно противоположных направлениях. Таким образом, общий тепловой поток равен нулю.

Когда имеется температурный градиент теплопроводность можно выразить через 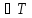и скорость потока энергии — через единичную площадку, перпендикулярную градиенту температуры:

(29)

Эту теплопроводность можно выразить через микроскопические характеристики фононов, воспользовавшись аналогией между проводимостью фононного газа и обычного молекулярного газа. Выражение для теплопроводности в рамках кинетической теории газов для простейшего случая, когда все частицы имеют одинаковые скорости (что справедливо для фононов при температурах много ниже температуры Дебая), записывается в виде

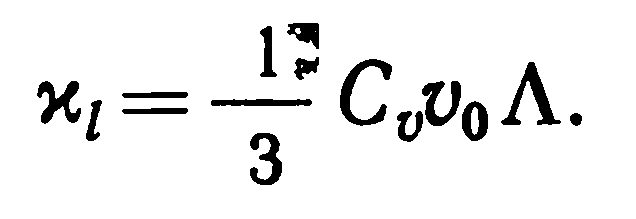(30)

Здесь Cv — теплоемкость решетки для единицы объема, которая является мерой плотности фононов, v₀ — скорость фононов (скорость звука), а Λ — средняя длина свободного пробега фононов.

Длина пути, проходимого фононом с момента его рождения до момента уничтожения или иного превращения, часто сильно зависит от его энергии. Она может быть довольно большой для фононов малых энергий, но становится весьма малой для фононов, энергия которых превышает пороговую энергию процессов переброса kθ_u (о которой мы скажем ниже). Тем не менее, для любого распределения фононов всегда можно определить среднюю длину свободного пробега Λ с помощью выражения (30).

Для температур вблизи точки плавления Λ может уменьшаться до 6—10 межатомных расстояний. При очень низких температурах Λ может достигать 1 мм. Общий вид температурной зависимости Λ и соответствующая зависимость показаны на рис. 5. Мы должны установить, как ведет себя Λ(T), чтобы понять поведение теплопроводности.

В табл. 2 приведены значения теплопроводности и длины свободного пробега для трех неметаллических твердых тел при трех различных температурах. Значения длины свободного пробега фононов вычислены по формуле (30) с использованием данных по скорости звука (см. табл. 1) и теплоемкости. Последняя определялась по температурам Дебая, приведенным в табл. 1. Из табл. 2 видно, в каком широком интервале возможно изменение длины свободного пробега фононов.

Таблица 2. Теплопроводность решетки и средняя длина свободного пробега фонона в неметаллических кристаллах

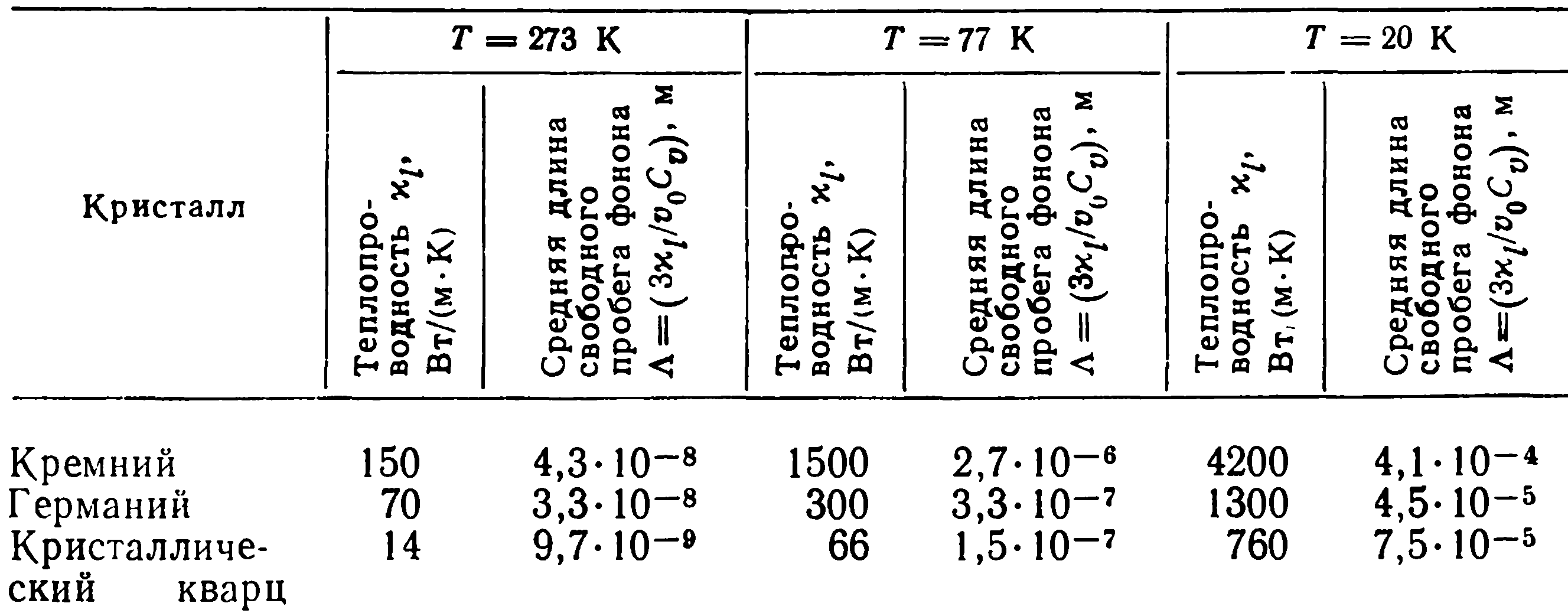
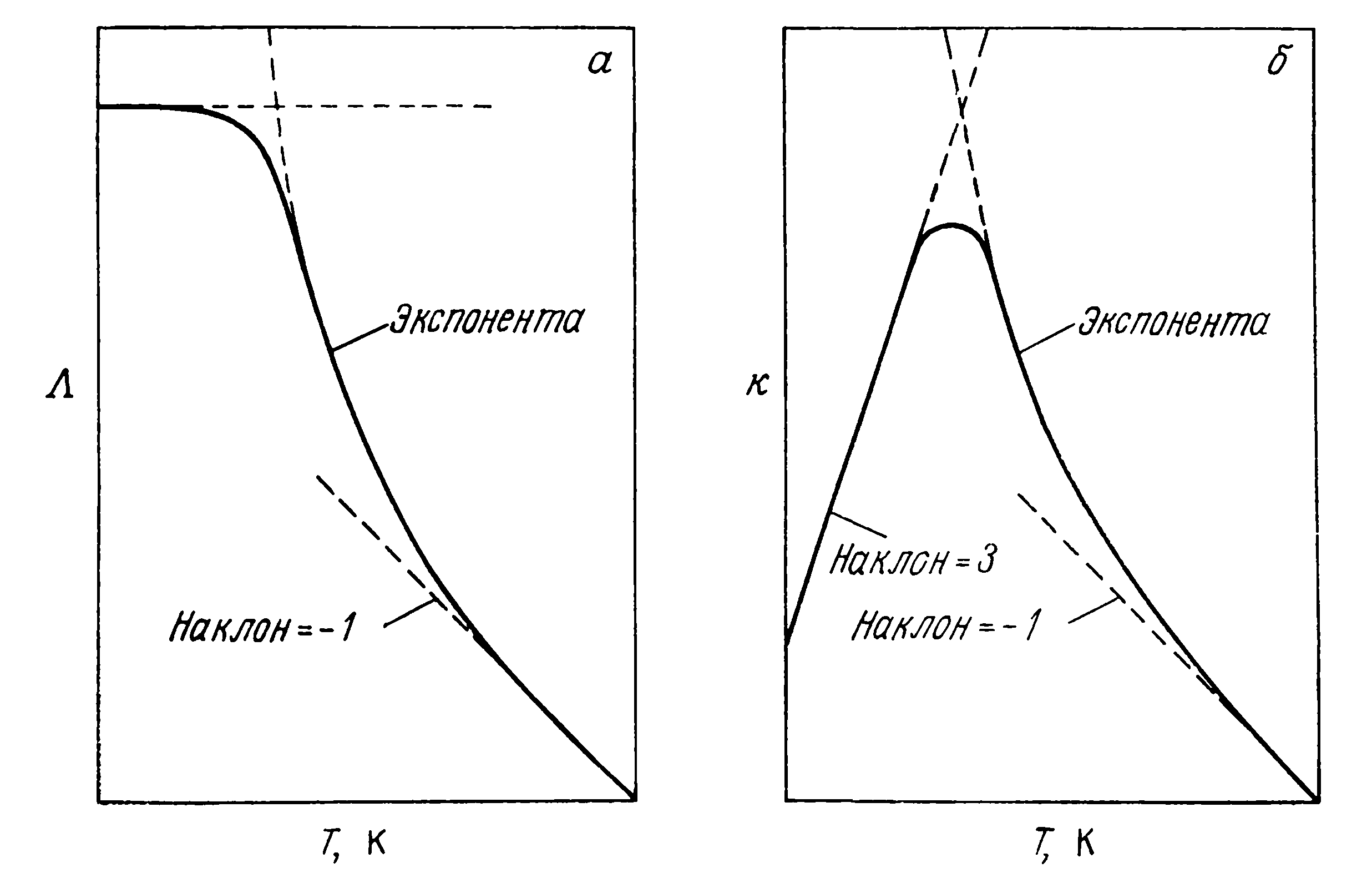
Рис. 5. Типичные кривые зависимости средней длины Λ свободного пробега фонона и фононной теплопроводности от температуры в двойном логарифмическом масштабе. Увеличение средней длины свободного пробега при понижении температуры, связанное с уменьшением вероятности процессов переброса (U-процессов), прекращается, когда существенным становится рассеяние фононов на дефектах кристаллической решетки и поверхности кристалла.