9) Свойства отношений (рефлексивность, симметричность, антисимметричность, транзитивность, эквивалентность), теорема о свойствах композиции отношений.

В силу свойства ассоциативности обычно композицию отношений обозначают (P◦Q)◦R  PQR.

Бинарное отношение R на множестве А называется рефлексивным, если для любого его элемента a выполняется aRa: a   aRa.

Бинарное отношение R на множестве А называется антирефлексивным, если для любых его элементов a,b aRb  a  b.

Бинарное отношение R на множестве А называется симметричным, если из его выполнения для a, b следует выполнение для b, a:  a, b   aRb  bRa.

Бинарное отношение R на множестве А называется антисимметричным, если из его выполнения для a, b и b, a следует, что a и b совпадают.  a, b   aRb и bRa  a = b.

Бинарное отношение R на множестве А называется транзитивным, если из его выполнения для a,b и для b,c следует его выполнение для a,c:  a, b, c   aRb и bRc  aRc.

Бинарное отношение R на множестве А называется полным, или линейным, если для любых двух различных элементов множества A оно выполняется или для a, b, или для b, a:  a, b   | ab  aRb или bRa.

Отношение R на множестве A²:

1. R рефлексивно  I  r;

2. R симметрично  R = R^–1;

3. R транзитивно  R◦R  R;

4. R антисимметрично  R  R^–1  I;

5. R полно  R  I  R^–1 = U;

Доказательство:

1.  R рефлексивно  aA выполняется aRa, т.е. (a,a)R. Но множество всех таких a составляет I  IR.  IR  aA {(a,a)}=I  (a,a)R, т.е. R рефлексивно.

2.  R симметрично  a,bA | (a,b)R  (b,a)R. Но если (a,b)R  (b,a)R^–1 по определению обратного отношения. Поскольку это справедливо для любых a,b, то R  R^–1 и R^–1  R  R^–1 = R.  R^–1 = R  RR^–1 и R^–1R  a,bA | (a,b)R  (a,b)R^–1 и (a,b)R^–1  (a,b)R. Если (a,b)R, то по определению (b,a)R^–1, значит, (b,a)R, т.е. a,bA | (a,b)R (b,a)R, что и означает симметричность.

3.  R транзитивно  a,b,cA | (a,b)R и (b,c)R  (a,c)R. Но по определению композиции R◦R {(a,b) |  cA | (a,c)R и (c,b)R}  по определению транзитивности, эта пара (a,b)R, т.е. R◦RR.  Если R◦RR, то это значит, что a,bA | (a,b)R◦R эта пара (a,b)R. По определению композиции, R◦R {(a,b) |  cA | (a,c)R и (c,b)R}, но было показано, что (a,b)R,  R транзитивно.

4.  От противного. Пусть R  R^–1  I. Значит,  ab| (a,b)R и (a,b)R^–1, т.е. в пересечении существует общий элемент (a,b). Но если (a,b)R^–1, то (b,a)R. Получили, что  ab | (a,b)R и (b,a)R. По условию, R антисимметрично  a,bA | (a,b)R и (b,a)R  a=b. Получено противоречие:  ab … a=b.  R  R^–1  I  (a,bA | (a,b)R и (a,b)R^–1  (a,b)I  a=b). Но (a,b)R^–1(b,a)R  ((a,b)R и (b,a)R  a=b)  антисимметричность.

10) Представление отношений в ЭВМ и проверка свойств отношений с помощью матриц.

Удобным способом представления отношений в ЭВМ является матричная форма. Рассмотрим два конечных множества A={a₁,a₂,…,a_m}, B={b₁,b₂,…,b_n} и бинарное отношение P  AB . Определим матрицу [P] = (p_ij) бинарного отношения P по следующему правилу: Полученная матрица содержит полную информацию о связях между элементами и позволяет представлять эту информацию на компьютере.

• Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.

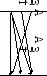
4. Рассмотрим отношение P на множестве A², где A={1,2,3} (см. иллюстрацию). Матрица этого отношения

Основные свойства матриц бинарных отношений:

1. Если бинарные отношения P,Q  AB, [P] =(p_ij), [Q] = (q_ij), то [PQ] = (p_ij+q_ij), [PQ] = (p_ij·q_ij), где умножение осуществляется обычным образом, а сложение – по логическим формулам (т.е. 0+0=0, во всех остальных случаях 1). Итак: [PQ] = [P]+[Q], [PQ] = [P]*[Q].

5. Пусть отношения P и Q заданы: . Тогда матрица их суммы [PQ] = [P]+[Q] = , матрица произведения: [PQ] = [P]*[Q] = .

2. Если бинарные отношения P  AB, Q  BC, то [P◦Q] = [P]·[Q] , где умножение матриц [P] и [Q] осуществляется по обычному правилу, а произведение и сумма элементов из [P] и [Q] – по правилам пункта 1.

3. Матрица обратного отношения P^–1 равна транспонированной матрице отношения P: [P^–1]=[P]^T.

4. Если PQ, [P]=(p_ij), [Q]=(q_ij), то p_ij  q_ij. i,j.

5. Матрица тождественного отношения единична: [I_A] = (I_ij) :  I_ij =1  i=j.

6. Пусть R – бинарное отношение на A². Отношение R называется рефлексивным, если xA (x,x)R, т.е. I_AR (на главной диагонали R стоят единицы). Отношение R называется симметричным, если x,yA (x,y)R  (y,x)R, т.е. R^–1=R, или [R]=[R]^T (матрица симметрична относительно главной диагонали). Отношение R называется антисимметричным, если R R^–1 I_A, т.е. в матрице [R R^–1]=[R]*[R]^T вне главной диагонали все элементы равны 0. Отношение R наз. транзитивным, если (x,y)R, (y,z)R (x,z)R, т.е. R◦RR.

6. Пусть отношение P на множестве A², где A={1,2,3}, задано матрицей . Поскольку на главной диагонали есть нулевые элементы, отношение не рефлексивно. Поскольку матрица не симметрична, отношение тоже не является симметричным. Проверим его антисимметричность, для чего возьмем транспонированную матрицу и вычислим [PP^–1] = [P]*[P]^T =. Все элементы вне главной диагонали равны 0, отношение антисимметрично. Проверим транзитивность по матрице: выполняется ли [P◦P]  [P]? [P◦P] =  отношение транзитивно.

11) Отношение эквивалентности и разбиения.

1. Отношение эквивалентности

Бинарное отношение R на множестве А называется отношением эквивалентности, если оно является рефлексивным, симметричным и транзитивным. Обычно отношение эквивалентности обозначают через  или ~.

7. 1. Отношения равенства чисел и множеств, равномощности множеств являются отношениями эквивалентности. 2. Отношение подобия на множестве треугольников является тривиальным отношением эквивалентности. 3. Отношение эквивалентности – на множестве программ: {(a,b) | программы a, b вычисляют одну и ту же функцию на определенной машине}.

Пусть R – отношение эквивалентности на множестве А. Определим класс эквивалентности [x] для xA: [x] = {y | xRy}, т.е. это множество всех элементов A, которые R-эквивалентны x.

Пусть E – эквивалентность на множестве M. Тогда семейство классов эквивалентности множества M называется фактормножеством множества M по отношению E и обозначается M /E ={E(x)| xM}.

8. Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы. Тогда фактормножество множества всех студентов СибГУТИ по этому отношению эквивалентности представляет собой множество всех студ. групп СибГУТИ.

Утверждение 1.1. Всякое отношение эквивалентности на множестве M определяет разбиение множества M, причем среди элементов разбиения нет пустых; и обратно, всякое разбиение множества M, не содержащее пустых элементов, определяет отношение эквивалентности на множестве M:

  M²   ß= {B_i | B_i  M, B_i  , M = B_i и  i,j ij  B_iB_j=}.