ДМ Практикум

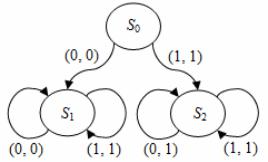
а) 11111;

б) 01111;

в) 11100;

г) 10011.

Рисунок 9.8

9.20 К.д.а. задан таблицей переходов-выходов:

S\X	0	1	2
1	2/1	5/0	5/1
2	1/1	2/0	5/1
3	3/0	7/1	3/0
4	4/0	2/1	5/0
5	2/1	1/0	2/1
6	2/1	4/1	6/0
7	7/0	3/1	7/0

Состоянию 4 эквивалентны состояния…

а) 3 и 7;

б) только 3;

в) только 7;

г) в к.д.а. нет состояний, эквивалентных состоянию 4.

91

Глава X. Элементы комбинаторики

Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определен- ным условиям. Такие задачи называют комбинаторными.

Многие из комбинаторных задач могут быть решены с помощью правил умножения и сложения.

Правило умножения: если из некоторого конечного множества первый объект (элемент A ) можно выбрать n1 способами и после каждого такого выбо- ра второй объект (элемент B ) можно выбрать n2 способами, то оба объекта ( A и B ) в указанном порядке можно выбрать n1 × n2 способами.

Правило сложения: если некоторый объект A можно выбрать n1 спосо- бами, а объект B можно выбрать n2 способами, причем первые и вторые спо- собы не пересекаются, то любой из указанных объектов ( A или B ) можно вы- брать n1 + n2 способами.

Пример 10.0. Сколькими способами можно выбрать: а) одну гласную и одну согласную букву из слова «интеграл»; б) две гласных или две согласных буквы из слова «интеграл»?

а) В слове «интеграл» 3 гласных и 5 согласных, следовательно, одну гласную и одну согласную буквы можно выбрать 3 ×5 =15 способами.

б) По правилу умножения две гласные буквы можно выбрать 3 × 2 = 6 , а две согласные - 5 × 4 = 20 способами. По правилу сложения две гласные или две

согласные можно выбрать 6 + 20 = 26 способами.
Существуют две схемы выбора k элементов из исходного множества n
элементов ( 0 < k £ n ): без возвращения (без повторений)	и с возвращением (с

повторением). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все k элементов или последовательно отбирать их по одному. Во втором случае выбранный элемент обязательно возвращается в ис- ходное множество на каждом шаге.

Схема выбора без возвращений

Пусть дано множество, состоящее из n различных элементов. Размещением из n элементов по k элементов ( 0 < k £ n ) называется лю-

бое упорядоченное подмножество данного множества, состоящее из k элемен- тов. Размещениями являются комбинации k элементов, взятых из данных n элементов, отличающиеся либо составом элементов, либо порядком их распо- ложения.

Число размещений из n	элементов по k			элементов обозначается A k	и
				n
вычисляется по формуле
A k	= n(n -1)(n - 2) ×...× (n - k +1)
n
или
A k =		n!		A 0 =1.
			,
	n	(n - k )!		n

92

Пример 10.1. Сколько различных размещений по 2 элемента можно со- ставить из элементов множества M = {x, y, z}?

Из трех элементов множества M можно составить следующие различные размещения по 2 элемента: (x, y) , (x, z) , ( y, x) , ( y, z) , (z, x) , (z, y) . Их число

A 2	= 3 × 2 = 6 .
3

Перестановкой из n элементов называется размещение из n элементов по n элементов. Перестановками являются комбинации данных n элементов, отличающиеся друг от друга только порядком расположения элементов.

Число перестановок из n элементов обозначается Pn и вычисляется по формуле

Pn = n!.

Пример 10.2. Сколько различных перестановок можно составить из эле- ментов множества M = {x, y, z}?

Из элементов множества M можно составить следующие перестановки

элементов: (x, y, z) , (x, z, y) , ( y, x, z) , ( y, z, x) ,	(z, x, y) , (z, y, x) . Их число
P3 = 3! =1× 2 ×3 = 6 .

Сочетанием из n элементов по k элементов ( 0 < k ≤ n ) называется любое подмножество данного множества, состоящее из k элементов. Сочетаниями яв- ляются комбинации k элементов, взятых из данных n элементов, отличающие- ся составом элементов.

Число сочетаний из n элементов по k элементов обозначается C k							и вы-
						n
числяется по формуле:
	Cn k =	n(n -1)(n - 2) ×...× (n - k +1)
			1× 2 ×3 ×...× k
	Cn k =		n!		=1.
или				, Cn0
			k !(n - k )!

Пример 10.3. Сколько различных сочетаний по 2 элемента можно соста- вить из элементов множества M = {x, y, z}?

Из трех элементов множества M можно составить следующие различные

сочетания по 2 элемента: (x, y) , (x, z) , ( y, z) . Их число C 2	=	3!		=	3 × 2	= 3.
3	2!×1!			2

Число Cn k обладает следующими свойствами:

1)Cn k = Cn n−k ;

2)	C k + C k +1		= C k +1 ;
	n	n	n+1
			n
3)	(a + b)n = ∑Cnk ak bn−k для любых a,b , n (бином Ньютона).

k =0

93

	Пример 10.4. Записать комплексное число (2 + i)4	в алгебраической фор-
ме.
	Используя свойство 3) получим:
	4
	(2 + i)4 = (i + 2)4 = ∑C4k ik 2n−k = C40i0 24 + C41i1 23 + C42i2 22 + C43i3 21 + C44i4 20 =
	k =0
	= 16 + 32i − 24 − 8i + 1 = −7 + 24i .

Схема выбора с возвращением

Если при выборке k элементов из n элементы возвращаются обратно и упорядочиваются, то получившиеся комбинации элементов называются разме- щениями с повторениями. Размещениями с повторениями являются комбина- ции k элементов, взятых из данных n элементов, отличающиеся либо составом элементов, либо порядком их расположения, либо количеством повторений элементов.

Число размещений с повторениями из n элементов по k элементов обо-

k

значается An и вычисляется по формуле:

Akn = nk .

Пример 10.5. Сколько различных размещений по 2 элемента с повторе- ниями можно составить из элементов множества M = {x, y, z}?

Из трех элементов множества M можно составить следующие различные

размещения по 2 элемента с повторениями: (x, x) , (x, y) , (x, z) , ( y, x) , ( y, y) ,

( y, z) , (z, x) , (z, y) , (z, z) . Их число A32 = 32 = 9 .

Если при выборке k элементов из n элементы возвращаются об- ратно без последующего упорядочивания, то получившиеся комбинации эле-

ментов называются сочетаниями с повторениями.

Число сочетаний с повторениями из n элементов по k элементов

k

обозначается C n и вычисляется по формуле:

C kn = C k+ − . n k 1

Пример 10.6. Сколько различных сочетаний по 2 элемента с повторения- ми можно составить из элементов множества M = {x, y, z}?

Из трех элементов множества M можно составить следующие различные

сочетания по 2 элемента с повторениями: (x, x) , (x, y) , (x, z) , ( y, y) , ( y, z) ,

	(z, z) . Их число		32 = C 2	=		4!	= 6 .
		C
	4			2!2!
	Пусть в множестве с n элементами есть k различных элементов, 1-й эле-
	мент повторяется n1 раз,					2-й - n2 раз, …,		k -й элемент - nk раз, причем
	n1 + n2 + ... + nk = n .

Перестановки из n элементов данного множества называются пере-

становками с повторениями из n элементов.

Число перестановок с повторениями из n элементов обозначается Pn (n1, n2 ,..., nk ) и вычисляется по формуле

94

	Pn (n1, n2 ,..., nk ) =	n!
			.
		n1 !n2 !...nk !
	Пример 10.7. Сколько различных перестановок можно составить из букв
слова «водопад»?
	В слове «водопад» 7 букв, из них одна буква «в», две буквы «о», две бук-

вы «д», одна – « а» и одна «п», следовательно, число различных перестановок

этих букв равно P7 (1, 2, 2,1,1) =

7!

=1260 .

1!× 2!× 2!×1!×1!

Формула включений и исключений

Пусть имеются N предметов, каждый из которых обладает, либо не об-

ладает свойством P ,

P ,…,

P .

Обозначим через N (P , P ,..., P )

количество

1

2

n

1 2

k

предметов, обладающих свойствами

P ,

P ,…,

P (и, быть может,

некоторыми

1

2

k

другими). Тогда число N (

P

,

P

,...,

P

)

предметов, не обладающих ни одним из

1

2

n

указанных свойств, определяется по следующей формуле:

N (

P

,

P

,...,

P

) = N - N (P ) - N (P ) - ... - N (P ) + N (P , P ) + N (P , P ) + ...

1 2

n

1

2

n

1 2

1 3

+N(P, P ) +... + N(P

, P ) - N(P, P , P ) -... - N (P

, P

, P ) + ... + (-1)n N(P, P ,..., P ) .

1 n

n−1

n

1 2 3

n−2

n−1

n

1 2

n

	Пример 10.8. Сколько положительных чисел от 1 до 100 не делится ни на
одно из чисел 2, 3, или 5?
	Обозначим через P свойство числа делиться на 2, через P свойство де-
				1										2
лимости на 3, через P3 свойство делимости на 5.
	Чтобы найти, сколько чисел от 1 до N делится на n надо разделить N на
n и взять целую часть получившегося частного, следовательно,
						N (P ) = 50 , N (P ) = 33 , N (P ) = 20 ,
						1				2		3
	N (P , P ) = 16 , N (P , P ) = 10 , N (P , P ) = 6 , N (P , P , P ) = 3 .
	1	2				1			3	2	3	1	2	3
По формуле включений и исключений получим:
	N (			,		,		) =100 - 50 - 33 - 20 +16 +10 + 6 - 3 = 26 .
			P		P		P
		1		2		3

А) Контрольные вопросы

10.1 Вычислите:

а) A 3

;

б) P ;

в) C 3

;

3

;

3

;

е) P (2, 2,1) .

г) A5

д) C5

5

5

5

5

10.2Докажите формулы:

а) Cn k = Cn n−k ;

б)	C k + C k +1		= C k +1 ;
	n	n	n+1
	n
в)	∑Cn k = 2n .

k =0

95

Б) Задачи и упражнения

10.3Из города А в город В ведут 3 дороги, а из города В в город С ведут 5 до- рог. Сколькими способами можно попасть из города А в город С через город В?

10.4Группа студентов изучает 8 дисциплин. Сколькими способами можно со- ставить расписание занятий в среду, если в этот день должно быть 3 раз- личных занятия; не более 3 различных занятий?

10.5Сколькими способами можно составить трехцветный полосатый флаг, ес- ли имеется материал 5 различных цветов? Тот же вопрос, при условии, что одна полоса обязательно должна быть белой?

10.6Из состава конференции, на которой присутствует 32 человека, нужно избрать делегацию, в составе 3 человек. Сколькими способами можно это сделать?

10.7На собрании присутствует 25 человек. Им нужно избрать председателя собрания, заместителя председателя и секретаря. Сколькими способами можно это сделать?

10.8Сколько различных семизначных чисел можно записать, используя циф-

ры 3, 5, 7?

10.9Сколько различных перестановок образуется из следующих слов:

а) океан; б) озеро; в) оборона; г) барабан?

10.10У бабушки 2 яблока, 2 банана и 3 апельсина. Каждый день в течение не- дели она выдает внуку по одному фрукту. Сколькими способами она мо- жет это сделать?

10.11В группе обучаются 25 студентов. После сдачи экзаменационной сессии 4 студента имеют задолженность только по математическому анализу, 4 – только по физике и 3 – только по дискретной математике. И математиче- ский анализ и физику нужно пересдавать 3 студентам, математический анализ и дискретную математику – 2 студентам, физику и дискретную математику – 2 студентам. Один студент в группе имеет долг по всем этим предметам. Скольким студентам пересдачи по этим предметам не потребовались?

В) Тестовые задания (укажите единственный верный ответ)

10.12 Значение выражения					A3	+ A5	равно…
					10	10
						A7
						10
а)		31	;
	10
б)		1		;

20

в) 43 ; 840

г) 882.

96

	10.13 Значение выражения	C3	×C5	равно…
		10	10
		C8
			10

а) 1 ; 90

б) 672 ; в) 90; г) 56.

10.14Из 10 студентов первого курса, 12 студентов второго курса и 8 студентов третьего курса нужно сформировать команду для участия в олимпиаде, состоящую из 3 человек. Известно, что в команду должен входить пред- ставитель каждого курса. Число способов, которыми можно сформиро-

вать команду равно…

а) 30; б) 1080; в) 960; г) 56.

10.15У одного человека есть 5 книг по математике, а у другого – 7. Число спо- собов, которыми они могут обменять две книги одного на две книги дру-

гого равно…

а) 31; б) 210; в) 2580;

г) 91200.

10.16На железнодорожной станции 6 светофоров. Каждый светофор имеет 3 состояния: красный, желтый, зеленый Число различных сигналов, кото-

рые могут быть поданы, равно…

а) 9; б) 18; в) 216; г) 729.

10.17Число различных перестановок, образованных из слова «поход», равно…

а) 5; б) 6; в) 60; г) 120.

10.18Из группы, состоящей из 5 мужчин и 4 женщин надо выбрать 5 человек так, чтобы среди них было не менее 2 женщин. Число способов, которы-

ми можно сделать такой выбор, равно…

а) 14; б) 60; в) 105; г) 96.

97

равна…

Варианты тестовых заданий

			Вариант 1
1..	Дано множество N10		= {1,2,3,4,5,6,7,8,9,10} и два его подмножества
	А={a | a N10 , а –		четное}, В={b | b N10 , b ³ 5 }.
	Множество A Ç		равно…
		B
	а) {1,3,5,6,7,8,9,10} ;		б) {2, 4} ;
	в) {5,7,9};		г) {1,3,6,8,10} .
2.	Даны произвольные множества А, В, С. Множеству ( A Ç B) È C соответст-
	вует диаграмма Эйлера…
	а)		б)

в)

г)

3. Дано бинарное отношение R={(x,y) | x,y {1,2,3,4,5,6,7,8}, x>y}.

Область значений отношения R−1

а)	{1,2,3,4,5,6,7};	б)	{1,2,3,4,5,6,7,8};
в)	{2,3,4,5,6,7,8};	в)	{2,3,4,5,6,7}.

4.Бинарное отношение R={(x,y) | x,y {1,2,3,4,5,6,7,8}, x+y>10} является…

а) рефлексивным, симметричным и транзитивным;

98

б) нерефлексивным, несимметричным и нетранзитивным; в) нерефлексивным, симметричным и нетранзитивным; г) антирефлексивным, антисимметричным и транзитивным.

5.Разностью A \ B множеств A и B называется множество…

	а) {x | (x A) (x B)};				б)	{x | (x A) (x B)};
	в) {x | (x A) & (x B)};				г)	{x | (x A) & (x B)}.
6.	Отношение		f из A в B называется функциональным, если оно обладает
следующим свойством…
	а)	если	f (a) = b и	f (a) = c , то b = c ;
	б)	если	f (a) = b и	f (c) = b , то a = c ;
	в) область определения Dom( f ) = A;
	г)	область значений Im( f ) = B .

7. Формула ( y → x) (x → y) является…

а) тождественно истинной; б) тождественно ложной; в) выполнимой; г) неизвестно какой.

8. Функция x yz xyz xz существенно зависит…

а) от переменных x и z ;

б)

от переменных x и y ;

в) от переменной x ;

г)

от переменной z .

9. Двойственной к функции

(xy

)(x

)

является функция…

z

y

x

y

z

а) x y z ;

б)

;

x

y

z

в) xyz ;

г)

.

x

y

z

10.СДНФ функции f = (10100110)T имеет вид…

а) x y z xy z x yz xy z ;

б) x yz xyz x y z xyz ;

в) (x y z )(x y z)(x y z)(x y z ) ; г) (x y z )(x y z)(x y z)( x y z ) .

99

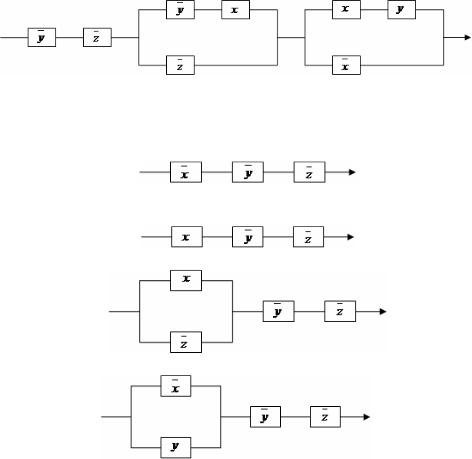
11.Дана релейно-контактная схема

Схема, эквивалентная данной, имеет вид…

а)

б)

в)

г)

12.Не является линейной логическая функция…

а) x Å y ;

б)

x y ;

в)

x

; г)

x y .

13.Дана программа машины Тьюринга

q10 q21R; T = q11 q10R;q2 0 q11R;q21 q01E.

и начальная конфигурация	P = q10000101. Заключительная конфигу-
рация T ( P) имеет вид…
а) 111101q01;	б) 111111q01;
в) 111101q0 0 ;	г) 111100q01.

100