ДМ Практикум

в) «Многочленом Жегалкина представима любая логическая функция, кроме константы 1»;

г) «Многочленом Жегалкина представима любая логическая функция, кроме константы 0»;

4.40Классу линейных функций принадлежит функция…

а) (x Å y)x ;

б) (x Å y) y ;

в) (x Å y) Å xy ;

г) (x Å y) Å x .

4.41Классу функций, сохраняющих 0, не принадлежит функция…

а) (x Å y)x ;

б) (x Å y) y ;

в) (x Å y) Å xy ;

г) (x Å y) Å x .

4.42Монотонной является функция…

а) x Å y ;

б) x → y ;

в) x y ;

г) x y .

41

Глава V. Предикаты

Предикатом P(x1 , x2 ,..., xn ) называется функция типа P : M1 ×M 2 ...×M n →B , где M i – произвольное множество, а В={0,1}. M i называется предметной обла-

стью предиката, xi (i=1,2,..,n) – предметными переменными. Предикат от n пе-

ременных называется n-местным.

Областью истинности предиката P(x1 , x2 ,..., xn ) называется множество

IP M1 ×M 2 ×...×M n , на котором P(x1 , x2 ,..., xn ) = 1.

Пусть P(x) предикат, определенный на множестве М. Высказывание “ для всех x из М P(x) истинно” обозначается xP(x) , при этом знак x называется квантором общности. Высказывание “ существует x из М такой, что P(x) ис- тинно” обозначается xP(x) , при этом знак x называется квантором сущест-

вования.

Переменная, на которую навешен квантор, называется связанной. Несвя- занная квантором переменная называется свободной. Выражение, на которое навешен квантор, называется областью действия квантора. Все вхождения пе- ременной x в это выражение являются связанными.

Из предикатов как высказываний можно образовывать составные выска-

зывания – формулы логики предикатов.

Формула F (x1, x2 ,..., xn ) называется выполнимой в области М, если в об- ласти М для формулы F существует такая подстановка констант a1, a2 ,..., an вместо переменных x1, x2 ,..., xn , что F (a1, a2 ,..., an ) становится истинным выска- зыванием. Формула F называется выполнимой, если существует область М, где F выполнима.

Формула F (x1, x2 ,..., xn ) называется тождественно истинной в области М, если F выполнима в М при любых подстановках констант. Формула F на-

зывается тождественно истинной или общезначимой, если она тождественно истинна в любых М.

Формула F (x1, x2 ,..., xn ) называется тождественно ложной в области М,

если F невыполнима в М. Формула F называется тождественно ложной или противоречивой, если она невыполнима ни в каких М.

В логике (алгебре) предикатов справедливы все эквивалентные соотно- шения логики (алгебры) высказываний, а также собственные эквивалентные соотношения, включающие кванторы x и x :

1.xP(x) ~ xP(x) ;

2.xP(x) ~ xP(x) ;

3.x yP(x, y) ~ y xP(x, y) ;

42

4.x yP(x, y) ~ y xP(x, y) ;

5.( xP(x) & xQ(x)) ~ x(P(x) & Q(x)) ;

6.( xP(x) xQ(x)) ~ x(P(x) Q(x)) ;

7.x(P(x) & Q( y)) ~ ( xP(x) & Q( y)) ;

8.x(P(x) Q( y)) ~ ( xP(x) Q( y)) ;

9.x(P(x) & Q( y)) ~ ( xP(x) & Q( y)) ;

10.x(P(x) Q( y)) ~ ( xP(x) Q( y)) .

Для всякой формулы F существует эквивалентная ей префиксная нор- мальная форма (ПНФ), имеющая вид:

Q1x1Q2 x2 ...Qn xn F′ ,

где Q1x1Q2 x2 ...Qn xn - кванторы; F′ - формула, не содержащая кванторов, с опе- рациями {&, ,¬}.

Пример 5.1 Привести к ПНФ предикатную формулу:

x yP(x, y) & x yQ(x, y) .

Вначале переместим отрицание непосредственно к символам предикатов,

для чего применим к исходной формуле правило де Моргана относительно &, а затем соотношения 1. и 2.:

x yP(x, y) & x yQ(x, y)

x yP(x, y) x yQ(x, y)

x yP(x, y) x yQ(x, y)

x yP(x, y) x yQ(x, y) .

Квантор всеобщности x не дистрибутивен относительно дизъюнкции, поэтому далее поменяем во втором предикате переменную x на z , дважды применим соотношение 8., затем соотношение 6.:

x yP(x, y)

x yQ(x, y) x yP(x, y) z yQ(z, y)

x( yP(x, y)

z yQ(z, y)) x z( yP(x, y) yQ(z, y))

x z y(

P(x, y)

Q(z, y)) .

Формулировки многих математических теорем могут быть записаны в

виде предикатной формулы x(P(x) → Q(x)) ,

x M , где предикат P(x) являет-

ся условием данной теоремы, а предикат Q(x)

- заключением данной теоремы.

Теоремы, отличающиеся друг от друга условием или заключением, являются

различными теоремами.

43

Если теорема x(P(x) → Q(x)) ,	x M	верна, то предикат P(x) является
достаточным условием для Q(x) ,	а предикат Q(x) является необходимым ус-
ловием для P(x) .
Всякая теорема x(P(x) → Q(x)) , x M		(прямая теорема) порождает еще
три теоремы:

∙обратную x(Q(x) → P(x)) , x M ;

∙противоположную x(P(x) → Q(x)) , x M ;

∙противоположную обратной x(Q(x) → P(x)) , x M .

Прямая теорема и теорема противоположная обратной либо обе истинны, либо обе ложны, т. е. имеет место эквивалентность:

x(P(x) → Q(x)) x(Q(x) → P(x)) , x M .

На этом эквивалентном соотношении основан метод доказательства от противного, который состоит в том, что вместо доказательства прямой теоремы проводят доказательство теоремы, противоположной обратной.

Пример 5.2. Для верной теоремы «Если функция y = f (x) дифференци- руема в некоторой точке x = x0 , то она непрерывна в этой точке» сформулируем обратную, противоположную и противоположную обратной теоремы.

1) обратная теорема: «Если функция y = f (x) непрерывна в некоторой точке

x= x0 , то она дифференцируема в этой точке» (теорема неверна);

2)противоположная теорема: «Если функция y = f (x) не дифференцируема в некоторой точке x = x0 , то она не является непрерывной в этой точке» (теорема неверна);

3)теорема, противоположная обратной: «Если функция y = f (x) не является непрерывной в некоторой точке x = x0 , то она не дифференцируема в этой

точке» (теорема верна).

44

А) Контрольные вопросы

5.1Пусть Q : 2 → B предикат порядка, такой что Q(a1 , a2 ) = 1 a1 < a2 .

Какие из следующих высказываний являются истинными, какие – лож- ными, а какие – переменными?

а) Q(2,3);	б) Q(3,2);
в) Q(x,2);	г) Q(2,x);	д) Q(x,y).

5.2Используя предикат Q из 5.1, запишите логической формулой следующие высказывания:

а) для любого натурального числа найдется натуральное число, которое больше него;

б) существует натуральное число, меньшее всех других натуральных чи- сел.

5.3 Пусть предикат D(x, y) - « x делится на y », определенный на множестве N натуральных чисел (без нуля). Рассмотрите все возможные варианты навешивания кванторов на данный предикат и определите истинность получившихся высказываний.

5.4Приведите пример выполнимой, тождественно истинной, тождественно ложной формулы логики предикатов.

5.5Какие из следующих шести теорем являются по отношению друг к другу обратными, противоположными, противоположными обратным? Какие из этих теорем верны?

а) Если каждое из двух натуральных чисел делится нацело на 5, то их сумма делится на 5.

б) Если ни одно из двух натуральных чисел не делится нацело на 5, то и их сумма не делится нацело на 5.

в) Если хотя бы одно из двух натуральных чисел делится на 5, то и их сумма делится на 5.

г) Если сумма двух натуральных чисел делится нацело на 5, то каждое слагаемое делится на 5.

д) Если сумма двух натуральных чисел не делится нацело на 5. то ни одно из слагаемых не делится на 5.

е) Если сумма двух натуральных чисел не делится нацело на 5, то хотя бы одно из слагаемых не делится на 5.

5.6Докажите эквивалентное соотношение:

x(P(x) → Q(x)) x(Q(x) → P(x)) , x M .

45

Б) Задачи и упражнения

5.7Выясните, истинны или ложны высказывания:

а) n б) n в) n г) n д) x

е) x

k n = 2k ;k n = 2k ;k n = 2k ;k n = 2k ;

y z x + y = z ;

k c kx2 + c2 > 0 .

5.8Пусть S предикат суммы, такой что S (a1, a2 , a3 ) = 1 a1 + a2 = a3 и E пре- дикат равенства, такой что E(a1, a2 ) = 1 a1 = a2 . Определите истинность, ложность либо выполнимость в области натуральных чисел следую- щих формул:

а) xS (x, x, y) ;

б) yS (x, x, y) ;

в) xS (x, y, y) → yS (x, y, y) ;

	г) (S (x, y, z) & S ( y, x,u)) → E(z,u) ;
	д) x y z u(S (x, y, z) & S (x, y,u)) → E(z,u)) .
5.9	Пусть P(x) - предикат « x − 3 > 0 » и Q(x) - предикат « x + 3 > 0 », x .
	Укажите область истинности формул:
	а) P(x) & Q(x) ;			б) P(x) Q(x) ;
	в) P(x) → Q(x) ;			г) Q(x) → P(x) ;
				е)		®		.
	д) P(x) &	Q(x)	;		Q(x)		P(x)
5.10	Найдите область истинности предиката:
	а) $x(x2 + y 2 £1) x, y ;
	б) "x(x2 + y 2 ³1) x, y ;
	в) $y(x2 + y2 >1) x, y ;
	г) "y(x2 + y2 <1) x, y ;
	д) $x( y > x2 ) Å ( y £1) , если x , y [−2,2] ;

е) ( y ≤ 5) ~"x( y > x2 ) , если x [−2,2],									y .
5.11 Найдите область истинности предиката:
а)	(	)	x	(	)	,	(	]	[	0,10	)	;
		y <5			y +3 >3x		x −∞, 2		, y

46

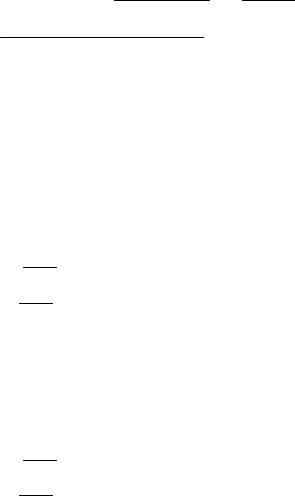
б)

(

y

≤8

)

(

y

+1

)

, x

(

]

[

)

→ x

> 2x

−∞,3 , y

0, 21 .

в) x

((

y

)

(

))

,

[

]

[

0, 7

]

.

> 2x +1

3x + y <1

x

−1,1 , y

г) x

((

y

> x + 2

)

&

(

))

[

−3, 4

]

, y

[

)

.

x + y ≥3

, x

0,∞

5.12Приведите к ПНФ предикатную формулу:

а) x yP(x, y) → x yQ(x, y) ;

б) ( x yP(x, y) xQ(x)) → y zR( y, z) ;

в) ( x zP(x, z) x yQ(x, y)) → zR(z) ;

г) x yP(x, y) x yQ(x, y) .

Тестовые задания (укажите единственный верный ответ)

В)

5.13Высказывание «для всех x из области определения P(x) истинно» обо- значается…

а) xP(x) ;

б) xP(x) ;

в) xP(x) ;

г) xP(x) .

5.14Высказывание «существует x из области определения такой, что P(x) ис- тинно» обозначается…

а) xP(x) ;

б) xP(x) ;

в) xP(x) ;

г) xP(x) .

5.15Пусть S : 3 → B предикат суммы, такой что S (a1, a2 , a3 ) = 1 a1 + a2 = a3 Истинным на множестве натуральных чисел является высказывание…

а) x yS (x, y,5) ;

б) x yS (x, y,5) ;

в) x yS (x, y,5) ;

г) x yS (x, y,5) .

47

5.16Пусть S : 3{0} →B предикат суммы, такой что S(a1,a2 ,a3 ) =1 a1 + a2 = a3 . Ложным на множестве натуральных чисел является высказывание…

а) x yS (x, y, y) ;

б) x yS (x, y, y) ;

в) x yS (x, y, y) ;

г) x yS (x, y, y) .

5.17Пусть P(x) - предикат « x2 > 9 » и Q(x) - предикат « x ≤ 5 », x . Область истинности формулы P(x) & Q(x) имеет вид…

а) x (3;5] ;

б) x (−∞;−3) (3;5] ;

в) x (−∞;5] ;

г) x (−∞; +∞) .

5.18Пусть P(x) - предикат « x2 > 9 » и Q(x) - предикат « x ≤ 5 », x . Область истинности формулы P(x) Q(x) имеет вид…

а) x (3;5] ;

б) x (−∞;−3) (3;5] ;

в) x (−∞;5] ;

г) x (−∞; +∞) .

5.19Область истинности предиката x(x2 + y > 3) , x, y имеет вид…

а) y (3;+∞) ;

б) y (−∞;0] ;

в) y (−∞;3];

г) y (−∞; +∞) .

5.20Префиксной нормальной формой (ПНФ) является формула…

а) x yP(x, y) x yQ(x, y) ;

б) x( y(P(x, y) Q(x, y))) ;

в) x z y(P(x, y) Q(z, y)) ;

г) x( y(P(x, y) yQ(x, y)) .

48

5.21Префиксная нормальная форма формулы x yP(x, y) x yQ(x, y) имеет вид…

а) x y(P(x, y) & Q(x, y)) ;

б) x y(P(x, y) Q(x, y)) ;

в) x y z(P(x, y) Q(x, z)) ;

г) x y z(P(x, y) & Q(x, z)) .

49

Глава VI. Машины Тьюринга

Машина Тьюринга (МТ) – это воображаемое устройство для реализации алгоритмических процессов.

Определение МТ. Машина Тьюринга представляет собой тройку T = ( A,Q, P) , где A = {a0 , a1,..., an }- внешний алфавит с выделенным пустым сим- волом a0 ; Q = {q0 , q1,..., qk }- внутренний алфавит состояний управляющего уст- ройства ( q0 -заключительное состояние, q1 - начальное, остальные состояния – рабочие); P - программа, состоящая из команд типа qi am q j an S , S {R, L, E} (направо, налево, на месте).

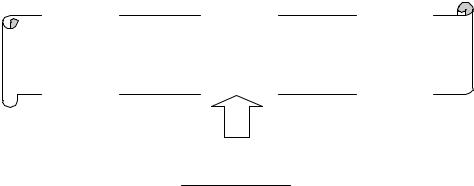
Устройство МТ. (Рисунок 6.1) В конструкцию машины входит бесконеч- ная в обе стороны лента (1), разбитая на ячейки. В начальный момент времени в конечном количестве ячеек записаны символы из A (по одному в каждой ячейке), в остальных – пустой символ. Машина содержит головку (2), которая в любой момент времени может обозревать некоторую ячейку, считывать сим- вол, записанный в ней, стирать этот символ и заносить на его место любой другой из A . Так же головка может передвигаться вдоль ленты влево и вправо (на одну ячейку за один шаг). Руководит работой МТ управляющее устройство (3), находящееся в одном из состояний qi Q , и действующее в соответствии с программой P .

		(1)	…			an			…	…
						(2)
				(3)		q
						j
			Рисунок 6.1
Шаг работы МТ. Если управляющее устройство МТ находится в состоя-
нии qi , в обозреваемой ячейке записан символ am									и в программе присутствует

команда qi am q j an S , то головка МТ стирает символ am , записывает на его ме-

сто an , передвигается в зависимости от символа S и переходит в состояние q j .

В начальный момент времени МТ находится в состоянии q1 . МТ прекращает работу, если переходит в состояние q0 или получает команду, не предусмот- ренную программой.

Конфигурацией (машинным словом) называется совокупность UqiV , где

U и V наборы символов (слова) из алфавита A . U - слово левее головки, V - слово правее головки (включая символ под головкой). qi - состояние МТ.

50