
- •Эконометрика оглавление
- •1.Общие методические указания к изучению дисцпилины
- •2.Основные темы курса
- •Тема 1. Задачи эконометрики в области социально-экономических исследований. Основные этапы эконометрического моделирования.
- •Тема 2. Классическая и обобщенная линейные модели
- •Тема 3. Линейные регрессионные
- •Тема 4. Нелинейные модели регрессии и их линеаризаци.
- •Тема 5. Эконометрическое моделирование временных рядов
- •Примерный перечень вопросов к зачету по дисциплине «Эконометрика»
- •Рекомендуемая литература Основная
- •Дополнительная
Тема 2. Классическая и обобщенная линейные модели
множественной регрессии
Экономические явления определяются, как правило, большим числом совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной переменной Y от нескольких объясняющих переменных X1,Х2,…Хn. Эта задача решается с помощью множественного регрессионного анализа.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели, включающего отбор факторов и выбор вида уравнения регрессии. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
они должны быть количественно измеримы (качественным факторам необходимо придать количественную определенность);
между факторами не должно быть высокой корреляционной, а тем более функциональной зависимости, т.е. наличия мультиколлинеарности.
Включение в модель мультиколлинеарных факторов может привести к следующим последствиям:
Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом виде», поскольку факторы связаны между собой; параметры линейной регрессии теряют экономический смысл;
Оценки параметров ненадежны, имеют большие стандартные ошибки и меняются с изменением объема наблюдений.
Пусть
![]() - матрица – столбец значений зависимой
переменной размераn;
- матрица – столбец значений зависимой
переменной размераn;
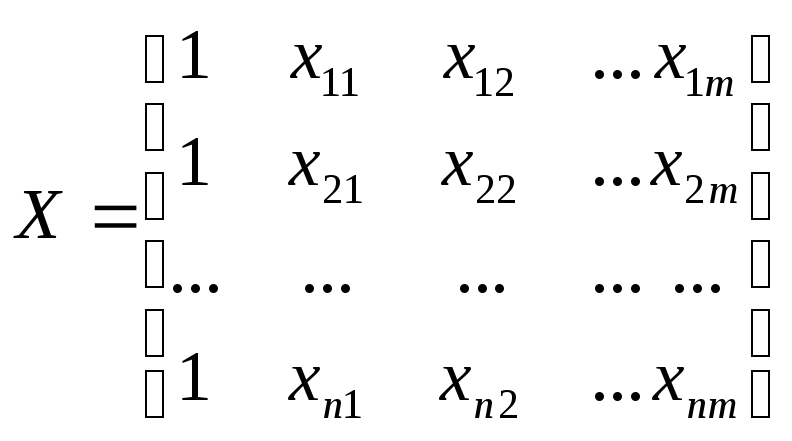 -
матрица значений, объясняющих переменных;
-
матрица значений, объясняющих переменных;
![]() -
матрица – столбец (вектор) параметров
размера m+1;
-
матрица – столбец (вектор) параметров
размера m+1;
![]() -
матрица – столбец (вектор) остатков
размера n.
-
матрица – столбец (вектор) остатков
размера n.
Тогда в матричной форме модель множественной линейной регрессии запишется следующим образом:
![]() (1)
(1)
При оценке параметров уравнения регрессии (вектора b) применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки.
В модели (1) ε – случайный вектор, Х - неслучайная (детерминированная) матрица.
Математическое ожидание величины остатков равно нулю: М(ε) = 0n.
Дисперсия остатков εi постоянна для любого i (условие гомоскедастичности), остатки εi и εj при i≠j не коррелированны:
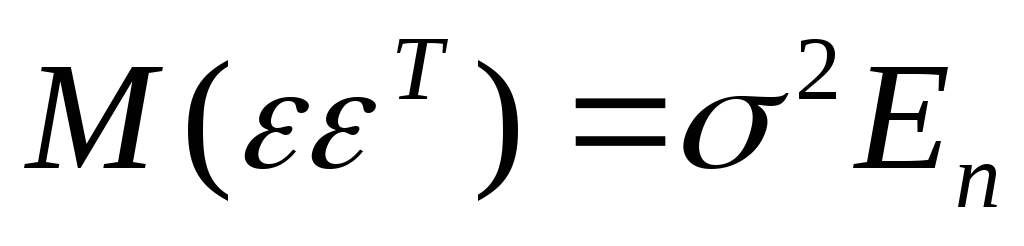 .
.ε – нормально распределенный случайный вектор, т.е. ε~N(0n;σ2 En).
r(X)=m+1<n. Столбцы матрицы Х должны быть линейно независимыми (ранг матрицы Х максимальный, а число наблюдений n превосходит ранг матрицы).
Модель (1), в которой зависимая переменная, остатки и объясняющие переменные удовлетворяют предпосылкам 1-5 называется классической нормальной линейной моделью множественной регрессии (КНЛММР). Если не выполняется только предпосылка 4, то модель называется классической линейной моделью множественной регрессии (КЛММР).
Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений фактических значений от значений, найденных по уравнению регрессии, была минимальной:
![]()
Решением
этой задачи является вектор
![]()
Одной из наиболее эффективных оценок адекватности модели является коэффициент детерминации R2, определяемый формулой:
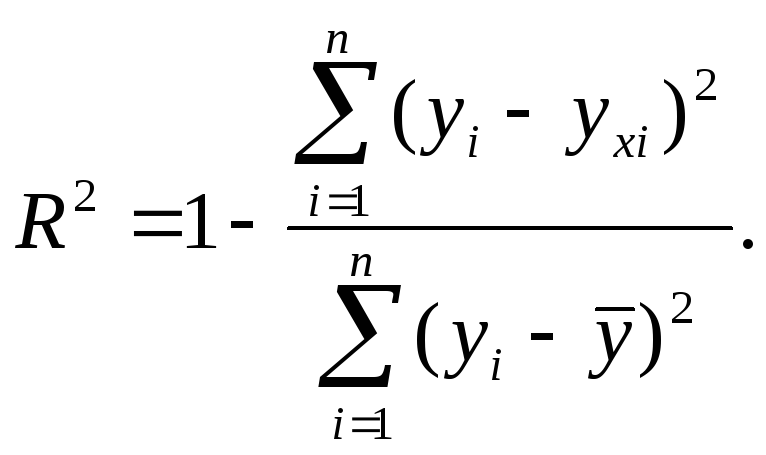
Коэффициент детерминации характеризует долю вариации зависимой переменной, обусловленной регрессией или изменчивостью объясняющих переменных. Чем ближе R2 к единице, тем лучше построенная регрессионная модель описывает зависимость между объясняющими и зависимой переменной.
Следует иметь в виду, что при включении в модель новой объясняющей переменной, коэффициент детерминации увеличивается, хотя это и не обязательно означает улучшение качества регрессионной модели. В этой связи лучше использовать скорректированный (поправленный) коэффициент детерминации R2, пересчитываемый по формуле:
![]()
где n – число наблюдений,
m – число параметров при переменных х.
Из
формулы следует, что с включением в
модель дополнительных переменных
разница между значениями
![]() и
и![]() увеличивается. Таким образом,
скорректированный коэффициент
детерминации может уменьшаться при
добавлении в модель новой объясняющей
переменной, не оказывающей существенного
влияния на результативный признак.
увеличивается. Таким образом,
скорректированный коэффициент
детерминации может уменьшаться при
добавлении в модель новой объясняющей
переменной, не оказывающей существенного
влияния на результативный признак.
Но использование только коэффициента детерминации для выбора наибольшего уравнения регрессии может оказаться недостаточным.
Средняя относительная ошибка аппроксимации рассчитывается по формуле:
![]()
Значимость уравнения регрессии в целом сводиться к проверке гипотезы об одновременном равенстве нулю всех коэффициентов регрессии при факторных признаках т.е. гипотезы:
![]()
Если данная гипотеза не отклоняется, то делается вывод о том, что совокупное влияние всех факторных признаков х1, х2, … хm , включенных в модель, на зависимую переменную y можно считать статистически несущественным. Проверка данной гипотезы осуществляется на основе дисперсионного анализа.
Основной идеей дисперсионного анализа является разложение общей суммы квадратов отклонений результативной переменной y от среднего значения y на «объясненную» и «остаточную»:

Для приведения дисперсий к сопоставимому виду, определяют дисперсии на одну степень свободы. Результаты вычислений заносят в специальную таблицу дисперсионного анализа.
Таблица 2.1.
Дисперсионный анализ
|
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Оценка дисперсии на одну степень свободы |
|
Общая |
|
m-1 |
|
|
Объясненная |
|
m |
|
|
Остаточная |
|
n-m-1 |
|
В данной таблице n – число наблюдений, m – число параметров при переменных х.
Сравнивая полученные оценки объясненной и остаточной дисперсии на одну степень свободы, определяют значение F – критерия Фишера, используемого для оценки значимости уравнения регрессии:
![]()
С помощью F – критерия проверяется нулевая гипотеза о равенстве дисперсий H0: SR2=S2.
Если нулевая гипотеза справедлива, то объясненная и остаточная дисперсии не отличаются друг от друга. Для того, чтобы уравнение регрессии было значимо в целом (гипотеза Н0 была опровергнута) необходимо, чтобы объясненная дисперсия превышала остаточную в несколько раз. Критическое значение F – критерия определяется по таблице Фишера – Снедекора.
Расчетное значение сравнивается с табличным, и если оно превышает табличное (Fрасч>Fтабл), то гипотеза Н0 отвергается, и уравнение регрессии признается значимым. Если Fрасч<Fтабл, то уравнение регрессии считается статистически незначимым. Нулевая гипотеза Но не может быть отклонена.
Расчетное значение F – критерия связано с коэффициентом детерминации R2 следующим соотношением:
![]()
где m –число параметров при переменных х;
n – число наблюдений.
Оценка значимости коэффициентов регрессии сводится к проверке гипотезы о равенстве нулю коэффициента регрессии при соответствующем факторном признаке, т.е. гипотезы:
Но : bi=0
Проверка гипотезы проводится с помощью t – критерия Стьюдента. Для этого расчетное значение t-критерия:
![]()
где bi – коэффициент регрессии при хi
mbi – средняя квадратическая ошибка коэффициента регрессии bi
сравнивается
с табличным tтабл
при заданном уровне значимости
![]() (для экономических процессов и явлений)
и числе степеней свободы (n-2).
(для экономических процессов и явлений)
и числе степеней свободы (n-2).
Если расчетное значение превышает табличное, то гипотезу о несущественности коэффициента регрессии можно отклонить.
Рассмотрим
интерпретацию параметров модели линейной
множественной регрессии. В линейной
модели множественной регрессии
![]() коэффициенты регрессииbi
характеризуют среднее изменение
результата с изменением соответствующего
фактора на единицу при неизменном
значении других факторов, закрепленных
на среднем уровне.
коэффициенты регрессииbi
характеризуют среднее изменение
результата с изменением соответствующего
фактора на единицу при неизменном
значении других факторов, закрепленных
на среднем уровне.
На практике часто бывает необходимо сравнить влияние на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии βi и коэффициенты эластичности Эi (i=1,2,…,m).
Уравнение регрессии в стандартизованной форме:
![]()
Где
![]() -
стандартизованные переменных.
-
стандартизованные переменных.
В
результате такого нормирования средние
значения всех стандартизованных
переменных равны нулю, а дисперсии равны
единице, т.е.
![]()
![]()
Коэффициенты
«чистой» регрессии связаны со
стандартизованными коэффициентами
следующим соотношением:
![]()
Стандартизованные коэффициенты показывают, на сколько стандартных отклонений (сигм) изменится в среднем результат, если соответствующий фактор х1 изменится на одно стандартное отклонение (одну сигму) при неизменном среднем уровне других факторов. Сравнивая стандартизованные коэффициенты друг с другом, можно ранжировать факторы по силе их воздействия на результат.
Средние коэффициенты эластичности вычисляются по формуле:
![]()
Коэффициент эластичности показывает, на сколько процентов (от средней) изменится в среднем Y при увеличении только фактора Xi на 1%.
При эконометрическом моделировании реальных экономических процессов предпосылки КЛММР нередко оказываются нарушенными: дисперсии остатков модели не одинаковы (гетероскедастичность остатков), или наблюдается корреляция между остатками в разные моменты времени (автокоррелированные остатки). Тогда предпосылка «3» запишется следующим образом:
![]() где
Ώ – положительно определенная матрица.
где
Ώ – положительно определенная матрица.
Принимая, что дисперсия объясняющих переменных могут быть произвольными, мы получаем обобщенную линейную модель множественной регрессии (ОЛММР).
В этом случае оценка параметров модели осуществляется обобщенным методом наименьших квадратов (ОМНК):
![]()
Если модель гетероскедастична, то матрица Ώ – диагональная. Тогда имеем:
![]()
В этом случае обобщенный метод наименьших квадратов называется взвешенным методом наименьших квадратов, поскольку мы «взвешиваем» каждое наблюдение с помощью коэффициента 1/σi.
На практике, однако, значения σi почти никогда не бывают известны. Поэтому сначала находят оценку вектора параметров обычным методом наименьших квадратов. Затем находят регрессию квадратов остатков на квадратичные функции объясняющих переменных, т.о. уравнение
![]()
Где f(x) – квадратичная функция.
Далее
по полученном уравнению рассчитывают
теоретические значения
![]() и определяют набор весов
и определяют набор весов![]() Затем
вводят новые переменных
Затем
вводят новые переменных![]() и находят уравнение
и находят уравнение![]() .
Полученная оценка и есть оценка
взвешенного метода наименьших квадратов.
.
Полученная оценка и есть оценка
взвешенного метода наименьших квадратов.
Проверить модель на гетероскедастичность можно с помощью следующих тестов: ранговой корреляции Спирмена; Голдфельда-Квандта; Уайта; Глейзера.
Рассмотрим тест на гетероскедастичность, применяемый в случае, если ошибки регрессии можно считать нормально распределенными случайными величинами, - тест Голдфельда-Квандта.
Все n наблюдений упорядочиваются в порядке возрастания значений фактора Х. затем выбираются m первых и m последних наблюдений.
Гипотеза о гомоскедастичности равносильна тому, что значения остатков e1,…,em и en-m+l,…,en представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии.
Гипотеза о равенстве дисперсий двух нормально распределенных совокупностей проверяется с помощью F – критерия Фишера.
Расчетное значение вычисляется по формуле (в числителе всегда большая сумма квадратов):
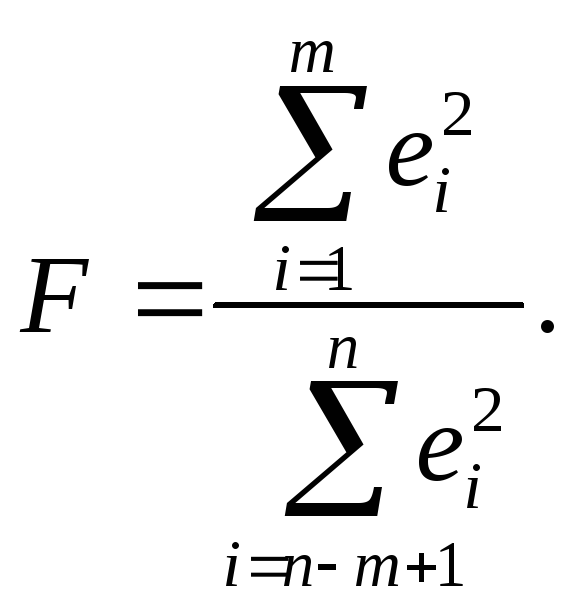
Гипотеза о равенстве дисперсий двух наборов по m наблюдений (т.е. гипотеза об отсутствии гетероскедастичности остатков) отвергается, если расчетное значение превышает табличное F>Fα;m-p;m-p, где p – число регрессоров.
Мощность теста (вероятность отвергнуть гипотезу об отсутствии гетероскедастичности, когда гетероскедастичности действительно нет) максимальна, если выбирать m порядка n/3.
Тест Голдфельда – Квандта позволяет выявить факт наличия гетероскедастичности, но не позволяет описать характер зависимостей дисперсий ошибок регрессии количественно.
Если прослеживается влияние результатов предыдущих наблюдений на результаты последующих, случайные величины (ошибки) εi в регрессионной модели не оказываются независимыми. Такие модели называются моделями с наличием автокорреляции.
Как правило, если автокорреляция присутствует, то наибольшее влияние на последующее наблюдение оказывает результат предыдущего наблюдения. Наличие автокорреляции между соседними уровнями ряда можно определить с помощью теста Дарбина-Уотсона. Расчетное значение определяется по следующей формуле:
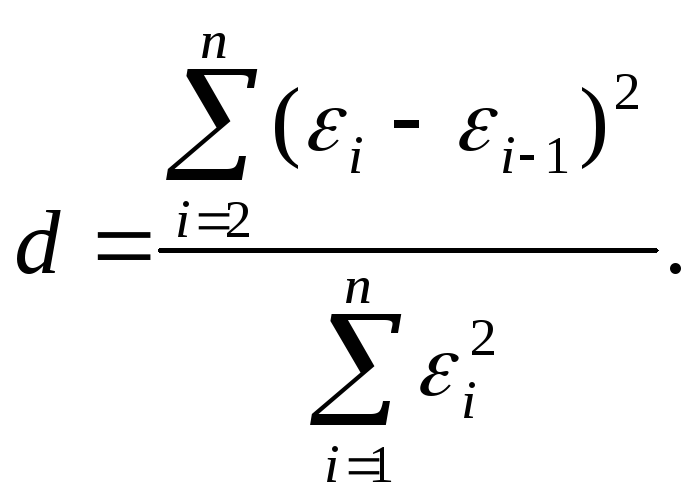
Значения
критерия находятся в интервале от 0 до
4. По таблицам критических точек
распределения Дарбина-Уотсона для
заданного уровня значимости
![]() ,
числа наблюдений (n)
и количества объясняющих переменных
(m)
находят пороговые значения dн
(нижняя
граница) и
dв
(верхняя
граница).
,
числа наблюдений (n)
и количества объясняющих переменных
(m)
находят пороговые значения dн
(нижняя
граница) и
dв
(верхняя
граница).
Если расчетное значение:
![]() ,
то гипотеза об отсутствии автокорреляции
не отвергается (принимается);
,
то гипотеза об отсутствии автокорреляции
не отвергается (принимается);
![]() или
или
![]() ,
то вопрос об отвержении или принятии
гипотезы остается открытым (расчетное
значение попадает в зону неопределенности);
,
то вопрос об отвержении или принятии
гипотезы остается открытым (расчетное
значение попадает в зону неопределенности);
![]() ,
то принимается альтернативная гипотеза
о наличии положительной автокорреляции;
,
то принимается альтернативная гипотеза
о наличии положительной автокорреляции;
![]() ,
то принимается альтернативная гипотеза
о наличии отрицательной автокорреляции.
,
то принимается альтернативная гипотеза
о наличии отрицательной автокорреляции.
Таблица 2.2.
Промежутки внутри интервала [0 - 4]
|
|
|
|
|
|
|
принимается альтернативная гипотеза о наличии положительной автокорреляции |
вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности) |
гипотеза об отсутствии автокорреляции не отвергается (принимается) |
вопрос об отвержении или принятии гипотезы остается открытым (расчетное значение попадает в зону неопределенности) |
принимается альтернативная гипотеза о наличии отрицательной автокорреляции |
Недостаток теста Дарбина – Уотсона заключается прежде всего в том, что он содержит зоны неопределенности. Во-вторых, он позволяет выявить наличие автокорреляции только между соседними уровнями, тогда как автокорреляция может существовать и между более отдаленными наблюдениями. Поэтому наряду с тестом Дарбина-Уотсона для проверки наличия автокорреляции используются тест серий (Бреуша – Годфри),Q- тест Льюинга – Бокса и другие. Наиболее распространенным приемом устранения автокорреляции во временных рядах является построение авторегрессионных моделей.
