устойчивость

2.5. Действие распределенной продольной нагрузки

	Перейдем к случаю, когда продольная нагрузка
	распределена по длине стержня. Одним из примеров
	такого типа нагрузки является собственный вес стерж­
	ня: при расчете колонн в крупных сооружениях, дымо­
	вых труб и т. д. его необходимо учитывать. Обычно в
	этих случаях один из концов колонны (верхний) явля­
	ется свободным, а второй (нижний) - защемленным.
	Рассмотрим задачу об устойчивости такого стержня с
	постоянным по длине сечением сначала под действием
	только собственного веса, а затем - при совместном
	действии силы веса и других нагрузок.
	Примем систему координат по рис. 2.5.1. Обозна­
	чим силу веса, приходящуюся на единицу длины, через		Рис. 2.5.1. К задаче об
			устойчивости стержня
	р. В сечении х сжимающая сила равна	Рх = рх, а по­

	перечная сила	под влиянием
		собственного веса
		(2.5.1)
	Уравнение (1.1.6а) преобразуем к виду
		(2.5.2)
	подставляя (2.5.1), получим:
		(2.5.3)
	Введем обозначения
		(2.5.4)
	тогда придем к уравнению
		(2.5.5)

Это уравнение интегрируется в бесселевых функциях; решение имеет вид

(2.5.6)

Здесь 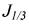- бесселева функция первого рода. Производная от функции по z равна

(2.5.7)

Основываясь на этой формуле, находим:

Дифференцируя (2.5.6), получаем:

Граничные условия задачи будут:

М =	при X = 0,

или
	при		при	(2.5.7а)
Как известно, функции		обращаются в нуль при		если индекс
если же	то функция		В нашем случае	следовательно, ве-
личина	в то время как		Но тогда первое из условий (2.5.7а)
может быть выполнено лишь при А = 0. Считая				из второго условия
находим:
				(2.5.8)
Наименьшее значение аргумента, при котором функция				обращается в нуль,
будет
				(2.5.8а)
По (2.5.4) находим:
				(2.5.9)

Введем понятие приведенной нагрузки, понимая под этим силу Р, сосредо­ точенную в известной точке и эквивалентную распределенной нагрузке в зада­ че устойчивости. Выберем центр приведения у свободного конца, тогда

и окончательно

(2.5.10)

Следовательно, приведенная сила составляет 1/3,18 часть от полного веса. Познакомимся с решением этой же задачи без непосредственного примене­

ния бесселевых функций, с помощью метода степенных рядов; этот метод широко применяется в аналогичных задачах.

Выпишем решение уравнения (2.5.5) в виде

(2.5.11)

Подставляя это выражение в (2.5.5), получим:

Сравнивая коэффициенты при одинаковых степенях, приходим к следующим соотношениям:

(2.5.13)

Таким образом, коэффициенты с индексами 2, 5, 8, 11 и т. д. обращаются в нуль:

при п=0, 1,2, ...

Остальные коэффициенты связаны зависимостью

Можно видеть, что все эти коэффициенты могут быть выражены через Со и С1:

Выражение для w принимает вид

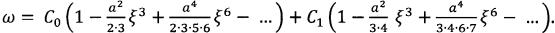(2.5.14) Производная по будет равна

(2.5.15)

Пользуясь первым из граничных условий (2.5.7а), находим С1 = 0. Второе из этих условий при 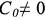приводит к уравнению

(2.5.16)

которое можно переписать в виде

(2.5.17)

В левой части этого уравнения содержится ряд, соответствующий бесселевой функции Таким образом, мы получили уравнение, эквивалентное (2.5.8); наименьший корень его определяется по (2.5.8а).

Реальные колонны больших размеров имеют, как правило, переменное сече­ ние. В этом случае непосредственное интегрирование уравнения упругой линии усложняется, и потому расчет на устойчивость необходимо проводить с помо­ щью приближенных методов. В качестве примера рассмотрим Останкинскую телевизионную башню в Москве высотой в 565 м. Определение коэффициента запаса устойчивости башни было выполнено с помощью метода последова­ тельных приближений; одновременно устанавливалась форма упругой линии. Далее определялись изгибающие моменты от вертикальных сил для ряда сече­ ний, и определялась новая упругая линия. Сравнение полученной стрелы про­ гиба с исходной давало возможность найти запас устойчивости.

2.6. Одновременное действие распределенной и сосредоточенной нагрузок

Перейдем к тому случаю, когда стержень подвер­ гается действию не только распределенной нагрузки р, но и сосредоточенной силы Р, приложенной к свобод­ ному концу (рис. 2.6.1). Для общности будем считать, что величина р является переменной: р = р(х). Вос­ пользуемся методом Бубнова-Галеркина; предвари­ тельно выведем исходное уравнение с учетом распре­ деленной нагрузки. Обратимся к вариационному урав­ нению, выведенному ранее. Выражение для вариации работы внутренних сил представим в виде (1.5.3а):

			(2.6.1)
	в отличие от 2.5 координата х отсчитывается от нижне­
	го конца стержня.
	Вычислим работу распределенной нагрузки, счи­
	тая ее интенсивность переменной по длине. На элемент
	dx приходится нагрузка р dx смещение		центра тяже­
Рис. 2.6.1. Одновременное	сти элемента по отношению к нижнему концу равно
действие сосредо­		dx.	(2.6.2)
точенной силы и собст­
венного веса для стержня	Полная работа распределенной нагрузки равна
с защемленным концом	W =	dx.	(2.6.3)
Введем обозначения	для результирующих нагрузки в пределах от 0
до х, от х до l и по всей длине:
			(2.6.4)

Интегрируя выражение (2.6.3) по частям, получим:

или

(2.6.5)

Окончательно

(2.6.6)

Вариация равна

(2.6.7)

Эту величину надо прибавить к выражению (1.5.10а); полная вариация работы внешних сил будет

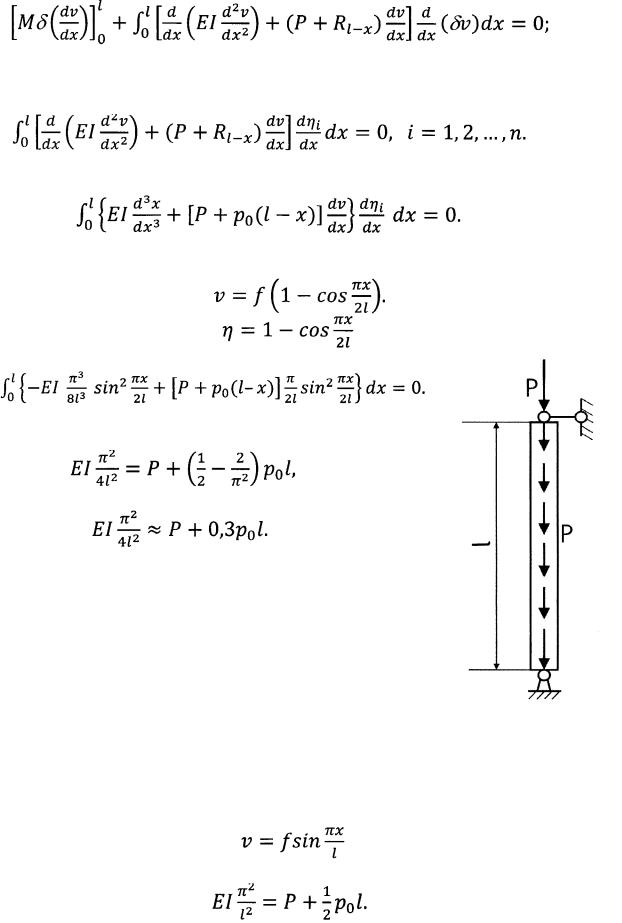
Вариационное уравнение можно представить в виде

жесткость EI здесь для общности принята переменной. Подставляя вместо выражение (1.8.1) и принимая внеинтегральный член равным нулю, получим основное уравнение метода Бубнова-Галеркина:

(2.6.10)

Рассмотрим случай, когда наряду с сосредоточенной силой Р должен быть уч­ тен собственный вес стержня р0l, причем EI = const. Вместо (2.6.10) получим:

(2.6.11)

Уравнение упругой линии примем в виде, соответствующем случаю одной со­ средоточенной силы:

Принимая

и подставляя два последних выражения в (2.6.11), находим;

(2.6.14)

Выполняя интегрирование, получаем:

(2.6.14)

или

(2.6.15)

Следовательно, расчет на продольный изгиб можно вести в рассматриваемом случае, присоединяя к сосре­ доточенной силе 3/10 от собственного веса стержня и счи­ тая эту приведенную нагрузку приложенной к свободному концу стержня. Если нагрузка р0 значительна, то при сум­ марной критической силе, равной (2.6.15), сила Р может получиться отрицательной, т. е. растягивающей. Получен­ ный нами результат хорошо согласуется с решением зада­ чи в бесселевых функциях, так как по (2.5.10) при Р = 0 мы получили приведенную нагрузку равной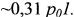

Рассмотрим ту же задачу в предположении, что оба конца стержня оперты шарнирно (рис. 3.11). Выбирая выражение для v в виде

и подставляя его в уравнение (2.6.11), придем к соотношению

(2.6.12)

(2.6.13)

Рис. 2.6.2. Комбинированное действие нагрузки на стержень, шарнирно опертый по концам

(2.6.16)

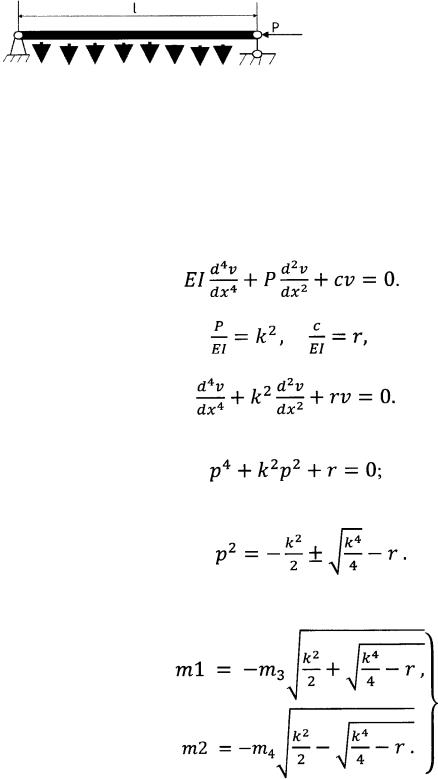
2.7. Устойчивость стержня, связанного с упругим основанием

Представим себе, что стержень, шарнирно опертый по концам, связан со сплошным упругим основанием

(рис. 2.7.1). Пусть реакция основания,

Рис. 2.7.1. Стержень на упругом основании приходящаяся на единицу длины стержня, будет пропорциональна пе­

ремещению

R=10-5cv,

размерность коэффициента с будет Па.

Дифференциальное уравнение упругой линии примем в виде (1.1.6а). При q = -Р R получим:

Если воспользоваться обозначениями

(2.7.1)

(2.7.2)

(2.7.3)

то вместо (2.7.2) будем иметь следующее однородное линейное уравнение:

(2.7.4)

Соответствующее характеристическое уравнение имеет вид

(2.7.5)

его корни будут

(2.7.6)

Примем р = ± im, где

(2.7.7)

Решение уравнения (2.7.4) получает форму

v = A sin mjx +В sin т2х +С cos т}х + D cos т2х.

(2.7.8)

Исходя из граничных условий (1.1.10), получим следующее уравнение

= 0.

Или

(2.7.9)

Приравнивая нулю sin m1l и sin m2l, получим:

п= 1, 2, 3,...

(2.7.10)

Определяя к2 по (2.7.7) и пользуясь (2.7.10), находим:

	(2.7.11)
Изогнутая линия состоит из п полуволн синусоиды
	(2.7.12)
В отличие от свободно прогибающегося стержня, здесь число полуволн
оно должно	быть определено из условия минимума нагрузки.
На рис. 2.7.2 по оси абсцисс отложены значения
отношение Р/Рэ, где Рэ	- эйлерова сила для стержня, не имеющего упругого

основания. Принимая п = 1, 2, 3,..., получим серию прямых; участки этих прямых, показанные жирной линией, являются расчетными. Переход от п-й ветви к соответствует величине г, определяемой из равенства

Рис. 2.7.2. График для расчета стержня на упругом основании

Отсюда

(2.7.13)

Соответствующие значения k будут

(2.7.14)

Если число полуволн п достаточно велико, то можно записать условие минимума k2 , приравнивая нулю производную от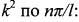

при этом

Критическая нагрузка по (2.7.14) оказывается равной

(2.7.15)

В безразмерных величинах

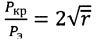(2.7.16) Формуле (2.7.16) отвечает предельная линия, показанная на рис. 2.7.2 пункти-

ром. Считая в (2.7.9)	приходим к соотношению	и, далее, к
прежней формуле (2.7.15).

З А К Л Ю Ч Е Н И Е

Задачи потери устойчивости стержневых систем, которые были рассмот­ рены, имеют на практике огромное значение. Потеря устойчивого состояния элементов конструкций зданий и сооружений, при эксплуатации которых воз­ можно возникновение различного рода динамических взаимодействий, может привести к изменению эксплуатационных характеристик конструкций или их разрушению. Яркий тому пример - потеря устойчивости элементов Волгоград­ ского моста через р. Волгу в мае 2010 г. Колебания дорожного полотна были вызваны совместным динамическим воздействием водяных волн на опоры моста и воздействием на дорожное полотно внешних периодически меняющих­ ся сил, связанных с движением транспорта. В некоторые моменты времени на часть несущих элементов конструкции моста эти силы в своей совокупности приближались к критическим значениям или даже превышали их. Именно это и вызвало периодические колебания конструкции дорожного полотна. Потеря ус­ тойчивости часто становится причиной обрушения колонн, элементов кровли, несущих стен зданий и сооружений. Продольную нагрузку, превышающую критическую, могут вызвать скопившийся снег, массивные ледяные отложения, ударные воздействия на пол в помещениях спортивных сооружений во время тренировок или соревнований, а также периодические движения людских пото­ ков в зданиях школ, вузов, предприятий и проч.

Особенно опасна динамическая нагрузка на здания и сооружения, вызван­ ная землетрясением. При большой амплитуде колебаний земной поверхности возможны частичные или полные разрушения. Существующие способы повы­ шения прочности и устойчивости зданий к землетрясениям, как показывает практика, недостаточно эффективны.

Все это подчеркивает важность поставленной задачи и необходимость пра­ вильного ее решения. В курсе сопротивления материалов рассматривались только статические методы решения задач устойчивости, которые имеют огра­ ниченное применение. В рассмотренном нами спецкурсе помимо статических методов были рассмотрены энергетические и динамические методы расчета, основанные на законе сохранения энергии. Преимущество этих методов - ши­ рота применения и возможность корректировки точности расчетных резуль­ татов. Рассматривались задачи устойчивости стержневых систем при совмест­ ном действии нескольких продольных сил, или действия продольной силы и поперечной нагрузки. Умение решать подобные задачи значительно расширяет возможности грамотного проектирования и строительства зданий и сооружений самого различного назначения. Более сложные задачи устойчивости целесооб­ разно решать с применением современных компьютерных программ.

СП И С О К Р Е К О М Е Н Д У Е М О Й Л И Т Е Р А Т У Р Ы

1.Александров А. В. Сопротивление материалов / А. В. Александров, В. Д. Потапов, Б. П. Державин. - М. : Высшая школа, 2001. - 560 с.

2.Вольмир А. С. Исследование процесса выпучивания стержней при ударе /

А.С. Вольмир, И. Г. Кильдибеков // Доклады АН СССР. - 1966. - Т. 2. - Вып. 1 0 . - С . 1 0 - 1 7 .

3.Вольмир А. С. Устойчивость деформируемых систем / А. С. Вольмир. - М. : ГИТТЛ, 1962. - 880 с.

4.Дарков А. В. Сопротивление материалов / А. В. Дарков, Г. С. Шпиро. - М. : Высшая школа, 2003. - 641 с.

5.Малышев Б. М. Устойчивость стержня при ударном сжатии / Б. М. Малы­ шев // Известия АН СССР. МТТ. - 1966. - № 4. - С. 137 - 142.

6.Пановко Я. Г. Устойчивость и колебания упругих систем / Я. Г. Пановко, И. И. Губанова. - М. : Наука, 1987. - 352 с.

7.Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев. - Киев : Наукова думка, 1989. - 732 с.

8.Тимошенко С. П. Устойчивость стержней, пластин и оболочек / С П . Тимо­ шенко. - М. : Наука, 1974. - 808 с.