Информатика / Matem

Пример 1. Если подбросить монету достаточно большое число раз, то почти наверняка можно утверждать, что примерно половину раз она упадет на «орла», а половину на «решку».

Знаменитый французский естествоиспытатель Бюффон (1707-1788)

проделал этот опыт 4040 раз, при этом выпадение «орла» равнялось 2048. Известный английский математик и биометрик Пирсон (18571936) повторил опыт 12 тысяч раз, у него число выпадений герба составило 6019. Проделав опыт 24 тыс. раз, он получил выпадение

герба в 12012 случаях. Из этих опытов видно, что доля появления герба явно стремится к ½.

Пример 2. Пример из науки о народонаселении – демографии. Наука не может предсказать пол новорожденного в каждом конкретном случае, но если рассматривать новорожденных в большом количестве, то открывается следующая закономерность: во все времена и во всех странах на каждую тысячу новорожденных приходится 514 мальчиков. Таким образом, 0, 514 – это доля мальчиков среди новорожденных. Эта закономерность была подмечена очень давно – еще в Древнем Китае за

2238 лет до нашей эры, на основании переписи населения. Правда, это число принималось равным ½.

Как видно из примеров, многие явления нам кажутся случайными только при первом взгляде на них. При более углубленном изучении обнаруживается, что на самом деле сквозь нагромождение случайностей пробивает себе дорогу закономерность. Так, в первом примере доля выпадения «решки» колеблется вокруг числа ½, во втором – доля рождения мальчиков выражается с большей точностью числом 0,514.

Закономерности такого рода и привлекли к себе внимание ученых. Для того чтобы численно выразить эту закономерность, были введены различные определения понятия вероятности. В настоящее время существует два определения: статистическое и классическое. Рассмотрим их.

2. Статистическое определение вероятности. Данное определение является наиболее часто применимым для решения практических задач.

Определение 1. Число, около которого колеблется (к которому стремится) частота появления некоторого события называется статистической вероятностью данного события.

Пример 3. В примерах о бросании монеты и рождении мальчиков (см. выше) вероятности этих событий соответственно равны: ½ и 0,514.

Классическое определение вероятности.

Прежде чем ввести определение вероятности остановимся на некоторых основных понятиях классической теории вероятности.

Пусть имеется некоторый комплекс условий S, тогда

достоверным событием называется событие, которое обязательно произойдет при выполнении комплекса условий S (пример, достоверным событием является выпадение одной из цифр от 1 до 6 при единственном бросании игрального кубика); невозможное событие – событие, которое наверняка не произойдет при выполнении комплекса условий S (пример, невозможным событием является выпадение цифры, большей 6 при одном бросании игрального кубика); случайное событие – событие, которое может произойти или не произойти при

выполнении комплекса условий S (например, случайным событием является выпадение цифры 2).

Таким образом, в теории вероятности изучаются три типа событий: достоверные, невозможные, случайные.

Комплекс выполняемых условий S называют – испытанием. А события, происходящие при этих условиях, называются исходами данного испытания.

События (исходы) принято обозначать заглавными буквами латинского алфавита (А, В, С …).

Рассмотрим основные свойства событий:

1)несовместные события – такие события, когда появление одного из них при единичном испытании исключает появление остальных (при единственном бросании кубика несовместны события А = «выпало четное число очков на игровом кубике» и В = «выпало нечетное число очков на игровом кубике»); 2)единственно возможные события – такая группа событий, когда в единичном испытании

может произойти только одно из этих событий (единственно возможными являются события: выпадение 1, выпадение 2 и т. д., при единственном бросании кубика). 3)равновозможные события – такие события, когда нет оснований предполагать, что один исход в единично испытании более возможен, чем другие (выпадение орла или решки при подбрасывании монеты, выпадение любой из цифр на игральном кубике).

Определение 2. Классической вероятностью события А называется отношение числа благоприятных исходов к общему числу несовместных единственно возможных и равновозможных исходов.

(Благоприятные исходы события – исходы, при которых данное событие произойдет обязательно).

Если классическую вероятность события А обозначить как р(А), за m обозначить число

благоприятных исходов, а за n – число общих исходов, то

(1)

Из определения 2 легко получаются основные свойства классической вероятности:

∙вероятность достоверного события равна 1;

∙вероятность невозможного события равна 0;

∙вероятность случайного события заключена между 0 и 1.

Задача 1. Найти вероятность того, что при одном бросании игрального кубика выпадет четное число.

Решение. В данном случае можем применить классическое определение вероятности, так как общие исходы являются несовместными единственно возможными и равновозможными исходами.

1)Всего на кубике шесть граней, значит n=6.

2)Граней, содержащих четные числа 3, значит m=3.

3)Если за событие В обозначить событие, при котором произошло выпадение четного числа, то по формуле (1)

4)р(В) = 3 / 6 = 1 / 2.

3. Сложение и умножение вероятностей Задача 2. Пусть событие А заключается в том, что выпадет карта бубен, а событие В – туз

пик. Какова вероятность того, что выпадет карта бубен или туз пик?

Решение. А - карта бубен, значит р(А) = ¼; В - туз пик, значит р(В) = 1 / 36; С – туз пик или карта бубен р(С) = 10 / 36. Обратим внимание, что р(С) = р(А) + р (В). Определение 3. Суммой двух событий "А" и "В" называется событие "С", состоящее в появлении события "А" или появления события "В".

Задача 3. Пусть имеем два события "А" и "В", вероятность этих событий р(А), р(В). Чему равна вероятность суммы этих событий А + В?

Решение. Имеем два случая.

1) Пусть "А" и "В" несовместны.

Событию "А" благоприятствует n(a) исходов, событию В – n (b) исходов. Тогда сумме событий А + В благоприятствует n(a) + n(b) исходов.

Пусть имеем всего n исходов. Тогда вероятность события А + В

р(А + В) = (n(a) + n(b)) / n

р(А + В) = n(a) / n + n(b) / n р(А + В) = p(А) + p(В) (2)

вероятности несовместных событий складываются.

Правило 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий.

]

2) Пусть события А и В" совместны.

Событию "А" благоприятствует n(a) исходов, событию "В" – n RU">(b)исходов. Одновременно событиям "А" и "В" соответствует n(ab) исходов. Событию А + В благоприятствуют (n(a) + n(b)) – n(ab) исходов (см. рис. 1 для совместных исходов). Тогда

р(А + В) =

р(А + В) = (n(a) / n + n(b) / n – n(ab) / n. То есть р(А + В) = р(А) + р(В) – р(АВ)

(3) Правило 2. Если события совместны, то вероятность суммы равна сумме вероятностей минус вероятность произведения этих произведений.

Задача 4. Два стрелка стреляют по цели. Вероятность попадания в цель одного стрелка 0,8, вероятность попадания второго – 0,7. Какова вероятность поражения цели, если каждый стрелок делает по выстрелу?

Решение. "А" – попадание в цель первого стрелка; "В" – попадание в цель второго стрелка. "А" и "В" – совместные события, так как попадание одного стрелка в цель не исключает возможности попадания и второго стрелка. Воспользуемся формулой сложения вероятностей двух совместных событий (2), р(А) и р(В) известны, возникает вопрос: как найти вероятность произведения двух событий?

Умножение вероятностей.

Определение 3. Два события называются независимыми, если вероятность наступления одного события не зависит от появления или не появления другого.

Определение 4. Несколько событий называются независимыми в совокупности, если каждое из них и любая комбинация остальных событий есть события независимые. Определение 5. Несколько событий называются попарно независимыми, если любые два из этих событий независимы.

Определение 6. Условной вероятностью р(В / А) называется вероятность события "В", вычисленная при условии, что условие "А" уже произошло.

Определение 7. Произведением двух событий "А" и "В" называется такое событие "С", которое состоит в совместном появлении событий "А" и "В".

Как посчитать вероятность произведения двух событий? 1. События "А" и "В" независимы.

Пусть в отношении события "А" имеются n исходов (из них n(a) благоприятных), в отношении события "В" имеется m исходов (из них m (b) благоприятных).

Сколько всего исходов в отношении А * В? n * m. А благоприятных n(а) * m(b). Тогда,

используя правило умножения ( ), найдем р(А * В):

р(А * В) =

.

р(А * В) = p(А) * p (В)(4)

Правило 3. Вероятность произведения независимых событий равна произведению их вероятностей.

В предыдущем примере события являются независимыми (почему?). Поэтому найдем их сумму р(А + В) = р(А) + р(В) – р(АВ) = 0,7 + 0,8 - 0,7 * 0,8 = 0,94.

Ответ: 0,94.

2. Пусть события "А" и "В" зависимы.

Задача 5. Брошена игральная кость. Какова вероятность того, что выпала шестерка при условии, что выпало четное число очков.

Решение. Событие "А" – четные числа (2,4,6) – три исхода благоприятствуют только шестерке. Событие "В" – шестерка. Если "А" определяет "В", то число благоприятных исходов для события "В" при условии, что событие "А" произошло равно 1, а число общих исходов 3 (так как всего три четных числа). Тогда, условная вероятность события "В" при условии, что событие "А" произошло р(В / А) = 1 / 3, р(А) = 1 / 2.

Тогда по правилу произведения р(А * В) = р(А) * р(В / А) = (1 / 2) * (1 / 3) = 1/6, где "В" – зависимое от события "А".

Ответ: 1/6.

Таким образом можно вывести общее правило.

Правило 4. Вероятность произведения двух зависимых событий равна произведению вероятности первого события на условную вероятность второго, с учетом, что первое событие уже произошло.

То есть для зависимых событий верно равенство р(А * В) = р(А) * р(В / А) Задача 6. Слепой старец вышел из пункта "А" в пункт "В" без поводыря. Какова вероятность того, что он придет в пункт "В"? (см. рис.)

Предполагается, что старец случайным образом выбирает дорогу и не идет в обратном направлении, то есть по той дороге, по которой пришел.

Вероятность попасть в каждый пункт E,C,D равна 1/3. Но далее, вероятности попасть из каждого пункта в пункт "В" разные. Из пункта "C" ведет три дороги, тогда вероятность будет 1/3, из "D" – две дороги, значит вероятность ½, из "Е" ведет одна дорога, то есть вероятность будет равна 1. Общая вероятность того, что старец попадет в пункт "В", равна:

р(В) = .

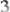
Используя правила сложения и умножения вероятностей.

Рассмотрим событие "В", которое происходит с одним и только одним из несовместных событий А1, А2, …, Аn. Известны вероятности этих событий р(А1), р(А2), …, р(Аn). Кроме, того, известны условные вероятности события "В" при условии, что события А1, А2, …, Аn произошли. Эти вероятности обозначим р(В/Аi), где i принимает значения от1 до n. Найти полную вероятность Р(В).

или

Применим формулу (2) для вероятности суммы несовместных событий:

Так как события В и Аi зависимы, то используем формулу (5) для вероятности произведения двух зависимых событий

(6)

Получили формулу полной вероятности.

Формула Байеса. Из формулы (5) вероятности произведения двух зависимых событий будем иметь:

р(В * Аi) = р(B) * р(Ai / B)= р(Ai) * p (B / i).

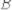
Отсюда найдем: Подставим выражение для полной вероятности (6):

(7)

где i=1,2, …, n. Получили формулу Байеса (1702-1761).

Задача 7. Истории известна легенда о том, как шах решил казнить своего звездочета. Но шах дал шанс на спасение несчастному, он сказал: «Вот тебе две пустые корзины, два черных и два белых шара. Ты можешь как угодно располагать эти шары в корзинах, но в каждой должен быть хотя бы один. Если мой палач вытянет черный шар, то тебе быть казненным. Если белый, то ты останешься жив».

Задание: как расположить шары, чтобы вероятность выжить звездочету была максимальной.

Решение: рассмотрим все варианты расположения шаров и найдем для каждого вероятность того, что будет вытащен белый шар.

1) В первой корзине 1 черный шар, а в другой 2 белых и 1 черный. Обозначим за р(А1) – вероятность того, что палач выберет первую корзину; р(А2) – вероятность того, что палач выберет вторую корзину, р(В) – вероятность того, что шар будет белым. По формуле полной вероятности: р(В) = р(А1) * р (В / А1) + р (А2) * р (В /

А2)=

2) Аналогично,

р(В) = р(А1) * р(В / А1) + р(А2) * р(В / А2) =

3) Аналогично,

р(В) = р(А1) * р(В / А1) + р (А2) * р (В / А2)= 4) Аналогично,

р(В) = р(А1) * р(В / А1) + р(А2) * р(В / А2) =

Таким образом, если звездочет поместит один белый шар в одну корзину, а второй и два черных шара в другую корзину, то вероятность, что палач вытянет белый шар, будет выше, чем при всех других раскладках шаров.

Согласно легенде, звездочет выжил.

Определение случайной величины

Определение случайной величины. Законы распределения. Числовые характеристики случайной величины. Примеры распределений.

1. Определение случайной величины Пример 1. Предположим, что в некоторой партии из 100 изделий забраковано 10 изделий.

Пусть случайным образом извлекают n изделий, среди которых могут быть и бракованные. Тогда количество бракованных изделий m среди выбранных n, величина случайная. Она может принимать значения от 0 до n, ели n<10 и от 0 до 10, если n больше 10. По законам комбинаторики можно рассчитать вероятности для каждого из значений m. Определение 1. Случайная величина – это переменная величина, которая принимает значения, зависящие от случая, и при этом можно определить вероятности этих значений. Определение 2. Дискретная случайная величина - это величина, возможные значения которой образуют дискретный набор чисел.

Дискретная случайная величина задается законом распределения вероятностей.

2. Законы распределения вероятностей. Законы распределения вероятностей как правило задаются в виде таблицы, в которой должны быть указаны значения случайной величины хi и вероятности рi соответствующих значений случайной величины. Если случайная величина принимает значения x1, х2, …, х m, то р1, р2, …, рm – вероятности, с которыми случайная величина принимает эти значения.

Сумма всех вероятностей р1 +р2 + …+ рm – это вероятность того, что в испытании будет реализовано какое-либо из значений (неважно, какое именно) х1, х2, …, хm. Эта вероятность равна единице. Таким образом данное равенство называется условием нормировки.

Например, закон распределения вероятностей при бросании кубика:

Значения		1		2		3		4		5		6
случайной

величины хi

Вероятности

рi соответствующих

значений

случайной

величины

Принято случайную величину обозначать прописной латинской буквой "Х", а значения которые принимает случайная величина – строчными латинскими буквами с индексами

Х = {х1, х2, …, хm}.

Набор вероятностей р1, р2, …, рm (или закон распределения) содержит исчерпывающую информацию о случайной величине 3. Числовые характеристики случайной величины. Часто знание закона распределения не

требуется, и тогда, используют числовые характеристики случайной величины, дающие более «грубое» представление о величине.

Основными числовыми характеристиками являются: математическое ожидание М (Х) и дисперсия D (X).

Определение 3. Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех возможных значений случайной величины на их вероятности. Таким образом:

(1)

где хi – значения дискретной случайной величины;

рi – вероятность соответствующих значений случайной величины. Определение 4. Дисперсией дискретной случайной величины "Х" называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания.

По определению:

(2)

Путем простейших математических преобразований можно получить другую формулу дисперсии, которой удобнее пользоваться для практических целей:

(2`) 4. Примеры распределений

Задача. В связке, состоящей из пяти ключей, находится один подходящий к данной скважине. Найти закон распределения случайной величины, который определяет, с какой попытки будет найден подходящий ключ.

Решение. Пусть хi – это номер "i" попытки, на которой был извлечен нужный ключ. Тогда вероятность вытащить нужный ключ с первой попытки равна

р (х1) = 1 / 5.

Вероятность вытащить нужный ключ со второй попытки равна

р

(х2)

=

где - вероятность вытащить ключ со второй попытки при условии, что при первой попытке был извлечен не нужный ключ. Тогда

р (х2) =

. Рассуждая аналогично, получим следующий закон

распределения:

Значения случайной 1 2 3 4 5 величины хi

Вероятности

рi соответствующих

значений

случайной

величины

Найдем математическое ожидание

Найдем дисперсию по формуле (2`) для этого составим таблицу для квадрата случайной величины хi2:

Значения случайной 1 4 9 16 25 величины хi2

Вероятности

рi соответствующих

значений

случайной

величины

Тогда

Ответ: М (Х) = 3; D (Х) = 2.

Генеральная совокупность. Выборка

Генеральная совокупность. Выборка. Репрезентативность выборки. Вариационный и интервальный ряд. Полигон. Гистограмма. Точечные оценки. Корреляция. Математическая статистика – раздел математики, который занимается обработкой больших массивов данных.

Имея много объектов, сложно их все проверить по какому-либо признаку. Поэтому выбирается подмножество, свойства которого отображают характерные особенности всего множества.

Определение 1. Вся совокупность объектов, подлежащих исследованию, в математике называется генеральной совокупностью, а подмножество, подвергаемое обследованию, - выборкой.

Выборка, которая адекватно отражает свойства генеральной совокупности, называется репрезентативной.

Как нужно сделать выборку, чтобы она адекватно отражала свойства генеральной совокупности?

Правило 1.Выборка будет репрезентативной, если она производится случайным образом.

Пример 1. Случайным образом подбираются люди для социологического опроса. Для репрезентативной выборки, например, выбирают случайных, встречных людей на улице. Правило 2. Если генеральная совокупность неоднородна, то нужно разделить ее на существенно различные группы и из каждой группы выбрать случайным образом одно и то же количество элементов.

Пример 2. В социологическом опросе, можно разбить людей на возрастные группы, по социальному статусу, по месту работы.

Пусть имеется выборка из n элементов, каждое из которых характеризуется значением признака хi, . Составим таблицу:

X1	X2	...	Xm
				частота
n1	n2	...	nm	появления
				признака в
				выборке
n1/n	n2/n	...	nm/n	относительная
				частота

Если частоты сложить, то получим n. n1 + n2 + … + nm = n – условие нормировки. Составим таблицу (эмпирический закон распределения):

	Xi			X1			X2		X
	p			n1 /			n2 /		nm
(xi)			n			n			/ n

Это вариационный частотный ряд, так как в нем представлены частоты появления элементов (вариантов) выборки. Частоты будут близки к вероятности, при условии, что n достаточно большое число.

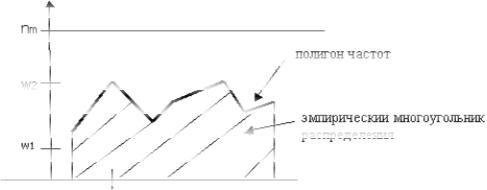
Изобразим данные таблицы на графике:

x1 x2 xm

Полученный график называется полигоном частот, а многоугольник, который ограничен графиком, осью абсцисс и прямыми х = x1 и х = x2 называется эмпирическим

многоугольником распределения.

Если сложим относительные частоты, то получим 1, ω1 + ω2 + … + ωn = 1

Если количество элементов выборки слишком велико или случайная принимает не дискретные, а непрерывные значения (например, рост человека), то в этих случаях закон распределения задается интервальным рядом.

Для того, чтобы построить интервальный закон распределения необходимо: 1)найти минимальное и максимальное значение параметра выборки; 2)затем разделить отрезок от хмин до хмакс на равные интервалы так, чтобы в каждый интервал попало хотя бы одно значение признака;

3)подсчитать количество значений признака, попавших каждый в интервал, причем, если какое-то значение признака попадает на границу интервала, то абсолютную частоту данного значения напополам относят к левому и к правому интервалу; 4)составить интервальный ряд.

Xmin n1 n2 Xmax

Таблица (интервальный закон распределения):

X		1		2		...		k
nx		n1		n2		...		nk
nx/n		n1/n		n2/n		...		nk/n

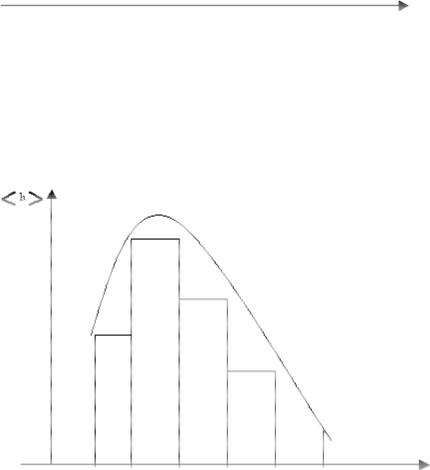
Отобразим интервальный ряд графически:

гистограмма

0 Xmin

Xmax

ω = ni / nh - высота строящегося прямоугольника.

Площадь каждого прямоугольника ni / n, сумма всех частот равна 1, значит, площадь гистограммы равна 1.

Задача. Построить интервальный ряд и гистограмму случайной величины X, где X – рост человека в случайно отобранной группе взрослых людей. Если дана выборка:

150-		160-		170-		180-		190-
160 см.		170 см.		180 см.		190 см.		200 см.
10		14		13		1		1
человек		человек		человек		человек		человек
10/39		14/39		13/39		1/39		1/39

Всего 39 человек (единиц) – число элементов выборки, 10 см – длина интервала. Построим график отражающий данную таблицу. Он называется гистограммой.

По оси абсцисс откладываются значения признака, а по оси ординат относительные частоты интервального закона распределения частот.