814. 2. непрерывность сплайна g_i-1(x_i-1)=g_i(x_i-1), i= 2, 3, …,n; (уравнений (n-1))

815. 3. непрерывность производной g^_i-1(x_i-1)=g^_i(x_i-1), i= 2, …,n; (уравнений (n-1))

816. 4. непрерывность второй производной g^_i-1(x_i-1)=g^_i(x_i-1), i= 2,…,n; (n-1)

817. 5. краевые условия g^₁(x₀)=0, g^_n(x_n)=0. (два уравнения)

818. Для i-ой составляющей сплайна имеем:

819. g_i(x)=a_i+b_i(x-x_i)+c_i(x-x_i)²+d _i(x-x_i)³,

820. g^_i(x)=b_i+2c_i(x-x_i)+3d₁(x-x_i)²,

821. g^_i(x)=2c_i+6d_i(x-x_i).

822. Полагая для краткости узлы равноотстоящими: h=x_i-x_i-1, i=1,2,…, n, получим детализированную систему уравнений:

823. a₁-b₁h+c₁h²-d₁h³=f₀ , a_i=f_i, i=1,2,…, n;

824. a_i-1= a_i-b_ih+c_ih²-d₁h³, i= 2, 3, …,n;

825. b_i-1=b_i-2c_ih+3d_ih², i= 2, 3, …,n;

826. c_i-1=c_i-3d_ih, i= 2, 3, …,n;

827. c₁-3d₁h=0, с_n=0.

828. Всего получается 4n уравнений т.е. столько же сколько и неизвестных.

830. Теорема о степени приближения кубическим сплайном:

831. Если функция f(x) принадлежит классу четырежды дифференцируемых на отрезке [а,b] функций: f(x)C⁴[a,b], то кубический сплайн g(x) удовлетворяет неравенствам:

832. maxf^(m)(x)-g^(m)(x) Kh^4-m maxf⁽⁴⁾(x) при axb и m=0, 1, 2;

833. т.е. f(x)-g(x)= O(h⁴), f (x)-g(x)= O(h³), f (x)-g(x)= O(h²).

834. Замечание: Благодаря большей простоте записи естественные сплайны получили значительное распространение. Однако искусственное наложение условий f ^(a)=0 и f ^(b)=0 при интерполяции функций, которые этим условиям не удовлетворяют, приводит к значительной потере точности. Вместо четвертого порядка естественный сплайн обладает лишь вторым порядком точности. Если использование естественного сплайна не вызвано какими-либо специальными причинами, то следует, по-видимому, отказаться от него в пользу кубического сплайна с граничными условиями другого типа.

839. 45.Метод наименьших квадратов .

840. При обработке результатов измерений часто возникает необходимость построить эмпирическую формулу, дающую аналитическое выражение функциональной зависимости, заданной таблицей. Использование для этого интерполяционных полиномов не всегда целесообразно, так как зачастую результаты измерений помимо основной зависимости отражают разного рода малые случайные ошибки, и точное совпадение в узлах интерполяции построенной функции с табличными значениями может даже исказить основную зависимость. В других случаях речь может идти о построении наиболее простой формулы, достаточно хорошо отражающей указанную зависимость. Пусть результаты измерений представлены совокупностью измеренных значений функции в соответствующих точках f(x_i), i=0,1,…,n. Требуется найти функцию (x) в виде некоторой эмпирической формулы, которая аппроксимирует функцию f(x), так чтобы отклонения v_i=(x_i) - f(x_i), i=0,1,…, n оказались бы в каком-то смысле наименьшими. Наиболее распространенным критерием малости отклонений является следующий критерий, положенный в основу способа наименьших квадратов. Требуют, чтобы оказалась минимальной сумма квадратов отклонений 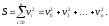Будем искать аппроксимирующую функцию в виде полинома степени m: (x) = b₀+b₁x+…+b_mx^m (b_m0). Задача ставится следующим образом: подобрать коэффициенты полинома: b₀, b₁,…, b_m, так чтобы сумма квадратов отклонений S достигала минимума. Заметим, что величина S является неотрицательной функцией переменных b₀, b₁,…, b_m и, следовательно, всегда имеет минимум. Если m>n, то существует бесконечное множество полиномов степени m, обеспечивающих S=0. Для m=n равенство S=0 обеспечивается единственным полиномом, являющимся интерполяционным полиномом для заданной функции. Обычное соотношение между степенью полинома и числом узлов: m<<n, в этом случае при любых значениях коэффициентов полинома S>0. Таким образом, задача сводится к исследованию на минимум функции многих переменных S(b₀, b₁,…, b_m). Необходимым условием минимальности S является равенство нулю производных по всем параметрам: S/b₀=0, S/b₁=0, …, S/b_m=0.

841. S/b₀=2ⁿ_i=0(b₀+b₁x_i+…+b_mx_i^m –f(x_i)),

842. S/b₁=2ⁿ_i=0(b₀+b₁x_i+…+b_mx_i^m- f(x_i))x_i,

843. … … …

844. S/b_m=2ⁿ_i=0(b₀+b₁x _i …+b_mx_i^m-f(x_i))x_i^m.

845. Преобразование уравнений дает систему, назывемую системой нормальных уравнений:

846. (n+1)b₀+b₁ⁿ_i=0x_i+ b₂ⁿ_i=0x_i²+…+b_mⁿ_i=0x_i^m = ⁿ_i=0f(x_i)

847. b₀ⁿ_i=0x_i +b₁ⁿ_i=0(x_i)²+…+b_mⁿ_i=0(x_i)^m+1 = ⁿ_i=0x_if(x_i)

848. … … …

849. b₀ⁿ_i=0x_i^m+b₁ⁿ_i=0x_i^m+¹+…+b_mⁿ_i=0x_i²^m = ⁿ_i=0x_i^mf(x_i)

850. Решая эту систему уравнений с симметричной матрицей, найдем коэффициенты полинома: b₀,b₁,…,b_m. Если среди узлов нет совпадающих, то определитель системы отличен от нуля, и так как значения функции не могут быть все одновременно нулями, то система имеет единственное решение. Если известна погрешность измерения единичного значения функции - , то величина максимального отклонения =maxv_i (i=0,1,…, n) может служить обоснованием правильности выбора степени аппроксимирующего полинома m. Если максимальное отклонение полинома от функции много больше погрешности измерения: >>, то это означает слишком грубую аппроксимацию, и степень m необходимо увеличить. В противном случае - <<, степень m завышена и ее следует уменьшить. Только когда , можно считать, что степень аппроксимирующего полинома выбрана правильно.