
12.3. О траектории движения частицы.
Найдем уравнение траектории частицы, движущейся в поле центральных сил.
Представим компоненты импульса, записанного в полярных координатах, следующим образом:
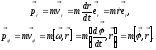 (12.14)
(12.14)
Далее,
т.к. угол между вектором угловой скорости
 и
радиус-вектором
и
радиус-вектором
 равен
равен
 ,
то
,
то
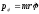 .
.
Тогда из (12.10а, 12.12 и 12.14) для энергии и момента импульса частицы, движущейся в центральном поле, получаем
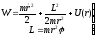 .
(12.15)
.
(12.15)
Из первого уравнения (12.15) получаем
 .
.
Разделяя
переменные, находим в неявном виде
зависимость
 :
:
 .
(12.16)
.
(12.16)
Из второго уравнения (12.15) имеем
 .
.
Исключив
из уравнений (12.15) время
 ,
находим уравнение траектории частицы
в центральном поле в полярных координатах
(связь между
,
находим уравнение траектории частицы
в центральном поле в полярных координатах
(связь между
 и
и
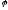 ):
):
 .
(12.17)
.
(12.17)
Интегралы
(12.16) и (12.17), вообще говоря, могут быть
вычислены, если известен явный вид
функции
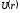 .
.
12.4. Границы движения.
Из
первого уравнения (12.15) следует, что
значения
 ,
при которых энергия частицы равна
,
при которых энергия частицы равна
 ,
(12.18)
,
(12.18)
определяют
границы области движения по расстоянию
от центра поля, поскольку при выполнении
равенства (12.18) радиальная скорость
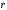 обращается в нуль. Однако равенство
нулю (
обращается в нуль. Однако равенство
нулю (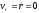 )
радиальной составляющей скорости не
означает,
что частица остановилась, т.к. азимутальная
(угловая) компонента скорости отлична
от нуля (
)
радиальной составляющей скорости не
означает,
что частица остановилась, т.к. азимутальная
(угловая) компонента скорости отлична
от нуля ( ).
Это утверждение вытекает из требования
).
Это утверждение вытекает из требования
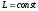 для поля центральных сил.
для поля центральных сил.
Равенство
 определяет “точку поворота” траектории,
в которой функция
определяет “точку поворота” траектории,
в которой функция
 достигает либо максимального, либо
минимального значения, после чего
начинает соответственно убывать или
возрастать.
достигает либо максимального, либо
минимального значения, после чего
начинает соответственно убывать или
возрастать.
Если
область допустимого изменения
 ограничена лишь условием
ограничена лишь условием
 ,
то движение частицы инфинитно
– её траектория приходит из бесконечности
и уходит на бесконечность.
,
то движение частицы инфинитно
– её траектория приходит из бесконечности
и уходит на бесконечность.
Если
область изменения
 имеет две границы
имеет две границы
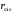 и
и
 ,
то движение является финитным и траектория
частицы лежит внутри кольца, ограниченного
окружностями
,
то движение является финитным и траектория
частицы лежит внутри кольца, ограниченного
окружностями
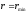 и
и
 ,
определяющими границы движения. Однако
траектория при этом может оставаться
незамкнутой.
,
определяющими границы движения. Однако
траектория при этом может оставаться
незамкнутой.
За
время прохождения одной петли (от
 до
до
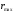 и снова до
и снова до
 )
радиус-вектор частицы совершит поворот
на угол
)
радиус-вектор частицы совершит поворот
на угол
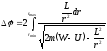 .
(12.19)
.
(12.19)
Условие
замкнутости траектории:
траектория будет замкнутой, если
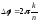 ,
где
,
где
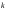 и
и
 - целые
- целые
числа,
т.е. за одну петлю радиус-вектор должен
повернуться 
на
угол, равный рациональной части от
 .
.
Тогда
через
 повторений этого периода времени радиус-
повторений этого периода времени радиус-
вектор
точки, сделав
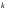 полных оборотов, совпадет со своим
полных оборотов, совпадет со своим
первоначальным значением, т.е. траектория замкнется.
Однако такой исход является скорее исключением,
нежели правилом. Существуют лишь два типа центральных
полей, в которых все траектории финитных движений
замкнуты. Это поля, где зависимость потенциальной энергии
от расстояния от центра поля имеет вид:
 .
.
