книжка умняшкина по моцос

квантование ˆ				ˆ				2	2	/12 . Эта
Y →Y для любого преобразования				Y − Y					~ Nu

ошибка всегда равна ошибке, внесенной в исходный вектор X, только для ортогональных преобразований (см. пример 3.8). Если анализируемые преобразования не являются ортогональными, то говорить об экви-

валентности ошибки кодирования

ˆ

2

~ Nu

2

/12

для разных пре-

X − X

образований нельзя и сравнение декоррелирующей эффективности преобразований по параметру (5), основанному на понятии дифференциальной энтропии, является некорректным.

Замечание. Из формулы (5) следует, что самый «худший» вариант используемого преобразования, при фиксированной размерности N, дает максимальное значение параметра

N −1
P = ∏σk2 .	(6)

k =0

N −1

Наложив ограничение ∑σk2 = const (см. лемму 1), методом неопреде-

k =0

ленных множителей Лагранжа можно было бы убедиться в том, что

максимум выражения (6) имеет место, когда σ 2 = σ 2 = K= σ 2 −

0 1 N 1

(удобнее искать максимум от логарифма выражения (6)). То есть наихудший случай имеет место тогда, когда суммарная дисперсия (фактически, энергия) равномерно распределена по всем коэффициентамтрансформантам. Оптимальность же применения преобразования можно понимать как способность последнего к концентрации основной энергии исходного дискретного сигнала (вектора X) в малом количестве коэффициентов-трансформант – в этом смысле задача подбора преобразования принимает вид задачи дискретной L2-аппроксимации: найти такое преобразование, чтобы для заданного набора Ω отбрасываемых

коэффициентов их суммарная дисперсия (энергия) ∑σk2 была мини-

k Ω

мальной. Использование такого подхода к анализу эффективности применения преобразований для кодирования данных менее универсально, оно вполне может дать разные результаты сравнения преобразований при различном количестве отбрасываемых коэффициентов. Тем не менее, подобное изучение свойств преобразований обосновано и описано в литературе.

131

N − N2 = yN / 2

= aN / 2

6.4. ДПФ в вещественной форме

При выводе критерия средней избыточной энтропии (5) предполагалось, что ортогональное преобразование, определяемое матрицей W – вещественное. Вместе с тем, при использовании ДПФ (3.12), имеющего комплексную природу, для обработки вектора X из N вещественных компонент в векторе-спектре Y получаем уже N, вообще говоря, комплексных коэффициентов (2N вещественных чисел). Двойную избыточность преобразованных данных можно устранить, если воспользоваться свойством 1° ДПФ (см. раздел 3.5). Для коэффициента ДПФ (3.12) yk обозначим: ak=Reyk, bk=Imyk. Тогда при обработке вещественного вектора X получим y0=a0 и, если размерность преобразования N есть четное число: yN / 2 = y ; остальные спектральные коэффици-

енты в общем случае являются комплексными числами и в силу свойства 1° ДПФ:

yk = 1

N

−1

2πi

kj =

1

N −1

2πi kj +i −1

N −1

2πi kj = ak

∑x j e−

N

∑x j cos

∑x j sin

+ibk ,

N j=0

N

j=0

N

N

j=0

N

144424443

144424443

ak

bk

N −1

2πi

N −1

N −1

yN −k =

1

∑x j e

N

kj =

1

∑x j cos2πi kj +i

1

∑xj sin 2πi kj =ak −ibk .

N

j=0

N

j=0

N

N

j=0

N

144424443

144424443

aN−k

bN−k

Из вектора-спектра Y, полученного в результате ДПФ вещественного

(

вектора X, сформируем вектор Y по следующему правилу:

N −1

ak

= yk

=

1

∑x j cos 2πi kj,

для k = 0 или

k = N / 2

N

j =0

N

(

2

N −1

2πi

2 =

∑x j cos

kj, для 1 ≤ k < N / 2

,

(7)

yk

= ak

N

N

j =0

2

N −1

2πi kj,

−bk 2

=

∑x j sin

для N / 2 < k ≤

N −1

N

j =0

N

k = 0,1,K, N −1 .

Лемма 2. Дискретное преобразование вещественного вектора X в век-

(

(

, определяемое формулой (7), является ортогональным.

тор Y = WX

132

◄ Пусть число N – четное число. Так как bk=-bN-k, ak=aN-k то

	N −1			N −1			N	−1
							2
	∑bk2 =			∑bN2 −k =			∑ bk2 ,
	k =	N	+1	k =	N	+1	k =1
	2			2

(

Для евклидовой нормы вектора Y

	N −1			N −1			N	−1
							2
	∑ak2 =			∑aN2 −k =			∑ ak2 .
	k =	N	+1	k =	N	+1	k =1
	2			2
	имеем:

N −1

N

−1

N −1

(

2

y0

2 +

yN / 2

2

Y

=

∑y(k2 =

2

+ ∑ 2ak2 +

∑2bk2 =

E

k =0

k =1

k =

N

+1

2

N

=

y0

2 +

2∑−1 (ak2 + bk2 )+

yN / 2

2 +

N∑−1(ak2 + bk2 )= N∑−1

yk

2 =

Y

2E .

k =1

k =

N

+1

k =0

2

В силу унитарности ДПФ (см. раздел 3.5) для любого вектора X имеем

(

Y E = X E , поэтому Y E = X E . Поскольку (см. также лемму 3.1)

XT X = X 2E = Y( 2E = Y(T Y( = XT W( T W( X , то W( T = W( −1 . ►

Преобразование (7) назовем ДПФ в вещественной форме, или вещественным ДПФ (ВДПФ).

6.5. Дискретный марковский процесс первого порядка. Дискретное косинусное преобразование

Одной из важнейших корреляционных моделей для дискретных сигналов является модель дискретного марковского процесса первого порядка. Данный процесс является стационарным, т.е. его параметры не зависят от момента наблюдения. Стационарность (в широком смысле) дискретного процесса означает, что отсчёты дискретного сигнала {Xk} имеют одинаковые математические ожидания M(Xk)=mX и дисперсии

D(Xk)= σX2 , а корреляция между отсчетами Xk, Xj зависит только от рас-

стояния между моментами наблюдения дискретного процесса, т.е. от величины |k-j|. Так, для марковского процесса первого порядка коэффи-

циент корреляции r( X k , X j ) = ρ k − j , где ρ - коэффициент корреляции соседних отсчётов сигнала. Тогда случайный вектор X = (X 0 ,K, X N −1 )T

133

- выборка из дискретного сигнала, описываемого моделью марковского процесса, имеет следующую ковариационную матрицу:

				1		ρ	K ρN −1
	(ρ)=σ2			ρ		1	KρN −2
K								.	(8)
X	X		L			L	L L
			ρ	N −1	ρ	N −2	K 1

Не меняя общности рассуждений, можно считать далее дисперсию процесса единичной, D(Xk)= σX2 =1. Модель (8) представляет особый инте-

рес, так как часто используется на практике для описания дискретных сигналов, причём обычно параметр ρ имеет значение, близкое к единице.

Среди преобразований, имеющих быстрые алгоритмы вычислений (требующих ~NlogN операций умножения вместо ~N2), наибольшую эффективность для кодирования сигнала, описываемого моделью мар-

ковского процесса, показывает дискретное косинусное преобразование

(ДКП), которое определяется следующей формулой:

		2		N −1	πk		1
	yk =		c(k )∑x j		cos	(j +		) ,	(9)
		N					2
				j =0	N
			k = 0,1,K, N −1,
где		1	2 ,	при	k = 0 .
	c(k )=
			1,	при	k ≠ 0

Записав ДКП (9) в матричном виде, Y=WX, получим для структуры

матрицы ДКП:	W =		w	=	2	πk		N −1		. Выясним
						N c(k) cos	(j + 1 )
			k, j			N	2
								k , j =0

«происхождение» формулы (9), для чего покажем, как связано ДКП с непрерывным преобразованием Фурье по тригонометрической системе.

Если для некоторого сигнала f(t), заданного на отрезке наблюдения t [0,T], составить ряд Фурье (2.3) с коэффициентами, найденными по

		f (t)	f((t)
			t
-T	0	T	2T

134

формуле (2.4), то свойства сходимости полученного ряда Фурье будут определяться характером функции f (t) , которая представляет собой

периодическое продолжение с периодом T на всю числовую ось функции f(t).

С точностью до нормировочного множителя ДПФ представляет собой приближенное вычисление первых коэффициентов ряда Фурье по формуле прямоугольников:

1 T

2πk

1 N−1

2πk

1

N−1

−i

2πkj

c

k

=

∫

f (t)exp

−i

t dt ≈

∑

f ( j∆t)exp

−i

j∆t ∆t =

∑

x

j

e

N ,

T

T

T

T

N

0

j=0

j=0

где N=T/∆t, xj=f(j∆t). Наличие данной связи позволяет предположить: чем выше скорость сходимости ряда (2.3), тем более выражена локализация энергии в векторе трансформант ДПФ.

Для лучшей сходимости ряда (2.3) (т.е. для более быстрого убывания абсолютных величин коэффициентов Фурье) желательно, чтобы

функция f (t) была непрерывной. Для того чтобы этого добиться, сна-

чала дополним функцию f(t) четным образом на отрезке t [-T,0], а затем полученную функцию (заданную уже на области t [-T,T] ) продолжим на всю числовую ось с периодом 2T, см. рис.

		f (t)	f (t)
			t
-T	0	T	2T

Для полученной функции f (t) периода 2T Фурье (2.3). В силу четности функции f (t)

1

T (

−i

2πk

t

1

T (

πk

ck =

∫

f (t) e

2T dt =

∫

f (t) cos

t

2T

2T

T

−T

−T

найдем коэффициенты ряда имеем:

	i	T	(	πk
dt −		∫	f (t) sin		t dt	=
	2T	−T		T
		144424443

							0
		1	T	πk
	=		∫ f (t) cos			t dt .	(10)
		T			T
			0
							135

Получаем, что коэффициенты Фурье вещественные и ck=c-k. Подсчитаем приближенно значение интеграла (10) по квадратурной формуле прямоугольников, выбрав на этот раз узлы в точках x j = f (( j + 0.5)∆t) (вновь

N=T/∆t):

1 T

πk

1

N −1

πk

c

k

=

∫

f (t) cos

t dt ≈

∑

x

j

cos

( j + 0.5) .

T

T

N

N

0

j =0

Полученное выражение с точностью до нормировочного множителя совпадает с формулой ДКП (9). Оказывается, выбор узлов квадратурной формулы прямоугольников в точках x j = f (( j + 0.5)∆t) обеспечивает

ортогональность ДКП.

Лемма 3. Матрица W ДКП (9) ортогональна.

◄ Необходимо показать, что матрица U = WWT является единичной. В соответствии с определением (9) получаем для произвольного элемента матрицы U:

N −1

2

N −1

πk

1

πm

1

uk,m = ∑wk, j wm, j

=

c(k)c(m) ∑cos

(j +

) cos

(j +

)

=

N

N

2

N

2

j =0

j =0

1

π(k + m)

N −1

π(k − m)

N −1

1

1

=

c(k)c(m)

∑cos

(j +

)

+ ∑cos

(j +

)

,

N

N

2

N

2

j =0

j =0

14444244443

14444244443

s(k +m)

s(k −m)

k=0,…,N-1; m=0,…,N-1.

N −1

π l

1

Найдем значение суммы

s(l) = ∑cos

(j +

)

= s(−l)

для значений

2

j =0

N

l=0,…,2N-2. Очевидно, s(0)=N, а при значениях l=1,…,2N-2 получаем по формуле для суммы геометрической прогрессии:

N −1

π l (j+

1

)

π l

iπl

iπl

i

i

1 − e

1 − e

2N

∑e

N

2

s(l) = Re

= Re e

= Re

=

πl

πl

πl

j=0

1 − e

i

N

−i

i

e

2N − e

2N

iπl

πl

i

πl

−i

πl

sin

πl

e

−1

2

= Re

i

2

e

2 − e

2

= Re

i

l

= 0

,

πl

= Re e

πl

πl

2i sin

2i sin

sin

2N

2N

2N

136

поскольку стоящее в скобках выражение является мнимым при нечет-

ных значениях l, а при четных значениях l получаем sin

πl =0. Тогда

2

= c(k)c(m) (s(k + m) + s(k − m))=

0,

приk ≠ m

u

k,m

2c(k)c(m), приk = m = 0

,

N

c(k)c(m), приk = m ≠ 0

0, приk ≠ m

1

,

при

j = 0

откуда uk,m

,

поскольку

2

. ►

=

= m

c(j)=

1, приk

1,

при

j ≠ 0

Следствие. Доказанная лемма означает, что обратное ДКП определяется

следующей формулой:

x j =

2

N −1

πk

N

∑c(k ) yk cos

(j + 12 ) ,

(11)

k =0

N

j = 0,1,K, N −1.

ДПХ

ДПА

ВДПФ

ДКП

0.35

∆Н, бит

0.07

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

ρ

Рисунок 6.2. Значения средней избыточной энтропии (5) при использовании

некоторых ортогональных преобразований для обработки 16-ти компонентного

вектора данных, описываемого ковариационной матрицей (8)

137

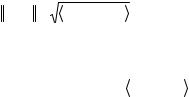
Для иллюстрации декоррелирующих свойств ДКП приведем расчетные значения средней избыточной энтропии (5) при использовании некоторых дискретных преобразований для обработки вектора X, который состоит из 16 компонент и представляет собой реализацию стационарного марковского процесса первого порядка с ковариационной матрицей (8). На графике рисунка 6.2 приведены результаты, включающие ДПФ в вещественной форме, ДКП, дискретные преобразования Уолша (ДПУ) и Хаара (ДПХ) (определения двух последних преобразований см. в главе 1). Наиболее близкие характеристики к оптимальному преобразованию Карунена-Лоэва, как видим, дает ДКП, причём явное преимущество ДКП наблюдается для различных значений параметра ρ.

ДКП нашло практическое применение во многих, в том числе стандартизованных, алгоритмах сжатия дискретных сигналов.

6.6. Аппроксимационный подход к выбору преобразований для кодирования дискретных сигналов. Частотная трактовка

Ранее мы отмечали, что целью использования преобразований является перевод коррелированного набора данных X в менее коррелированный (в идеале – независимый) набор данных – вектор Y. Именно с такой точки зрения мы и рассматривали вопрос эффективности применения преобразований в схемах компрессии дискретных сигналов, отметив попутно (см. замечание к разделу 6.3) важность неравномерного распределения энергии по компонентам преобразованного вектора Y, когда основная часть энергии дискретного сигнала должна быть сконцентрирована в малом количестве компонент-трансформант. На этом принципе будем основывать дальнейшие рассуждения.

Рассматривавшиеся нами дискретные ортогональные преобразования (Фурье, Уолша, Хаара, ДКП) были получены в результате дискретизации непрерывных преобразований по некоторой ортогональной сис-

теме функций {ϕk (t)}∞k =0 (для упрощения изложения будем считать, что система ортонормирована, ϕk (t) = ϕk (t),ϕk (t) =1), когда исходный

∞

аналоговый сигнал представляется в виде x(t) = ∑ckϕk (t) , а дискрет-

k =0

ный - x j = x( j∆t) = N∑−1 ykϕk ( j∆t) , где yk ≈ ck = x(t),ϕk (t) . При этом

k =0

138

для энергии сигналов в непрерывном и в дискретном случае, в силу ортогональности преобразований (см. теорему 1.10 и лемму 3.1) имеем:

∞	N −1				2	N −1				2 . Мы уже отмечали, что кон-
< x(t), x(t) >= ∑ck2	и ∑		xk			= ∑		yk
k =0	k =0					k =0

центрация основной энергии в малом количестве коэффициентов обобщенного спектра – это цель, которую необходимо достигнуть при использовании преобразования. Для ее достижения необходимо построить

такой полный ортогональный базис {ϕk (t)}∞k =0 , который позволяет дос-

∞

таточно точно представить непрерывный сигнал x(t) = ∑ckϕk (t) ма-

k =0

n

лым количеством слагаемых ряда: x(t) ≈ xn (t) = ∑ckϕk (t) . При этом

k =0

квадрат ошибки, связанной с отбрасыванием коэффициентов ряда, ра-

∞

вен x(t) − xn (t) 2 = ∑ck2 . Поставим следующую задачу: найти такой

k =n +1

базис {ϕk (t)}∞k =0 , который давал бы минимальную ошибку x(t) − xn (t) (в выбранной норме) для заданного класса сигналов x(t) и фиксированного числа n. Мы будем рассматривать норму f (t) = < f (t), f (t) > .

Сформулируем требования к базису {ϕk (t)}∞k =0 с точки зрения частот-

ных спектральных характеристик.

Частотный подход к исследованию реальных сигналов основан на том, что для сигналов f(t), представимых в виде интеграла Фурье (2.5):

+∞

f (t) = ∫S(ν) e2πiνt dν , необходимым условием существования данного

−∞

несобственного интеграла является равенство lim S(ν) e2πiνt = 0 , т.е.

ν →∞

«затухание» спектральной плотности с увеличением частоты1:

1 При рассмотрении сигналов на конечных временных интервалах при разложении в тригонометрический ряд (2.1) или (2.3) соответствующее свойство коэф-

фициентов Фурье {ck} принимает вид: lim ck = 0 (лемма Римана-Лебега).

k →∞

139

lim S(ν) = 0 . Поэтому на практике частотный спектр сигнала можно с

ν →∞

той или иной точностью считать ограниченным (см. также раздел 2.3) некоторой полосой ν [-F;F]. Физическая трактовка данного явления связана с тем, что любая электротехническая система обладает инертностью, которая ограничивает скорость изменения сигнала f(t), описывающего какой-либо процесс в системе (например, скорость изменения напряжения или тока ограничена наличием паразитных емкостей и индуктивностей электрической цепи). Поэтому основная энергия сигнала в характеризующей его частотной полосе ν [-F;F], как правило, локализована в области низких частот, так как высокочастотные составляющие спектра вносят ощутимый вклад лишь в быстро изменяющихся во времени сигналах.

Из приведенных соображений следует, что, выполнив ДПФ дискретного сигнала, обычно можно без особого ущерба для точности последующего восстановления сигнала обнулить высокочастотные коэффициенты дискретного спектра (3.12), приходящиеся на те частотные

отсчеты из множества {yk }kN=−01 , номера которых близки к N/2 (см. также пример 8 главы 3).

Помимо тригонометрической системы, для представления сигналов

∞

в виде ряда x(t) = ∑ckϕk (t) можно использовать и другие функцио-

		k =0
нальные базисы	{ϕ	k	(t)}∞	, для которых lim c	k	= 0	(необходимое усло-
			k =0	k →∞

вие сходимости функционального ряда). Основной вопрос при этом заключается в следующем: какую функциональную базисную систему использовать предпочтительнее? Приведенные выше рассуждения о природе спектров реальных сигналов позволяют предположить, что

частотные спектры используемых базисных функций {ϕk (t)}∞k =0 должны

различаться, образуя выраженные низко- и высокочастотные наполнения - тогда заранее можно будет предположить, что коэффициенты Фурье, соответствующие высокочастотным базисным функциям, будут

∞

вносить малый вклад в разложение x(t) = ∑ckϕk (t) . Рассматривавшие-

k =0

ся нами в главе 1 системы Уолша, Хаара обладают такими общими свойствами: с увеличением номера базисной функции ее локализация в частотной области смещается в сторону высоких частот.

140