Математическое ожидание (среднее, среднее значение)

Математическое ожидание – это среднее значение случайной величины (теоретическое среднее). М.о. – одна из важнейших вероятностных характеристик случайной величины.

Буквенное обозначение математического ожидания случайной величины X : M(X).

Для дискретной случайной величины X математическое ожидание вычисляется как полная сумма произведений значений случайной величины на вероятности этих значений:

M(X) = x₁  P(x₁) + x₂  P(x₂) + … + x_N  P(x_N) =,

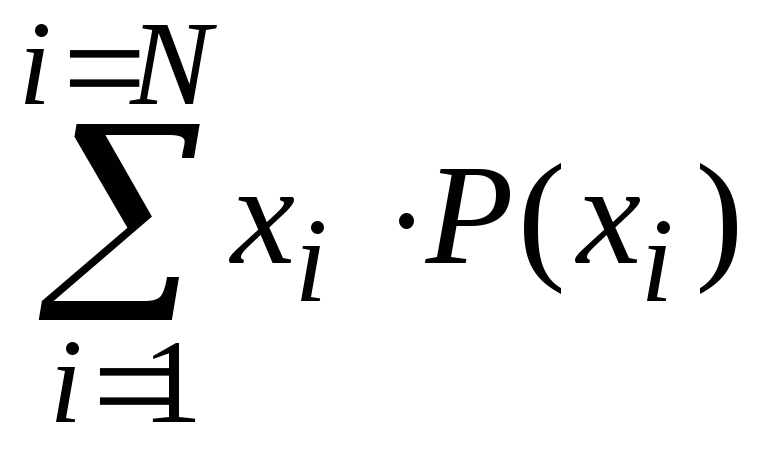где N – число возможных значений случайной величины X.

Для непрерывной случайной величины X математическое ожидание вычисляется как

M(X) =

Математическое ожидание для дискретной случайной величины численно равно абсциссе центра закона распределения, для непрерывной случайной величины – абсциссе центра плотности распределения.

Термином математическое ожидание M(X) обозначается не только вероятностная характеристика, но и так называемая операция усреднения, т.е. взвешенное суммирование с весами, равными значениям закона распределения P(x_i), или интегрирование с ядром, равным плотности распределения p(x).

Запись M(…) используется для обозначения не только математического ожидания случайной величины X, но и для так называемой операции усреднения, т.е. суммирования с множителями (весами), равными значениям закона распределения P(x_i), или интегрирования с ядром, равным плотности распределения p(x).

Математическое ожидание совпадает с абсциссой центра тяжести закона распределения или плотности распределения. В ряде случаев близко к наиболее вероятному значению.

Дисперсия (рассеяние)

Дисперсия – это вероятностная характеристика степени рассеяния возможных значений случайной величины относительно её математического ожидания.

Буквенное обозначение дисперсии случайной величины X : D(X).

Дисперсия численно равна среднему квадрату отклонения случайной величины от своего среднего (математического ожидания):

D(X) = M( ( X – M(X) )² ).

Для дискретной случайной величины дисперсия вычисляется так:

D(X) = (x₁–M(X))² P(x₁) + … + (x_N–M(X))² P(x_N) =.

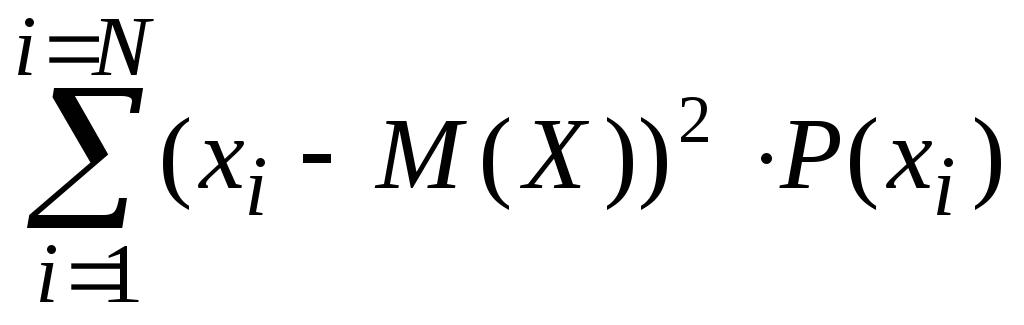Для непрерывной случайной величины

D(X) = .

Единица измерения дисперсии – квадрат единицы измерения случайной величины.

Среднеквадратическое отклонение (стандартное отклонение)

Среднеквадратическое отклонение также как и дисперсия характеризует отклонение возможных значений случайной величины от математического ожидания, являясь вероятностной характеристикой закона распределения или плотности распределения.

Среднеквадратическое отклонение вычисляется как квадратный корень из дисперсии

.

В отличие от дисперсии, среднеквадратическое отклонение удобно тем, что измеряется в тех же единицах измерения, что и сама случайная величина.

Нормальное распределение (распределение Гаусса)

Нормальное распределение – особый вид плотности распределения непрерывной случайной величины

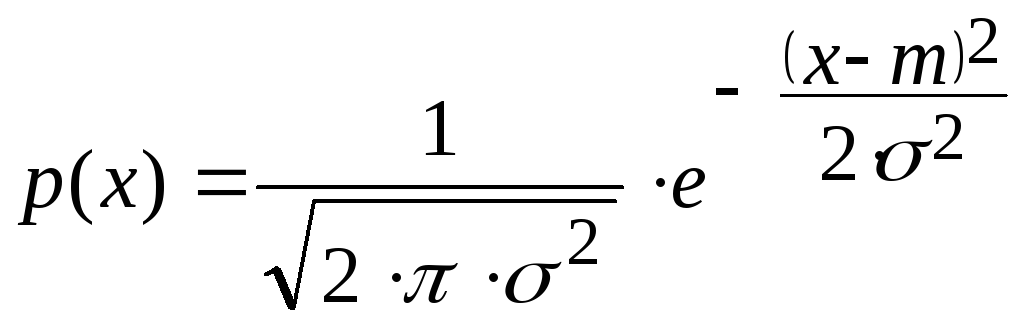= N ( m;  ²) .

Нормальное распределение N ( m;  ²) зависит только от двух параметров, название которых соответствует их смыслу: m – математическое ожидание;  ² – дисперсия.

График нормального распределения представляет собой гладкую симметричную «колоколообразную» кривую с быстро убывающими «хвостами». Максимум нормального распределения располагается над точкой математического ожидания. Ширина вершинной части кривой определяется дисперсией. Чем дисперсия больше, тем кривая шире. И, при этом, ниже – для сохранения единичности площади под кривой.

Нормальное распределение возникает везде, где суммируется множество близких по силе случайных воздействий, причём вероятностные характеристики каждого из них не существенны. Поэтому нормально распределённые случайные величины имеют весьма широкое распространение.