
- •17. Понятие фундаментальной системы решений линейных однородных диф уравнений.Вронскийан.
- •50.Ряды Тейлора и Маклорена. Вывод формулы для общего члена ряда Маклорена.
- •20. Лоду с пос коэф. Второго порядка
- •54. Вывод формулы Эйлера с помощью рядов Маклорена
- •24. Определение изображения по заданному оригиналу.
- •55.Биноминальный ряд
- •25. Определение изображения по заданному оригиналу.
- •56. Применение рядов для вычисления пределов
- •29. Преобразование Лапласа. Свойство подобия.
- •30 Преобразование лапласа. Интегрирование оригинала.
- •31 Преобразование Лапласа. Теорема запоздания.
50.Ряды Тейлора и Маклорена. Вывод формулы для общего члена ряда Маклорена.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
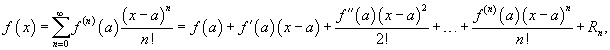
где Rn − остаточный член в форме Лагранжа определяется выражением

Если
приведенное разложение сходится в
некотором интервале x,
т.е. ![]() ,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
![]()
Разложение некоторых функций в ряд Маклорена

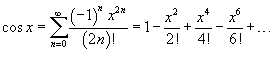
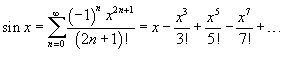

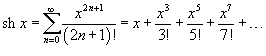
Доказательство
Операторные соображения[
Перед
доказательством удобно рассмотреть
соображения высшего порядка (принадлежащие
Лагранжу) о том, почему такая формула
имеет место. Обозначим ![]() —
разностный оператор,
—
разностный оператор, ![]() —
оператор суммирования,
—
оператор суммирования, ![]() —
оператор дифференцирования,
—
оператор дифференцирования, ![]() —
оператор интегрирования.
—
оператор интегрирования. ![]() обратен
к
обратен
к ![]() ,
а
,
а ![]() -
обратен к
-
обратен к ![]() .
Можно выразить
.
Можно выразить ![]() через
через ![]() с
помощью формулы Тейлора:
с
помощью формулы Тейлора:

т.е. ![]() и
тогда
и
тогда ![]() ,
а поскольку
,
а поскольку  ,
то
,
то
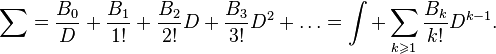
Применяя
это операторное соотношение к ![]() ,
получаем искомую формулу, но без
остаточного члена.
,
получаем искомую формулу, но без
остаточного члена.
Этот вывод чисто формальный и не касается вопросов сходимости.
Билет 20
20. Лоду с пос коэф. Второго порядка
Комплексные корни.
Случай различных диф корней характеристического уравнения.
Рассмотрим линейное дифференциальное уравнение вида
![]()
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:
![]()
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
![]()
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
![]()
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
![]()

51.представление ф-ции sin в виде ряда макларенса
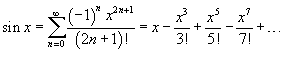
Билет21
21.Структура общего решения лнду второго порядка
Рассмотрим ЛНДУ второго порядка
![]()
где![]() -
заданные, непрерывные на (а;b) функции.
Уравнение
-
заданные, непрерывные на (а;b) функции.
Уравнение
![]()
левая часть которого совпадает с левой частью ЛНДУ (5.1), называется соответствующим ему однородным уравнением.
Теорема
5.1 (структура общего решения ЛНДУ). Общим
решением у уравнения (5.1) является сумма
его произвольного частного решения у*
и общего решения ![]() соответствующего
однородного уравнения (5.2), т. е.
соответствующего
однородного уравнения (5.2), т. е.
![]()
Убедимся,
что функция (5.3) - решение уравнения
(5.1). Так как у* есть решение уравнения
(5.1), а![]() -
решение уравнения (5.2), то
-
решение уравнения (5.2), то
![]()
В таком случае имеем:

Это
означает, что функция![]() является
решением уравнения (5.1).
является
решением уравнения (5.1).
Покажем теперь, что функция
![]()
является общим решением уравнения (5.1). Для этого надо доказать, что из решения (5.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям
![]()
Продифференцировав функцию (5.4) и подставив начальные условия (5.5) в функцию (5.4) и ее производную, получим систему уравнений:
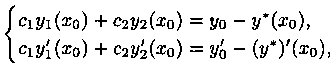
где
уо=у(хо),
у'0=y'(x0),
с неизвестными c1 и
с2.
Определителем этой системы является
определитель Вронского W(x0)
для функции y1(x)
и у2(х)
в точке х=хо.
Функции y1(x)
и у2(х)
линейно независимы (образуют фундаментальную
систему решений), т. е.![]() Следовательно,
система имеет единственное решение:
c1=с01 и
с2=с02.
Следовательно,
система имеет единственное решение:
c1=с01 и
с2=с02.
Решение![]() является
частным решением уравнения (5.1),
удовлетворяющим заданным начальным
условия
является
частным решением уравнения (5.1),
удовлетворяющим заданным начальным
условия
52.представление ф-ции cos в виде ряда макларенса
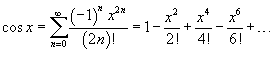
Билет22
22 решение общего решения лнду второго порядка методом лагранжа
непосредственное
нахождение частного решения лнду, кроме
случая уравнения с постоянными
коэффициентами, причем со специальными
свободными членами, представляет большие
трудности. Поэтому для нахождения общего
решения лнду обычно применяют метод
вариации произвольных постоянных,
который всегда дает возможность найти
общее решение лнду в квадратурах, если
известна фундаментальная система
решений соответствующего однородного
уравнения. Этот метод состоит в
следующем.
Согласно
вышеизложенному, общее решение линейного
однородного уравнения:
![]() ,
(8.1)
где
,
(8.1)
где ![]() –
линейно независимые на некотором
интервале X решения лоду, а
–
линейно независимые на некотором
интервале X решения лоду, а ![]() -
произвольные постоянные. Будем искать
частное решение лнду в форме (8.1), считая,
что
-
произвольные постоянные. Будем искать
частное решение лнду в форме (8.1), считая,
что ![]() –
не постоянные, а некоторые, пока
неизвестные, функции от
–
не постоянные, а некоторые, пока
неизвестные, функции от ![]() :
:
![]() .
(8.2)
Продифференцируем
равенство (8.2):
.
(8.2)
Продифференцируем
равенство (8.2):
![]() .
(8.3)
Подберем
функции
.
(8.3)
Подберем
функции ![]() и
и ![]() так,
чтобы выполнялось равенство:
так,
чтобы выполнялось равенство: ![]() .
Тогда вместо (8.3) будем иметь:
.
Тогда вместо (8.3) будем иметь:
![]() .
(8.4)
Продифференцируем
это выражение еще раз по
.
(8.4)
Продифференцируем
это выражение еще раз по ![]() .
В результате получим:
.
В результате получим:
![]() .
(8.5)
Подставим
(8.2), (8.4), (8.5) в лнду 2-го
порядка
.
(8.5)
Подставим
(8.2), (8.4), (8.5) в лнду 2-го
порядка ![]() f(x):
f(x):
![]() f(x)
или
f(x)
или
![]() f(x).
(8.6)
Так
как
f(x).
(8.6)
Так
как ![]() -
решения лоду
-
решения лоду ![]() ,
то последнее равенство (8.6) принимает
вид:
,
то последнее равенство (8.6) принимает
вид: ![]() f(x).
Таким
образом, функция (8.2) будет решением лнду
в том случае, если функции
f(x).
Таким
образом, функция (8.2) будет решением лнду
в том случае, если функции ![]() и
и ![]() удовлетворяют
системе уравнений:
удовлетворяют
системе уравнений:
![]() (8.7)
Так
как определителем этой системы является
определитель Вронского для двух линейно
независимых на X решений соответствующего
лоду, то он не обращается в ноль ни в
одной точке интервала X. Следовательно,
решая систему (8.7), найдем
(8.7)
Так
как определителем этой системы является
определитель Вронского для двух линейно
независимых на X решений соответствующего
лоду, то он не обращается в ноль ни в
одной точке интервала X. Следовательно,
решая систему (8.7), найдем ![]() и
и ![]() :
: ![]() и
и ![]() .
Интегрируя, получим:
.
Интегрируя, получим:
![]() ,
, ![]() ,
где
,
где ![]() -
произвольные постоянные.
Возвращаясь
в равенство (8.2), получим общее решение
неоднородного уравнения:
-
произвольные постоянные.
Возвращаясь
в равенство (8.2), получим общее решение
неоднородного уравнения:
![]() .
.
53.представление
ф-ции
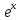 в
виде ряда макларенса
в
виде ряда макларенса
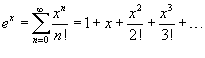
Билет23
23. лнду с пост коэффициентами с правой частью специального вида.
Общее решение yОН линейного неоднородного дифференциального уравнения L(y)=b(x) есть сумма общего решения yОО соответствующего однородного уравнения L(y) = 0 и какого - либо частного решения yЧН исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто.
Функцию 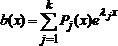 ,
где Pj(x)
- некоторые полиномы (многочлены), назовём
квазиполиномом. По теореме о наложении
решений, если yj ,
j=1,2,..,m - решения уравнений L(y) = bj(x),
то
,
где Pj(x)
- некоторые полиномы (многочлены), назовём
квазиполиномом. По теореме о наложении
решений, если yj ,
j=1,2,..,m - решения уравнений L(y) = bj(x),
то 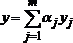 есть
решение уравнения
есть
решение уравнения  .
Поэтому, не умаляя общности, будем
считать, что правая часть уравнения
L(y) = b(x) с постоянными коэффициентами
имеет вид b(x) = P(x)eλx.
В частности, если λ=α+βi - комплексное
число, то наиболее общей правой частью
указанного типа является функция
.
Поэтому, не умаляя общности, будем
считать, что правая часть уравнения
L(y) = b(x) с постоянными коэффициентами
имеет вид b(x) = P(x)eλx.
В частности, если λ=α+βi - комплексное
число, то наиболее общей правой частью
указанного типа является функция
![]() (1)
(1)
у которой P(x)и Q(x)- некоторые полиномы. Справедлив следующий результат.
Теорема. Линейное дифференциальное уравнение
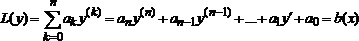
с постоянными коэффициентами и правой частью вида (1) имеет частное решение
![]() ,
,
где k - кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x) , S(x) - полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x) , Q(x).
