Тема 10

Лекции по математике. Тема 10

Страница 1

РАЗДЕЛ 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.

Тема 10. Статистическая проверка статистических гипотез.

•Статистические критерии.

•Ошибки первого и второго рода.

•Уровень значимости и мощность критерия.

•Параметрические и непараметрические критерии.

•Критерии значимости и их связь с интервальным оцениванием.

•Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

•Проверка гипотезы о распределении генеральной совокупности по биномиальному закону.

•Проверка гипотезы о равномерном распределении генеральной совокупности.

•Проверка гипотезы о распределении генеральной совокупности по показательному закону.

Статистические критерии.

Прежде чем перейти к рассмотрению понятия статистической гипотезы, сформулируем так называемый принцип практической уверенности, лежащий в основе применения выводов и рекомендаций с помощью теории вероятностей и математической статистики. «Если вероятность события А в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным в том, что событие А не произойдет, и в практической деятельности вести себя так, как будто событие А вообще невозможно».

Этот принцип не может быть доказан математически; он подтверждается всем практическим опытом человеческой деятельности, и мы постоянно (хотя и бессознательно) им руководствуемся. Например, отправляясь самолетом в другой город, мы не рассчитываем на возможность погибнуть в авиационной катастрофе, хотя некоторая (весьма малая) вероятность такого события все же имеется.

Обратим внимание на то, что принцип практической уверенности о невозможности маловероятных событий сформулирован «при однократном выполнении испытания». Если же произведено много испытаний, в каждом из которых вероятность события А даже очень мала, то существенно повышается вероятность того, что событие А произойдет хотя бы один раз в массе испытаний. Действительно, пусть вероятность Р(А) = α , где α << 1. Тогда вероятность события В, состоящего в том, что событие А произойдет хотя бы один раз в п независимых испытаниях, равна (при α << 1):

P(B) =1 −(1 −α)n ≈1 −(1 −nα) = nα ,

т.е. вероятность Р(В) увеличилась по сравнению с Р(А) в n раз.

Таким образом, при многократном повторении испытаний мы уже не можем считать маловероятное событие А практически невозможным.

Вопрос о том, насколько мала должна быть вероятность α события А, чтобы его можно было считать практически невозможным, выходит за рамки математической теории и решается в каждом отдельном случае с учетом важности последствий, вытекающих из наступления события А. В одних случаях считается возможным пренебрегать событиями, имеющими вероятность меньше 0,05, а в других, когда речь идет, например, о разрушении сооружений, гибели судна и т.п., нельзя пренебрегать событиями, которые могут появиться с вероятностью, равной 0,001.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 2

С теорией статистического оценивания параметров тесно связана проверка статистических гипотез. Она используется всякий раз, когда необходим обоснованный вывод о преимуществах того или иного способа инвестиций, измерений, стрельбы, технологического процесса, об эффективности нового метода обучения, управления, о пользе вносимого удобрения, лекарства, об уровне доходности ценных бумаг, о значимости математической модели и т.д.

Под статистическими гипотезами подразумеваются такие гипотезы, которые относятся или к виду случайной величины, или к отдельным параметрам распределения случайной величины.

К статистическим гипотезам можно отнести высказывания типа:

o «Случайная величина Х подчиняется нормальному закону распределения»;

o «Генеральные средние двух исследуемых совокупностей равны между собой».

Так, например, статистической является гипотеза о том, что распределение трудовых ресурсов в одинаковых организационно-технических условиях имеет нормальный закон распределения. Статистической будет также гипотеза о том, что средние размеры одежды, производимые на однотипных предприятиях, не различаются между собой.

Различают простую и сложную статистические гипотезы. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения случайной величины. Простой (сложной) называют гипотезу, содержащую одно (несколько) предположение (предположений).

Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают H0. Наряду с нулевой гипотезой H0 рассматривают альтернативную, или конкурирующую, гипотезу H1, являющуюся логическим отрицанием H0. Нулевая и альтернативная гипотезы представляют собой две возможности выбора, осуществляемого в задачах проверки статистических гипотез.

Обычно в качестве нулевой гипотезы используется простая гипотеза. Например, в качестве нулевой гипотезы можно использовать следующие высказывания:

o«Стоимость потребительской корзины жителей Ульяновской области составляет 6450 рублей в месяц»;

o«Время на выполнение одной из операций при изготовлении детали равно четырем минутам»;

o «Доля нетрудоспособного населения в области составляет 8% от общей численности».

Таким образом, перед нами стоит задача проверки гипотезы H0 относительно конкурирующей гипотезы H1. Проверка производится на основании данных выборочных исследований, состоящих из n независимых наблюдений X1,.., X n над случайной

величиной Х.

Статистическим критерием называют правило, которое позволяет оценить меру расхождения результатов, полученных при оценке выборочного наблюдения и основной выдвинутой гипотезы H0.

Статистическим критерием также называют случайную величину К, служащую для проверки нулевой гипотезы.

Ошибки первого и второго рода.

Возможные значения случайной величины Х могут быть разделены на два непересекающихся подмножества – критическую область и область принятия гипотезы.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 3

Областью принятия гипотезы (областью допустимых значений) О называют совокупность значений критерия, при которых эту гипотезу Н0 принимают.

Критической областью (областью отклонения гипотезы) W для данного статистического критерия называют множество значений критерия, при которых нулевую гипотезу Н0 отвергают.

Критерий К позволяет при заданном уровне значимости определить критическую точку Kкр , которая разделяет область значений критерия на две части: область допустимых

значений О, в которой результаты выборочного исследования выглядят более правдоподобно, и критическую область W, в которой результаты выборочного наблюдения менее правдоподобны в отношении гипотезы Н0 . Обычно Kкр определяется

по таблице соответствующего распределения.

Так как подмножество О состоит из тех выборок, которые не вошли в подмножество W, то подмножество W однозначно определяет подмножество О, и наоборот, т.е. необходимо определить одно подмножество, второе же получается автоматически единственным образом.

Возникает вопрос о том, какими принципами следует руководствоваться при построении критической области W. Эти принципы были сформулированы в работах известных математиков Е.Неймана и Э.Пирсона.

Поскольку результатом исследования гипотезы служит управленческое решение, необходимо в ситуации неопределенности знать последствия возможных ошибок.

Возможны следующие ошибки:

•Отвергнута нулевая гипотеза Н0 , а принята гипотеза Н1 , в то время как в действительности все же верна гипотеза Н0 - ошибка первого рода;

•Принимается нулевая гипотеза Н0 , в то время как верна гипотеза Н1 - ошибка второго рода.

Рассмотренные случаи наглядно иллюстрирует следующая таблица:

Гипотеза Н0	Принимается	Отвергается
Верна	Правильное решение	Ошибка 1-го рода
Неверна	Ошибка 2-го рода	Правильное решение

Уровень значимости и мощность критерия.

Вероятности ошибок первого и второго рода однозначно определяются выбором критической области W. Для любой заданной критической области W условимся обозначать через α вероятность ошибки первого рода (уровень значимости), через β -

вероятность ошибки второго рода. Ошибки первого рода также называют α -риском, а ошибки второго рода принято называть β -риском.

При фиксированном объеме выборки принято задавать вероятность ошибки первого рода α =1 −γ , где γ - вероятность значимости гипотезы Н0 . Если вероятность, с которой мы

хотим определить достоверность предположения Н0 , γ =0,95, то уровень значимости

равен 0,05. Обычно (в таблицах для конкретных видов распределения) уровень значимости α задается некоторыми стандартными значениями: 0,05; 0,01; 0,005; 0,001.

Вероятность (1− β) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н0 , когда она неверна, называется мощностью критерия.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 4

Пользуясь терминологией статистического контроля качества продукции, можно сказать, что вероятность α представляет «риск поставщика», связанный с забраковкой по результатам выборочного контроля изделий всей партии, удовлетворяющей стандарту, а вероятность β — «риск потребителя», связанный с принятием по анализу выборки

партии, не удовлетворяющей стандарту.

Применяя юридическую терминологию, α - вероятность вынесения судом обвинительного приговора, когда на самом деле обвиняемый невиновен, β —

вероятность вынесения судом оправдательного приговора, когда на самом деле обвиняемый виновен в совершении преступления. В ряде прикладных исследований ошибка первого рода α означает вероятность того, что предназначавшийся наблюдателю сигнал не будет им принят, а ошибка второго рода β — вероятность того, что

наблюдатель примет ложный сигнал.

Вероятности ошибок 1-го и 2-го рода (α и β ) однозначно определяются выбором критической области. Очевидно, желательно сделать как угодно малыми α и β . Однако

это противоречивые требования: при фиксированном объеме выборки можно сделать как угодно малой лишь одну из величин — α или β , что сопряжено с неизбежным

увеличением другой. Лишь при увеличении объема выборки возможно одновременное уменьшение вероятностей α и β .

На бытовом уровне ошибки второго рода (ошибки потребителя) могут иметь более трагические последствия, чем ошибки первого рода. Говорят: ошибки первого рода – ошибки осторожных людей, ошибки второго рода – пропуск брака – порой лихачество.

Параметрические и непараметрические критерии.

Различают три вида критериев:

1.Параметрические критерии – критерии значимости, которые служат для проверки гипотез о параметрах распределения генеральной совокупности.

2.Критерии согласия позволяют проверять гипотезы о соответствии распределений генеральной совокупности известной теоретической модели.

3.Непараметрические критерии используют в гипотезах, когда не требуется знаний о конкретном виде распределений.

Критерии значимости и их связь с интервальным оцениванием.

Значение критерия на основе выборочного наблюдения определяется по специальным правилам и называется наблюдаемым значением критерия Kнабл .

Если наблюдаемое значение критерия Kнабл попадает в область допустимых значений О,

значит, на основе выборочных данных на принятом уровне значимости можно принять нулевую гипотезу Н0 как более правдоподобную для результатов выборочного

исследования, и отклонить альтернативную.

Если же наблюдаемое значение критерия попадает в критическую область W, то нулевая гипотеза отклоняется в пользу альтернативной гипотезы Н1 .

В зависимости от содержания альтернативной гипотезы Н1 осуществляется выбор критической области: левосторонней, правосторонней или двусторонней в зависимости от того, как задана конкурирующая гипотеза Н1 .

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 5

Если смысл исследования заключается в доказательстве конкретного изменения наблюдаемого параметра (его уменьшения или увеличения) то говорят об односторонней критической области.

Если смысл исследования – выявить различия в изучаемых параметрах, но характер их отклонений от контрольных (или теоретических) не известен, то говорят о двусторонней критической области или двусторонних критериях.

Выбор критерия осуществляется до начала эксперимента, но важно учесть, что более точные результаты дают односторонние критерии.

Как уже говорилось ранее, границы критической области – значения критерия Kкр -

определяют с помощью уровня значимости α и предположения о характере распределения соответствующей статистики:

Критическая	Определение критической				Значение Ккр через α
область W		области
Левосторонняя		Kнабл < Kкр			P(Кнабл < Ккр ) =α
Правосторонняя		Kнабл > Ккр			P(Кнабл > Ккр ) =α
Двусторонняя	Кнабл < Ккр , Кнабл > −Ккр или				P(Кнабл < Ккр ) = P(Кнабл > −Ккр ) =α / 2
симметричная		Кнабл		> Ккр

В том случае, когда конкурирующая гипотеза Н1 - правосторонняя, то и критическая область – правосторонняя. Тогда, если Kнабл попадает в интервал от - ∞до Kкр , то нулевая гипотеза принимается, а альтернативная отклоняется. Если же Kнабл > Ккр , то нулевая гипотеза отклоняется в пользу альтернативной.

В том случае, когда конкурирующая гипотеза Н1 левосторонняя, то и критическая область левосторонняя. Тогда, если Kнабл лежит в интервале от - ∞до Kкр , то нулевая гипотеза отклоняется в пользу альтернативной. Если же Kнабл > Ккр , то нулевая гипотеза принимается, а альтернативная отклоняется.

Если конкурирующая гипотеза Н1 двусторонняя, то и критическая область двусторонняя. Тогда нулевая гипотеза принимается, если − Ккр < Kнабл < Kкр , и отклоняется в противном случае в пользу альтернативной.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 6

Однако принятие той или иной гипотезы не дает оснований утверждать, что она верна, так как один положительный результат не может служить основанием для того, чтобы считать некоторое утверждение достоверным. Так, в процессе сбора и обработки экспериментальных данных могли появиться ошибки по различным причинам, мог оказаться недостаточным объем эмпирических данных и т.д. Результаты проверки статистической гипотезы лишь устанавливают на определенном уровне значимости α ее

соответствие (несоответствие) результатам эксперимента.

Алгоритм проверки статистических гипотез.

Проверку статистической гипотезы можно осуществить по следующему алгоритму:

1. Сформулировать основную Н0 и альтернативную Н1 гипотезы в вероятностных

терминах на основе выборочных данных и в зависимости от цели исследования.

2. Выбрать соответствующий уровень значимости критерия, обычно

α{0,001;0,05;0,01;0,1} .

3.Определить (если он не задан) объем выборки n и число степеней свободы k.

4.Подобрать наиболее мощный критерий оценки гипотезы по статистическим данным. Чаще всего это:

и– нормальное распределение;

χ2 - распределение Пирсона хи-квадрат; t – распределение Стьюдента;

F– распределение Фишера-Снедекора.

5.Вычислить экспериментальное значение критерия Kнабл на основе выборочных данных.

6.Определить табличное значение критерия Kкр , которое отделяет критическую область W от области допустимых значений. В зависимости от вида альтернативной гипотезы в

соответствующей таблице выбирают квантили критерия для двусторонней ( K1−α / 2 и Kα / 2 ) или односторонней области ( K1−α и Kα ).

7.Если значение Kнабл находится в области допустимых значений, то на уровне значимости α нулевая гипотеза принимается, а конкурирующая отклоняется.

8.Если вычисленное по выборочным данным значение Kнабл попадает в критическую область, то нулевая гипотеза отклоняется в пользу конкурирующей гипотезы.

Заметим, что вероятность принятия гипотезы Н0 основана на принципе практической

невозможности наступления маловероятных событий (принципе практической уверенности).

Легко показать, что, отыскивая двустороннюю критическую область при уровне значимости α , тем самым находят и соответствующий доверительный интервал с надежностью γ =1 −α . Но, хотя отыскание двусторонней критической области и

доверительного интервала приводит к одинаковым результатам, их истолкование различно: двустороння критическая область определяет границы (критические точки), между которыми заключено (1-α )% числа наблюдаемых критериев, найденных при повторении опытов; доверительный же интервал определяет границы (концы интервала), между которыми в γ = (1 −α) % опытов заключено истинное значение оцениваемого

параметра.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 7

Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

Если закон распределения неизвестен, но есть основания предположить, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится так же, как и проверка гипотезы о параметрах распределения, т.е. при помощи специально подобранной случайной величины – критерия согласия.

Имеется несколько критериев согласия: χ2 («хи-квадрат») Пирсона, Колмогорова,

Смирнова и др. Рассмотрим описание применения критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности. С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты.

Эмпирические и выравнивающие частоты.

Дискретное распределение. Рассмотрим дискретную случайную величину Х, закон распределения которой неизвестен. Пусть произведено n испытаний, в которых величина

Х приняла n1 раз значение x1 ,…, nk раз значение xk , причем ∑ni = n .

Эмпирическими частотами называют фактически наблюдаемые частоты ni .

Выравнивающими в отличие от фактически наблюдаемых эмпирических частот называют частоты ni′, найденные теоретически (вычислением) по формуле ni′ = n Pi , где n – число

опытов, Pi - вероятность наблюдаемого значения xi , вычисленная при допущении, что Х имеет предполагаемое распределение.

Непрерывное распределение. В случае непрерывного распределения вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности Pi

попадания Х в i-й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности.

В частности, если имеются основания предположить, что случайная величина Х (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле:

ni′ = σnh ϕ(ui ) ,

B

где n – число испытаний (объем выборки), h – длина частичного интервала, σB -

выборочное среднее квадратическое отклонение, ui			=	xi − xB	( xi - середина i-го
частичного интервала),				σB
	1
ϕ(u) =		e−u2 / 2 .
	2π

Для того чтобы наглядно увидеть различие эмпирических и теоретических частот, рассмотрим пример на построение нормальной кривой по опытным данным.

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10												Страница 8
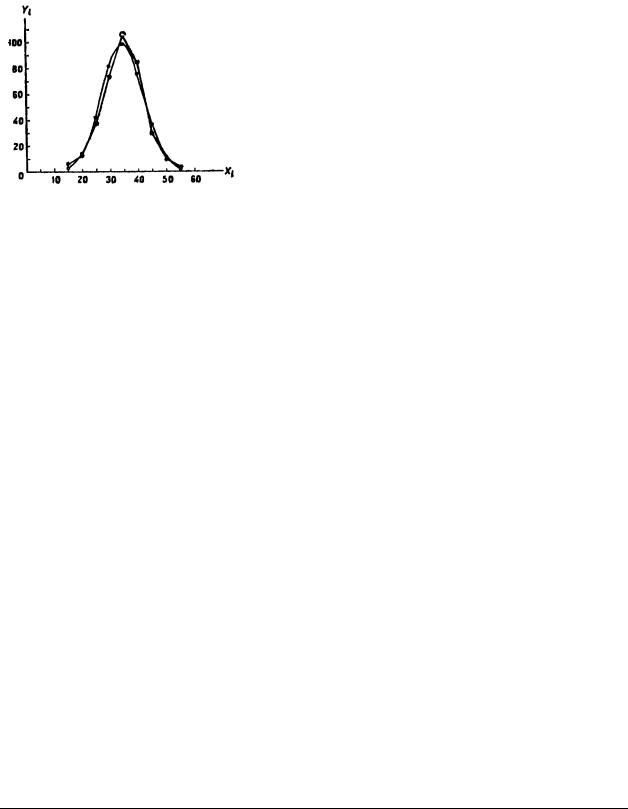
Пример 1. Построить нормальную кривую по данному распределению:
	варианты	xi	15	20	25	30	35	40	45	50	55
	частоты	ni	6	13	38	74	106	85	30	10	4

Решение. Один из способов построения нормальной кривой по данным наблюдений состоит в следующем:

1.Находят xB =34,7 и σB =7,38.

2.Находят ординаты yi (выравнивающие частоты) теоретической кривой по формуле

yi = nh ϕ(ui ) , для чего заполним таблицу (см. Приложение 1):

σB

			ui =	x	− x				ϕ(ui )	yi =	nh		ϕ(ui ) = 248	ϕ(ui )
xi	ni	xi − xB			i		B
											σ
					σ	B						B
15	6	-19,7	-2,67						0,0113				3
20	13	-14,7	-1,99						0,0551				14
25	38	-9,7	-1,31						0,1691				42
30	74	-4,7	-0,63						0,3271				82
35	106	0,3	0,05						0,3984				99
40	85	5,3	0,73						0,3056				76
45	30	10,3	1,41						0,7476				37
50	10	15,3	2,09						0,0449				11
55	4	20,3	2,77						0,0086				2
	n=366											∑yi = 366

3. Строят точки ( xi , yi ) в прямоугольной системе координат и соединяют их плавной кривой.

На рисунке построены нормальная (теорическая) кривая по выравнивающим частотам (они отмечены кружками) и полигон наблюдаемых частот (они отмечены крестиками). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

Для того чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами (их называют критериями согласия).

Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос. Правда, как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает на принятом уровне значимости ее согласие или несогласие с данными наблюдений.

Итак, пусть по выборке объема n получено эмпирическое распределение:

варианты	xi	x1	x2	…	xs
эмп. частоты	ni	n1	n2	…	ns

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10 Страница 9

Допустим, что в предположении нормального распределения генеральной совокупности вычислены теоретические частоты ni′. При уровне значимости α требуется проверить

нулевую гипотезу: генеральная совокупность распределена нормально.

В качестве критерия проверки нулевой гипотезы примем случайную величину

χ2 = ∑(ni −ni )2 / ni′ . (*)

Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (*), и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Заметим, что возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. Делением на ni′ достигают

уменьшения каждого из слагаемых; в противном случае сумма была бы настолько велика, что приводила бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива.

Доказано, что при n → ∞ закон распределения случайной величины (*) независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ2 с k степенями свободы. Поэтому случайная величина (*)

обозначена через χ2 , а сам критерий называют критерием согласия «хи квадрат».

Число степеней свободы находят по равенству k = s −1 −r , где s – число групп (частичных интервалов) выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки.

В частности, если предполагаемое распределение – нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому r=2 и число степеней свободы k = s −1 −r =s-1-2=s-3.

Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр λ , поэтому r=1 и k=s-2.

Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α :

	P[χ2 > χкр2 (α; k)]=α .
Таким	образом, правосторонняя критическая область	определяется	неравенством
χ2 > χкр2	(α; k) , а область принятия нулевой гипотезы – неравенством χ2 < χкр2 (α; k) .
Обозначим значение критерия, вычисленное по данным		наблюдений,	через χнабл2 и
сформулируем правило проверки нулевой гипотезы.

Правило. [1] Для того чтобы при заданном уровне значимости проверить нулевую гипотезу Н0: генеральная совокупность распределена нормально, надо:

1.Вычислить теоретические частоты;

2.Вычислить наблюдаемое значение критерия:

χнабл2 = ∑(ni −ni′)2 / ni (**)

Для контроля вычислений формулу (**) преобразуют к виду

χнабл2 = [∑ni2 / ni′]−n .

3.По таблице критических точек распределения χ2 , по заданному уровню значимости

αи числу степеней свободы k = s −3 найти критическую точку χкр2 (α; k) .

Дмитриева М.В.

Редакция 31.08.2010

Лекции по математике. Тема 10

Страница 10

4.Если χ2 < χкр2 (α; k) - нет оснований отвергнуть нулевую гипотезу.

5.Если χ2 > χкр2 (α; k) - нулевую гипотезу отвергают.

Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.

Пример 2. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты (см. пример 1):

			эмп. частоты								6		13			38		74			106	85	30			14
			теорет. частоты								3		14			42		82			99	76	37			13
Решение. Вычислим χнабл2 , для чего составим расчетную таблицу:
	i		n	i	n′		n	i	−n′			(n		i	−n′)2			(n	i	−n′)2		/ n′		n2				n2	/ n′
					i					i						i					i	i			i			i	i
	1	6			3		3					9						3						36				12
	2	13			14		-1					1						0,07						169				12,07
	3	38			42		-4					16						0,38						1444				34,38
	4	74			82		-8					64						0,78						5476				66,78
	5	106			99		7					49						0,49						11236				113,49
	6	85			76		9					81						1,07						7225				95,07
	7	30			37		-7					49						1,32						900				24,32
	8	14			13		1					1						0,08						196				15,08
	∑	366			366													χнабл2 =4,44										373,19
По таблице критических						точек				распределения								χ2			(см. Приложение								4), по уровню

значимости α =0,05 и числу степеней свободы k =5 находим χкр2 (0,05; 5)=11,1.

Так как χнабл2 < χкр2 - нет оснований отвергнуть нулевую гипотезу. Другими словами,

расхождение эмпирических и теоретических частот незначимое. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

Проверка гипотезы о распределении генеральной совокупности по биномиальному закону.

Произведено n опытов. Каждый опыт состоит из N независимых испытаний, в каждом из которых вероятность появления события А одна и та же. Регистрируется число появлений события А в каждом опыте. В итоге получено следующее распределение дискретной случайной величины Х – числа появлений события А (в первой строке указано число xi

появлений события А в одном опыте; во второй строке – частота ni , т.е. число опытов, в которых зарегистрировано появлений события А):

xi	0	1	2	…	N
ni	0	1	2	…	nN

Требуется, используя критерий Пирсона, проверить гипотезу о распределении дискретной случайной величины Х по биномиальному закону.

Правило.[7] Для того чтобы при уровне значимости α проверить гипотезу о том, что дискретная случайная величина Х (число появлений события А) распределена по биномиальному закону, надо:

Дмитриева М.В.

Редакция 31.08.2010