Лекция № 10 Приближение функций и их производных.

1. Постановка задачи приближения функций.

Простейшая задача приближения функций заключается в следующем.

Пусть известны значения некоторой функции f(x) при заданных x₀ <x₁ < <x_n на некотором отрезке [x₀ , x_n]. Требуется получить значения f(x) для такого значения аргумента x, которое не входит в отрезок [x₀ , x_n ]., нo и не совпадает ни с одним из значений x_i, i=0, ,n

x	x0	x1		xn
f(x)	f0	f1		fn

При этом основная цель интерполяции получить быстрый и экономичный алгоритм вычисления значений функции F(x), для значений x не содержащихся в исходной таблице, т.е. xÎ[a, b] и x¹x_i.

f(x) @ F(x, a₀, a₁,…, a_n)

Параметры a₀, a₁,…, a_n - определяются из условий совпадения f(x) и приближающей функции в точках x₀ , x₁ , , x_n - узлах интерполяции

F(x_i, a₀, a₁,…, a_n) = f(x_i), i = 0, , n

Такой способ называется интерполированием.

Далее будем рассматривать задачу интерполирования многочленами, но это не единственный способ. Иногда удобнее приближать функцию тригонометрическими функциями или ln(f(x)). Интерполяционный многочлен Лагранжа.

На практике применяют аналитический способ нахождения коэффициентов a_j , применяя другой способ записи многочлена.

Определим - символ Кронекера.

Задача интерполирования будет решена, если мы построим такие многочлены F_i(x) степени не выше n, такие, что .

Тогда многочлен будет искомым интерполяционным многочленом. Действительно,

Кроме того, F_n - многочлен степени n .

Поскольку обращается в ноль в точкахx₀ , x₁ , ,x_n в n точках, то F_i(x) делится на (x-x_j)

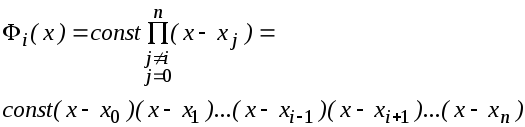
Из условия находим, что

и тогда ,

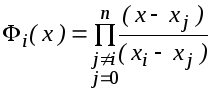тогда искомый многочлен имеет вид

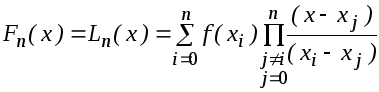
Называется интерполяционным многочленом Лагранжа.

Существуют другие формы записи интерполяционного многочлена, Формула Ньютона и ее варианты. Этим вариантам записи соответствует различие в величине вычислительной погрешности, а также различное количество арифметических операций.

Покажем единственность полинома Лагранжа.

Предположим обратное, пусть - полином степени не вышеn и

Тогда полином - обращается в нуль в(n+1) точках x₀ , x₁ , ,x_n и степени не выше n, т.е.

По следствию из основной теоремы алгебры многочленов – многочлен n –ой степени не может иметь более n корней.

Формуле Лагранжа можно придать более сжатый вид:

Дифференцируя по х это произведение, получим:

При x=x_i

Отсюда, получаем

Замечание. Нетрудно оценить число арифметических действий, в главном порядке по n это есть величина O(n²).

Рассмотрим 2 частных случая интерполяционного полинома Лагранжа.

При n =1 имеем 2 узла и формула L_n представляет собой уравнение прямой, проходящей через 2 заданные точки:

При n =2 получим уравнение параболы L₂(x), проходящей через 3 точки:

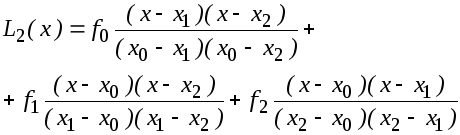
L₁(x) и L₂(x), называются соответственно формулами линейной и квадратичной интерполяции.