Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновское Высшее Авиационное Училище Гражданской Авиации

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Часть 2. Однофакторная регрессия

.pdf

Скачиваний:

Добавлен:

20.04.2015

Размер:

321.38 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

Тема 2. Регрессия МНК с одной объясняющей переменной.

Математические свойства оценок МНК......................................................................................	1
Статистические свойства оценок МНК. Теорема Гаусса-Маркова..........................................	5

Проверка гипотез и построение доверительных интервалов в регрессии с нормальными

ошибками..........................................................................................................................	11
Литература по однофакторной регрессии.................................................................................	16

Уравнение регрессии представляет собой линейную зависимость объясняемой переменной (regressand) от объясняющих переменных (regressors). Для простоты мы сначала рассмотрим случай одной объясняющей переменной, тогда уравнение регрессии

будет иметь вид:	Yi	=α + β Xi + ei
(2.01)	Yi	=α + β Xi + ei
где Yi -объясняемая	переменная,	Xi - объясняющая, ei -ошибка. Индекс i =1........	N -

означает, что у нас есть N пар значений X и Y , по которым мы и оцениваем уравнение регрессии. Линейный метод наименьших квадратов состоит в том, что коэффициенты α и β в уравнении (2.01) выбираются так, чтобы сумма квадратов ошибок была минимальна:

	N		N
(2.02)	∑ei	2	=∑(Yi −α − β Xi )2 min
	i =1		i=1	α, β

Обычно слово линейный опускают и называют его метод наименьших квадратов сокращенно МНК, в англо язычной литературе он называется (ordinary least squares сокращенно OLS). Линейным метод называется, так как уравнение (2.01) линейно по параметрам α и β .

МНК является одним из трех основных методов, которые используются для оценки эконометрических уравнений. Другие два, это метод максимального правдоподобия и метод моментов. Широкое использование МНК объясняется тем, что полученные с его помощью оценки обладают рядом хороших свойств. Рассмотрим эти свойства более подробно.

Математические свойства оценок МНК.

Свойства, которые мы сейчас рассмотрим, вытекают непосредственно из формул, по которым вычисляются оценки МНК. Поэтому для их выполнения не важно откуда мы получили X и Y , по которым мы оцениваем регрессию. То есть X и Y могут быть как просто набором детерминированных чисел, так и выборкой из случайных величин с произвольной функцией распределения.

Выведем формулы оценок МНК, для этого нужно решить задачу (2.02). Необходимые условия будут иметь вид:

	N
	∂∑(Yi −α − β Xi )2	N	N
	i =1	= −2 ∑(Yi −α − β Xi )= ∑ei = 0
	∂α
(2.03)		i =1	i=1
	N

	∂∑(Yi −α − β Xi )2	N	N
	i =1	= −2 Xi ∑(Yi −α − β Xi )= ∑Xi ei = 0

	∂β
		i =1	i=1

(2.03) обычно называют системой нормальных уравнений. Решая эту систему, мы получаем формулы оценок коэффициентов

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

)

∑Xi Yi − N X Y

i=1

(2.04)

− N X

∑Xi

)

i=1)

=Y −β

∑(Xi − X ) (Yi −Y )

= i=1

∑(Xi − X )2

i=1

=	∑xi	yi	=	cov (X ,Y )
	∑xi2			D (X )

где yi =Yi −Y xi = Xi − X .

Чтобы убедится, что найденная нами точка экстремума суммы квадратов ошибок является именно точкой минимума, а не максимума проверим достаточные условия, для этого вычислим вторые производные и проверим положительную определенность матрицы Гессе.

∂2 ∑(Yi −α − β Xi )2

i=1		= 2 N ;
i=1
	∂α2

∂2 ∑(Yi −α − β Xi )2

i=1

∂α∂β

2 N H = N2∑X

i=1 i

2 N ≥ 0

	2∑Xi
	N
	i =1
	N
	N
	2∑Xi2
	i =1

=2∑Xi

i=1N

N
∂2 ∑(Yi −α − β Xi )2			N
i=1			= 2∑Xi2 ;
	∂β	2	= 2∑Xi2 ;
	∂β		i=1

det H = 4

∑Xi

∑Xi2 − N X 2

= 4 N ∑(Xi − X )

≥ 0

∑Xi2 −

= 4

i=1

Матрица Гессе положительно определена, мы действительно нашли минимум.

Используя оценки α

и β),

можно получить вектор МНК оценок объясняемой

переменной или предсказанных значений:

)

(2.05)

)

=α + β X

и вектор МНК оценок ошибок:

)

(2.06)

e =Y −Y

=Y −α − β X

Непосредственно из (2.04), (2.05) и (2.06) вытекают следующие свойства оценок

МНК.

1) ∑ei

= 0 из (2.03)

i =1

2) ∑Xi ei = 0 из (2.03)

i =1

N )

3) ∑Yi

= 0 из (2.05) и свойств 1 и 2.

i =1

N )

∑Yi

i=1

i =1

- предсказанное среднее и выборочное среднее равны из (2.06) и

свойства 1.

)

всегда проходит через точку

5) Y =α + β X то есть линия регрессии Y

=α + β X

) из (2.04).

, Y

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

6) Сумма квадратов отклонений от среднего объясняемой переменной может быть представлена как:

(2.07)	∑(Yi −Y )2	=∑(Y)i	−Y )2 +∑ei2
	N	N		N
	i =1	i=1		i=1

из (2.06) и свойств 3 и 4.

Внимание! если из уравнения регрессии (2.05) исключить коэффициент α , то есть оценивать модель Y)i = β) Xi , то справедливыми останутся только свойства 2 и 3. Все остальные будут не верны!

Задача на дом №1. Найдите формулу МНК оценки β) для модели Y)i = β) Xi и

проверьте, что для этой модели выполняются только свойства 2 и 3.

Рассмотрим более подробно свойство 6, иногда его называют геометрической

теоремой

Пифагора.

Сначала

поймем,

как

его

доказать.

Из

(2.06)

Yi =Yi

+ ei ,

соответственно Y 2

=Y 2

+ 2Y) e + e2 , суммируя по N , получаем:

)

(2.08)

∑Yi

2 =∑Yi 2 +∑ei2

i =1

i=1

i =1

)

так как ∑Yi ei = 0 . Рассмотрим,

что это означает с точки зрения геометрии. У нас есть

i =1

N -мерные векторы

Y)1

Y =

Y) = Y)

X = X

e = e

i = 1

)

X N

)

Из 2.05 мы знаем, что Y

является линейной комбинацией векторов X

и i : Y

=α i

+ β X

поэтому вектор Y

лежит в той же плоскости, что и вектора X

и i . Так же знаем, что

скалярные

произведения векторов

i,e = 0 ,

так

как

∑ei = 0 ,

X , e = 0 ,

так

как

i=1

∑Xi ei = 0 ,

значит вектор e

ортогонален (или перпендикулярен)

векторам

i , а

i =1

соответственно и

плоскости,

которой

эти

два вектора

лежат.

Поэтому

он

также

)

ei = 0 , то есть

)

ортогонален вектору Y ,

в этом и состоит свойство 3: ∑Yi

= 0 . В

i =1

свою очередь Y =Y +e ,

поэтому вектора Y , Y ,e образуют прямоугольный треугольник и

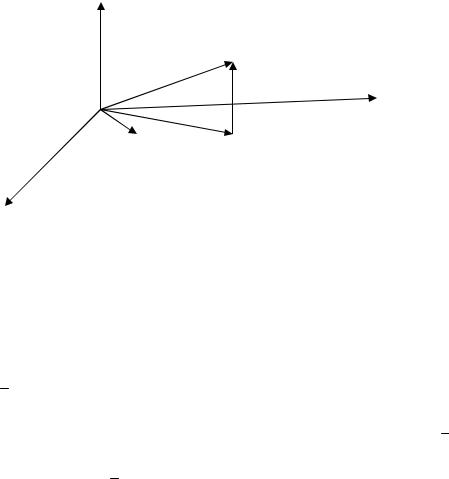
для их длин выполняется теорема Пифагора, что и записано в (2.08). (Если вы еще

помните, длинна вектора это корень из суммы квадратов его компонент). Вектор Y является проекцией вектора Y на плоскость образованную векторами X и i . Соответственно вектор e это нормаль (перпендикуляр) проведенная к этой плоскости. Поэтому (2.03) и называют системой нормальных уравнений. Графически это изображено на рисунке 1.

Он мне все равно не нравится, хотя я его и долго рисовал, может попробую потом еще переделать его. У вас не должно складывается впечатление, что мы строим проекцию из трех мерного пространства в двумерное. Дело в том, что плоскость образованная векторами X и i никогда не будет совпадать с плоскостью образованной двумя осями координат, как у меня здесь получилось, да и пространство должно быть N -мерное.

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

Y e

X i Y

Чтобы доказать свойство 6 нам осталось в (2.08) от суммы квадратов перейти к

сумме квадратов отклонений от среднего. Так как ∑ei = 0 и средние значения

i =1

наблюдаемых и предсказанных игреков у нас совпадают, то из (2.08) получаем:

N )

∑Yi 2 + N Y

2 =∑Yi

2 + N Y 2 −2∑ei +∑ei2 ,

i=1

∑Yi

=∑Y)i

2 −2∑(Yi −Y)i )

+∑ei2 выделяя нужные нам полные квадраты

2 + N Y

i=1

разностей ∑(Yi −Y

)2 =∑(Y)i

+∑ei2

- это и есть свойство 6, которое мы доказывали.

−Y

i =1

i=1

Равенство (2.07) часто записывают, как TSS = ESS + RSS , где TSS = ∑(Yi −Y

)2 -

i=1

total sum of squares, ESS = ∑(Y)i −Y

)2 -explained sum of squares, RSS = ∑ei2 residual sum of

i=1

squares. Некоторые полезные утверждение относительно TSS, ESS, RSS, β). Перейдем к

yi =Yi

−Y , xi

= Xi

− X , тогда TSS = ∑yi2 ,

β) = ∑xi 2yi

)

i=1

)

∑xi

)

∑ i

∑( i

i )

{

}

∑

( i

i )

RSS =

−α −β X

α =Y

−β X

Y −Y

+ β X −β X

(2.09)

i=1

= ∑yi2

−2β)

∑yi xi

+ β)

2 ∑xi2

i=1

−2 ∑xi 2yi ∑yi xi

= ∑(yi −β) xi )2

= ∑yi2

i=1

∑xi

i=1

∑xi yi

(∑xi yi )2

)

∑xi

= ∑yi −

= ∑yi

−β ∑yi xi

∑xi

i=1

∑xi

i=1

)

(2.10)

ESS =TSS − RSS = ∑yi2 −∑yi2 + β ∑yi xi = β ∑yi xi

i=1

Коэффициент R2 определяется как

(2.11)

ESS

=1−

RSS

TSS

R2 является мерой качества регрессии, он показывает долю общей дисперсии переменной Y , которую удалось объяснить с помощью переменной X . Он так же называется коэффициентом детерминации. Коэффициент детерминации показывает степень тесноты статистической связи между результирующим показателем и набором объясняющих

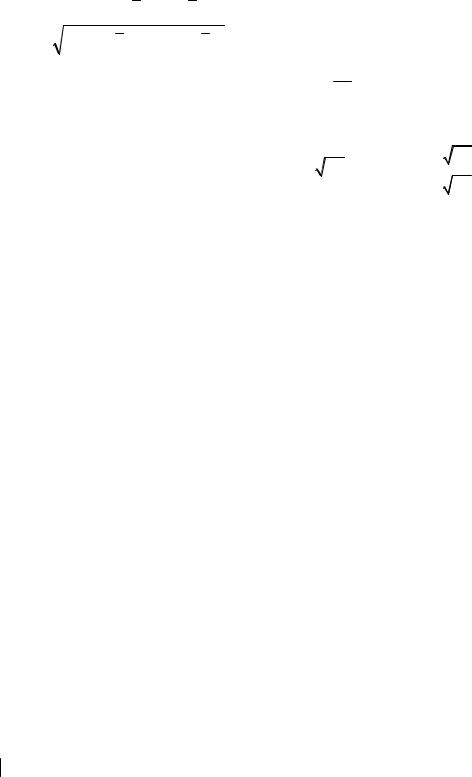
Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

факторов. R2 -это формула его вычисления в рассматриваемом нами случае, когда

зависимость линейная. Коэффициент R2 по определению меняется от 0 до 1. Подставляя (2.10) и (2.04) в (2.11) получаем:

ESS

)

∑yi xi

i=1

(2.12)

= β

i 1

= r2 (X ,Y ),

TSS

∑yi2

∑xi2 ∑yi2

∑(X − X

) (Y −Y

)

i=1

i=1 i=1

где r (Y , X )=

-выборочный

коэффициент

корреляции между

∑(Y −Y

)2 ∑(X − X

)

переменными

X ,Y . Так как Yi

=α + β

, то

r (Y ,Y )=

)

r (X ,Y ). Соответственно

(2.13)

= r2 (Y),Y )= r2 (X ,Y )

)

Задачка на дом №2. Покажите, что

, r (X ,Y )=

β > 0

r (Y ,Y )= + R2

)

−

β < 0

Статистические свойства оценок МНК. Теорема ГауссаМаркова.

В этой главе мы посмотрим, какими свойствами обладают МНК оценки модели регрессии, когда по имеющейся у нас выборке размера N мы оцениваем параметры существующей в генеральной совокупности линейной зависимости:

(2.14) Yi =α +β Xi +εi

Я начну с того, что приведу основной результат. Теорема Гаусса-Маркова. Если

1)Модель правильно специфицирована, то есть зависимость вида (2.14) действительно существует.

2)Xi - являются детерминированными величинами и не равны все между собой.

3)εi -случайные величины причем

3.1) E (εi )= 0, i

3.2) var (εi )=σε2 , i (гомоскедастичность)

3.3) cov(εiεj )= 0 i ≠ j (не коррелированность).

Тогда МНК оценки α), β являются

1)линейными по Y

2)несмещенными

3)эффективными оценками параметров α, β

Весь наш дальнейший курс будет в основном состоять в том, что мы обобщим полученные результаты на случай нескольких объясняющих переменных, а потом будем смотреть, что изменится, если какая-нибудь из предпосылок теоремы Гаусса-Маркова не выполняется.

Рассмотрим, какими свойствами будет обладать случайная величина Y , если приведенные выше предположения справедливы.

1) E (Y Xi )=α + β Xi , так как E (εi )= 0 . В модели линейной регрессии предполагается, что математическое ожидание Y зависит от X . Хотя X и не является случайной

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон величиной, обычно пишут условное математическое ожидание. Это делается так потому,

что	в	отличии от α	и β , значение параметра X	нам известно. Если отбросить
предпосылку о том, что			X является детерминированной величиной и предположить, что
Y и	X	имеют двумерное нормальное распределение,		тогда запись E (Y	Xi )=α + β Xi

будет более уместна.

2)var (Y X )= var (Y )=σε2 , так как var (εi )=σε2 , i

3)cov(YYi j )= 0 i ≠ j , так как cov(εiεj )= 0 i ≠ j

Используя выборку из случайной величины Y и соответствующие ей значения детерминированной величины X , мы можем вычислить МНК оценки α), β) и векторы оценок Y ,e . Все они являются функциями от выборочных значений случайной величины

Y , поэтому тоже будут случайными величинами. Сейчас мы рассмотрим свойства этих четырех оценок, и при этом докажем теорему Гаусса-Маркова.

)

∑(Xi − X

) (Yi −Y

)

Вспомним, как вычисляется β (формула 2.04)

β =

i=1

, обозначим

∑(Xi − X

(Xi − X

)

i=1

w =

, и обратим внимание, что

∑(Xi − X )2

∑xi

i=1

(2.15)

∑wi = 0;

∑wi xi =

∑wi Xi =1

∑wi2

i=1

∑xi2

i=1

)

соответственно

= ∑wi (Yi −Y )= ∑wi Yi −Y ∑wi

= ∑wi

Yi -

линейность по Y β

доказана.

i=1

)

E (β)= E

∑wi Yi

= ∑wi E

(Yi )= ∑wi (α + β Xi )=α∑wi + β ∑wi Xi = 0 + β 1 = β -

i=1

несмещенность β) доказана. Докажем эффективность.

	)	N		N	N	σ2
(2.16)	var (β)= var	∑wi	Yi	= ∑wi2 var (Yi )=σε2 ∑wi2 =		ε
						N
		i=1		i=1	i=1	∑xi2
пусть b = ∑vi Yi						i=1
	- произвольная линейная несмещенная оценка параметра β найдем веса

vi , так чтобы ее дисперсия была минимальна, то есть чтобы оценка была эффективной в

классе линейных несмещенных оценок. Если при этом мы получим, что vi							совпадают с
wi , значит β)- и есть единственная эффективная оценка β .
	N		N	N	N	N
E (b)= E	∑vi	Yi	= ∑vi	E (Yi )= ∑wi	(α + β Xi )=α∑vi	+ β ∑vi Xi = β	получаем
i=1			i=1	i=1	i=1	i=1

ограничения необходимые для того, чтобы оценка была несмещенной

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

N
∑vi = 0
i=1
N
∑vi Xi =1
i=1
	N		N	N
var (b)= var	∑vi	Yi	= ∑vi2 var (Yi )=σε2 ∑vi2 , (так как cov(YiYj )= 0 ).
i=1			i=1	i=1

Задача поиска оценки с минимальной дисперсией будет иметь вид:

	N
	∑vi2 min
	i=1
(2.17)	N	= 0
(2.17)	∑vi	= 0
	i=1
	N	Xi =1
	∑vi	Xi =1
	i=1

N	N		N		,
Функция Лагранжа задачи (2.17) имеет вид: L = ∑vi2 −λ ∑vi		+ µ 1	−∑vi	Xi	,
i=1	i=1		i=1

где λ, µ множители Лагранжа. Берем производную по vi :

(2.18)	∂L	= 2 v	−λ −µ X	i	= 0

		i
	∂vi

суммируем условия первого порядка (2.18): ∑∂L = 2 ∑vi − N λ −µ ∑Xi = 0 , так как

∂vi

∑vi = 0 , то −N λ −µ ∑Xi = 0 λ = −µ X , подставляя в условие первого порядка

i=1

(2.18) получаем:

(2.19)

Умножая (2.19)

∂∂L = 2 vi −µ (Xi − X )= 0 vi

на Xi получаем 2 vi Xi −µ (Xi − X ) Xi = 0 , суммируем по всем i :

2 ∑vi

Xi −µ ∑(Xi − X

) Xi = 0 ,

вспомним,

что

∑vi

что

∑(Xi

) Xi = ∑(Xi − X

) Xi − X

∑(Xi − X

)= ∑(Xi

i=1

= ∑xi2

поэтому

− X

2 1−µ ∑xi = 0

µ =

подставляем

это

(2.19)

получаем

∑xi2

∂L

2 xi

b = ∑vi Yi =

∑xi Yi

)

= 2 vi −

= 0 vi =

∑xi2

= β -

решая

задачу

поиска

∂vi

∑xi2

эффективной оценки параметра β в классе линейных несмещенных оценок мы получили

формулу МНК оценки β)- значит эта оценка и является единственной эффективной оценкой β в этом классе. Эффективность доказали. Хотя особо умные студенты могут

возразить, что мы не можем утверждать, что, решая задачу поиска условного экстремума, мы нашли именно минимум дисперсии, а не максимум.

Задачка на дом №3. Предлагается проверить достаточные условия минимума в задаче (2.17). Надо будет выписать окаймленный Гессиан.

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

)

Разберемся

теперь

по

формуле

(2.04)

)

∑ i − X

∑wi

= ∑

α =Y

−β X =

− X

wi Yi - линейность по Y доказана.

i=1

)

E (α)

E ∑

− X wi

= ∑

− X wi

E (Yi )= ∑

− X wi

(α + β Xi )=

∑

= ∑

− X

(α + β Xi

)=α −α X ∑wi + β

i −β X ∑wi Xi

используя

соотношения

(2.15),

получаем

E (α))=α −α X

0 + β X

−β X 1 =α ,

несмещенность доказали.

)

var (α)

= var ∑

− X wi

= ∑

− X wi

var (Yi

(2.20)

=σ2

−

2 X ∑wi

− X

+ X

∑

∑ i

σε

∑xi2

для

вывода

формулы

дисперсии

использовались

соотношения

(2.15) и

некоррелированность Yi ,Yj для i ≠ j .

Задачка на дом №4. Докажите эффективность α . Это делается точно также, как мы только что делали для β).

И так мы доказали, что при выполнении условий перечисленных в теореме ГауссаМаркова α и β) являются линейными по Y , несмещенными и эффективными оценками параметров α и β .

Возникает вопрос, являются ли они состоятельными. Ответ: да. Доказать это можно например, проверив, что они совпадают с оценками метода максимального правдоподобия, которые являются состоятельными.

Обобщенная теорема Гаусса-Маркова. Предпосылки теоремы остаются без изменений, а утверждение будет звучать так: для любых чисел c, d оценка θ) = c α) +d β) ,

где α и β)	МНК	оценки параметров		α и	β , будет линейной, несмещенной		и
эффективной	оценкой		параметра θ = c α +d β . Линейность			и несмещенность	θ),
очевидно следуют из линейности и несмещенности α и β).
Задачка	на	дом	№5. Покажите,	что	θ) = c α) +d β)	является линейной	и

несмещенной оценкой параметра θ = c α +d β .

Эффективность можно доказать аналогично тому, как мы это делали для β). Но мы

лучше сделаем это позже, когда будем рассматривать многомерную регрессию, так как там в векторно-матричной форме это все получается гораздо проще и компактнее. Пока

просто посмотрим, чему равна дисперсия θ).

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

(2.21) var (θ))= var (c α) +d β))= c2 var (α))+d 2 var (β))+2 c d cov (α), β)),

var (α)), var (β))-

мы

знаем

(формулы 2.16

2.20),

осталось

вычислить

cov (α), β)):

)

cov(α, β)= cov

∑wi Yi ;∑

− X wi Yi

= ∑∑cov wi

Yi ;

−

X wj

(2.22)

i=1

i=1 j=1

σε2

N N

= ∑∑wi

−

X wj cov(Yi ;Yj )=σε

∑wi

− X wi = −σε

X ∑wi

= −

i=1 j=1

i=1

∑xi

В доказательстве (2.22) я

воспользовался

свойствами

(2.15)

тем,

что

i ≠ j

.Подставляя в (2.21) формулы (2.16), (2.20) и (2.22) имеем:

cov (Yi ;Yj )=

i = j

σ2

)

2 c2

(c X

−d )2

c2 X

2 +d 2 −2 c d X

(2.23)

var (θ )=σε N +

=σ

∑ i

θ) = c α) +d β)

Оценка

представляет

для

нас

практический

интерес,

когда

c =1, d = X

. В этом случае, это будет МНК оценка

)

, которая соответственно

=α + β X

является линейной, несмещенной и эффективной оценкой E (Y Xi )=α + β Xi . Мы можем

вычислять эту оценку как для значений Xi i =1.......

N из массива (Y , X ), по которому мы

оценивали регрессию, так и для произвольного значения X0 . Во втором случае мы получаем прогноз математического ожидания E (Y X0 ), для гипотетического случая, когда X = X0 . Подставляя в формулу (2.23) c =1, d = Xi , получаем дисперсию Yi

	)	2		1 (Xi − X		)2
	var (Yi	)=σε			∑xi2
(2.24)			N +

Из формулы (2.24) видно,		что чем сильнее Xi
							(или X0 ) отличается от X	тем больше

дисперсия Yi (или Y0 ), а значит меньше точность предсказания с помощью линейной

регрессии. Мы еще раз обратим на это внимание, когда будем строить доверительный интервал для прогноза.

Задачка на дом №6. Вычислите cov (Y)i ,Y)j ).

Мы также можем вычислить МНК оценки ошибок ei =Yi −Yi , их называют

остатками. Остатки обычно используют для проверки предпосылок теоремы ГауссаМаркова о свойствах случайного возмущения εi , то есть их фактически рассматривают

как выборку из этой случайной величины. Хотя это и не совсем правильно. Посмотрим

насколько характеристики ei совпадают с характеристикамиεi

(2.25)

E (ei )= E (Yi

−Y)i )= E (Yi

− E (Y

Xi ))= 0

Из (2.25) видим, что математическое ожидание

ei и εi

совпадают.

Вычислим теперь

дисперсию

var (ei )= var (Yi −Y)i

)= var (Yi

)+ var (Y)i )−2 cov (Yi ,Y)i

)

(2.26)

)

(Xi − X

мы знаем, что

var (Yi )=σε , и

var (Yi )=σε

(формула (2.24)), осталось

∑xi

вычислить cov (Yi ,Y)i ):

Материалы по курсу эконометрика-1. Подготовил Выдумкин Платон

cov(Yi ,Y)i )= cov(Yi ;α) + β) Xi )= cov(Yi ;α))+ Xi

cov (Yi ; β))=

(2.27)

= cov Yi

;∑

−

X wj

+ Xi

cov Yi

;∑wi

i=1

=σ2

− X w +

X w

=σ

∑xi

Внимательный читатель может обратить внимание, что

cov (Yi ,Y)i

), полученная в (2.27),

совпадает с выражением для var (Y)i )

(2.24), это не случайно. Значит, ее можно было

вычислить более простым способом

)+cov (ei ,Y)i )= var (Y)i

), так как cov (ei ,Y)i )= 0 , почему

cov (Yi ,Y)i )= cov(Y)i +ei ,Y)i

)

= cov (Y)i ,Y)i

это так будет объяснено ниже (смотри задачу №8).

Подставляя var (Yi )=σε2

(2.24) и (2.27) в (2.26) имеем:

var (e )=σ2

(2.28)

−2

=σ2

1−

−

N ∑xi

∑xi

N ∑xi

Из формулы (2.28) видим, что в отличие от εi

остатки не являются гомоскедастичными,

то есть var (ei )≠ var (ej ).

Задачка на дом №7. Вычислите cov(ei , ej

Для нас важно, что cov(ei , ej

)≠ 0 , то есть корреляция остатков в отличие от εi не

равна нулю. Это очевидно, так как остатки всегда будут линейно зависимы ведь для них

N	N
должны выполнятся условия ∑ei = 0 и ∑Xi ei = 0 . То есть независимыми среди			ei
i =1	i =1
может быть только N −2 величины. Эти две степени свободы уходят к оценкам α и β),
которые в свою очередь являются независимыми от остатков.
Задачка на дом №8.	Покажите, что	cov(ei ,α))= 0, cov (ei , β))= 0 i	и
cov (ei ,Y)j )= 0 i, j
Существует метод, который позволяет получить		N −2 оценки ошибок уравнения

регрессии, которые в случае, если выполняются все предпосылки теоремы ГауссаМаркова, по своим свойствам в точности совпадают с εi . То есть они имеют нулевое

математическое ожидание, одинаковую дисперсию и не коррелированны. Этометод рекурсивных остатков, он находится за рамками нашего курса. Желающие могут о нем прочитать в учебнике Johnston, в программе Eviews он реализован.

Остатки не нужно путать с ошибками, которые возникают при построении прогноза по модели регрессии. Между ними есть существенные различия. Пусть мы

оценили уравнение						)	)		для	i =1....N и хотим построить прогноз
оценили уравнение					регрессии Y =α + β X			i	для	i =1....N и хотим построить прогноз
					i			i
значения случайной величины Y , если X = X0 : Y0										=α + β X0 +ε0 . Он будет вычисляться,
)	)	)		, ошибка прогноза будет определяться, как
как Y	=α + β X		0	, ошибка прогноза будет определяться, как
0			0
	(2.29)				e0	=Y0 −Y0
Посмотрим,		чем		e0	отличается от	остатков			регрессии. Математическое ожидание не

изменилось: E (e0 )= 0 - такой прогноз называют несмещенным. Вычислим дисперсию

1 / 21 2 > Следующая >>>

Соседние файлы в папке Выдумкин П. Эконометрика

#
20.04.2015392.78 Кб88Часть 1 Повторения тервера.pdf
#
20.04.2015321.38 Кб97Часть 2. Однофакторная регрессия.pdf
#
20.04.2015553.85 Кб111Часть 3. Множественная регрессия..pdf
#
20.04.2015378.34 Кб129Часть 4 Мультиколлинеарность..pdf
#
20.04.2015419.45 Кб112Часть 5 GLS.pdf