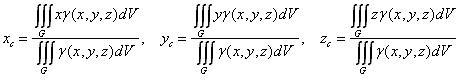4 Приложения тройных интегралов

4 Приложения тройных интегралов

4.1 Теоретическое введение

Рассмотрим приложения тройного интеграла к решению ряда геометрических задач и задач механики.

4.1.1 Вычисление площади и массы пространственного тела

Пусть в трехмерном пространстве Oxyz дано материальное тело G.  Объем V этого тела может быть найден с помощью тройного интеграла по формуле:

V = dV

(1)

Вычислим массу m тела объема V, считая, что плотность в каждой точке тела есть заданная непрерывная функция координат точки P, т.е. γ = γ(x;y;z).  Пусть в каждой точке тела G задана его объемная плотность γ = γ(x;y;z). Будем считать, что функция γ = γ(x;y;z) непрерывна в области G. Тогда масса m этого тела равна тройному интегралу от функции плотности γ = γ(x;y;z) по области G:

m =  γ(x, y, z) dV

(2)

4.1.2 Статические моменты. Центр масс пространственного тела

Статическим моментом M_xy материальной точки массы m относительно плоскости Оху называется произведение массы точки на ее координату z: M_xy = mz. Аналогично определяются статические моменты M_yz иM_xz соответственно относительно плоскостей Oyz и Oxz: M_yz = mx, ­ ­ M_xz = my.  Статические моменты пространственного тела, плотность которого равна γ(x,y,z), где γ(x,y,z) – непрерывная функция, относительно плоскости Оху вычисляется по формуле:

Mxy = zγ(x, y, z) dV

(3)

Аналогично, для статических моментов тела G относительно плоскостей Oyz и Oxz получим:

Myz = xγ(x, y, z) dV

(4)

Mxz = yγ(x, y, z) dV

(5)

Координаты x_c , y_c , z_c центра масс тела G определяются равенствами:

(6)

где m – масса тела G, которую можно найти по формуле (2). Тогда из формул (3) – (6) получим:

(7)

4.1.3 Момент инерции пространственного тела

Момент инерции I_z материальной точки массы m относительно оси Oz равен произведению массы этой точки на квадрат её расстояния до оси Oz. Так как квадрат расстояния точки P(x, y, z) до оси Oz равен x² + y², то I_z = (x² + y²) · m. Аналогично определяют моменты инерции относительно осей Ох и Оу.  Пусть дано тело G, плотность которого задана непрерывной функцией γ(x, y, z). Момент инерции этого тела относительно оси Oz может быть найден по формуле:

Jz = (x^2 + y^2) γ(x, y, z) dV

(8)

Аналогично находятся моменты инерции J_x и J_y :

Jx = (y^2 + z^2) γ(x, y, z) dV, ­ ­ ­ ­ ­ ­ Jy = (x^2 + y^2) γ(x, y, z) dV

(9)

4.2 Содержание типового расчета

Типовой расчет содержит две задачи. В каждой задаче задана пространственная область G, ограниченная поверхностями, указанными в условии задачи. Г(x,y,z) – объемная плотность области G. Для этой области найти:  1. V – объем;  2. m – массу;  3. M_yz, ­ M_xz, ­ M_xy – статические моменты относительно плоскостей Оyz, Oxz и Охy соответственно;  4. x_c, ­ y_c, ­ z_c – координаты центра масс;  5. I_z – момент инерции относительно оси Oz.

4.3 Порядок выполнения типового расчета

При решении каждой задачи необходимо:  1. Выполнить чертеж заданной области. Выбрать систему координат, в которой будут вычисляться тройные интегралы.  2. Записать область в виде системы неравенств в выбранной системе координат.  3. Вычислить объем V и массу m тела по формулам (1) и (2).  4. Вычислить статические моменты M_yz, ­ M_xz, ­ M_xy по формулам (3) – (5).  5. Вычислить координаты центра масс x_c, ­ y_c, ­ z_c по формулам (7). Нанести центр масс на чертеж. При этом возникает визуальный (качественный) контроль полученных результатов.  6. Вычислить I_z – момент инерции относительно оси Oz.  Численные ответы должны быть получены с тремя значащими цифрами.

4.4 Пример выполнения типового расчета

Задача. Пространственная область G, ограничена поверхностями z = 4 – x² – y², ­ z = 0, ­ y = 0 (y ≥ 0). Объемная плотность области G равна γ(x, y, z) = 3.  Решение. Тело ограничено поверхностью параболоида и двумя координатными плоскостями. Проекцией тела на плоскость Oxy является полукруг (рис. 1). Поэтому при вычислениях удобно использовать цилиндрическую систему координат. В этой системе уравнение параболоида запишется: z = 4 – x² – y² <=> z = 4 – ρ² и тело Gможно записать системой неравенств:  G: 

  Рис. 1

Объем тела найдем по формуле (1):  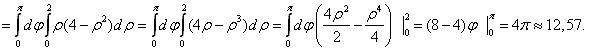    Найдем массу тела по формуле (2). Плотность его равна γ = 3= 3ρ.        Для нахождения координат центра масс вычислим сначала статические моменты тела относительно координатных плоскостей по формулам (3) – (5):                Внутренний и промежуточный интегралы здесь совпадают с соответствующими интегралами в выражении дляM_xz, поэтому переходим сразу к заключительному этапу вычисления.    Координаты центра масс найдем по формулам (6) – (7):   ­ ­ ­  ­ ­ ­   Момент инерции тела относительно оси Oz найдем по формуле (8):  J_z       Ответ: V = 4π ≈ 12,57;  M_xz = 32; M_yz = 0; x_c = 0; y_c =  z_c = J_z = 

4.5 Оформление отчета

В отчете должны быть представлены все выполненные расчеты, аккуратно выполненные чертежи. Численные ответы должны быть получены с тремя значащими цифрами.