Численное интегрирование

Задача численного интегрирования функции заключается в вычислении значений определенного интеграла, когда известен ряд значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой, двойного – механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными.

Обычный прием механической квадратуры заключается в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей или другой аппроксимирующей функцией φ(x) простого вида (например, полиномом), а затем приближенно полагают

.

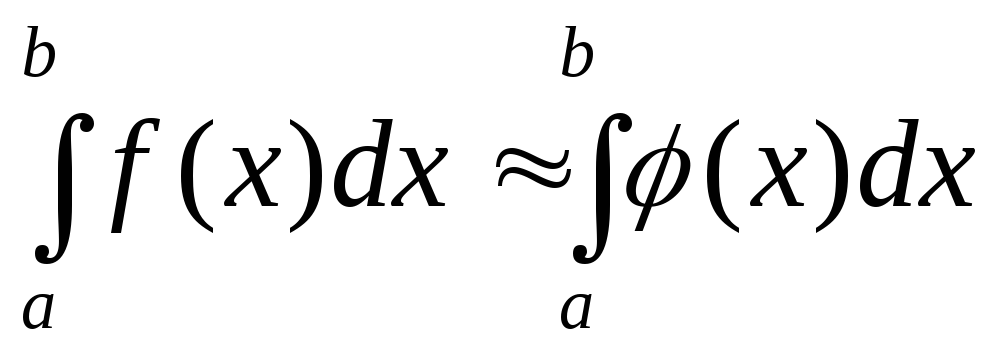Функция φ(x) такова, что интеграл от неё вычисляется напрямую с помощью формулы.

Численное интегрирование методом прямоугольников

Простейшим методом численного интегрирования является метод пря­мо­угольников, ко­то­рый в ря­де случаев оказывается на­иболее эф­фек­­­тив­­ным.

Известны три раз­но­вид­­ности метода пря­мо­у­голь­­ни­ков: это методы левых, правых и средних пря­­­мо­у­гольников. Все они основаны на ап­про­к­си­ма­­­ции подынтегральной функции f(x) прямой, проходящей через точку f(х_i), f(х_i+1) или f(х_i+/2) соответственно.

Таким образом, площадь подынтегральной кривой заменяется площадью прямоугольника:

левого прямоугольника:

;

правого прямоугольника:

;

среднего прямоугольника:

.

С учетом представления на элементарном от­­рез­ке со­став­ные формулы вычисления интегралов мо­гут быть записаны так:

левых прямоугольников:

;

правых прямоугольников:

;

средних прямоугольников:

.

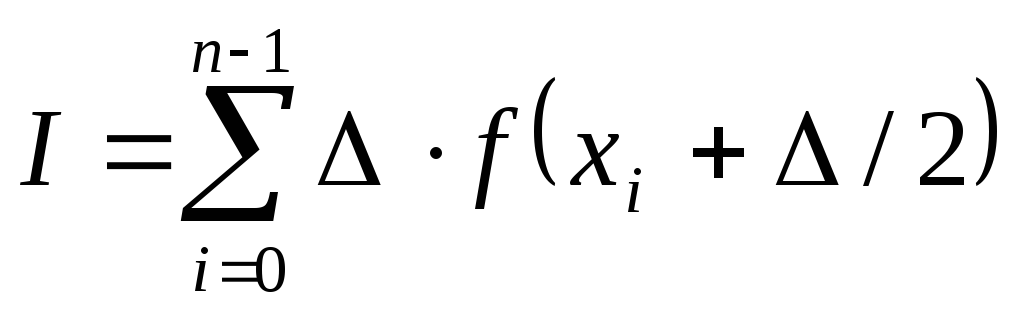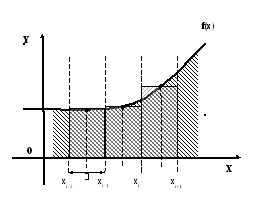
Рисунок 30 – Геометрическая интерпретация численного интегрирования методом центральных прямоугольников

Приведём программу, реализующую вычисление определённого интеграла методом центральных прямоугольников с заданным количеством разбиений. В качестве подынтегральной будем использовать функцию:

^.

program rect;

function f(x: real): real;

begin

f:=1/x

end;

var

a,b,e: real;

i: integer;

x,s,dx: real;

n: integer;

begin

writeln('[a,b],n');

readln(a,b,n);

{вычисление длины отрезка – основания прямоугольника (дельта)}

dx:=(b-a)/n;

for i:=0 to n-1 do

begin

{вычисление абсцыссы середины очередного отрезка разбиения}

x:=a+dx*i+dx/2;

s:=s+dx*f(x);

end;

writeln('int=',s);

end.

В данной программе используется подпрограмма функция f, которая вычисляет подынтегральную функцию.

Численное интегрирование методом Симпсона с заданной точностью

Принцип метода Симпсона состоит в замене под­ын­те­граль­ной функ­ции f(х) интерполяционным мно­гочленом Нью­­то­на вто­рой сте­пени. Тогда для каждого эле­мен­тар­­но­го от­резка [хi,хi+1] име­ем следующее значение площади подынтегральной кривой:

^.

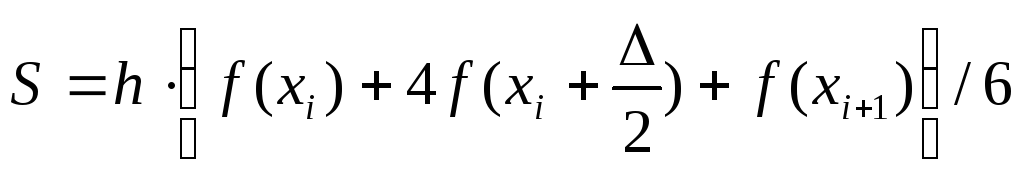Для всего отрезка интегрирования [a,b] формулой Симпсона:

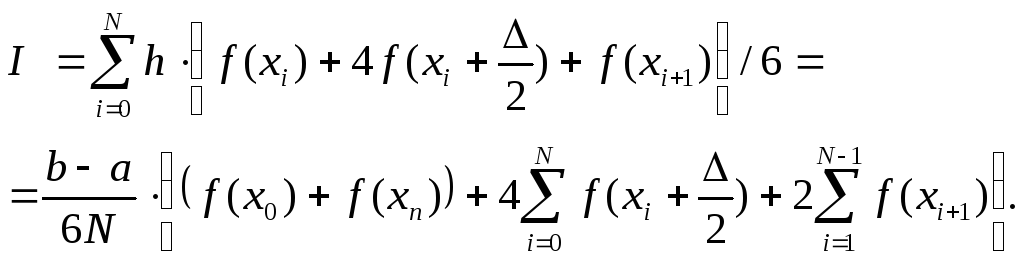
Данное выражение называется формулой Сим­сона. Оно от­носится к формулам по­вы­шен­ной точ­нос­ти и яв­ля­ется точ­ной для мно­го­чле­нов второй и третьей сте­пе­ни.

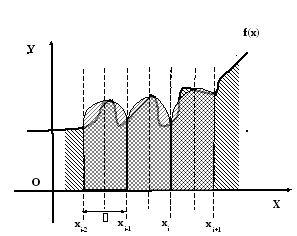
Рисунок 31 – Геометрическая интерпретация численного интегрирования методом Симпсона

Приведём программу, реализующую вычисление определённого интеграла методом Симпсона с заданной точностью. В качестве подынтегральной будем использовать функцию:

^.

Рассмотренные формулы численного интегрирования требуют чёткого указания количества разбиений отрезка интегрирования. Однако классическое использование численного метода предполагает вычисление значения (корня, интеграла и т.д.) с заданной точностью.

Точность любой формулы численного интегрирования зависит от величины отрезка разбиения .

Будем вычислять значение интеграла при разных значениях  (₁, _2, _3,…), где _i+1 = 2_i. Как только разница между значением интеграла, вычисленного при _i и интеграла, вычисленного при _i+1, станет меньше, чем значение , будем считать, что интеграл вычислен с заданной точностью .

Данный метод интегрирования с заданной точностью прост в реализации, однако он требует значительных избыточных вычислений, что приводит к повышению затрат времени на вычисление.

program simp;

function f(x: real): real;

begin

f:=1/x

end;

var

a,b,e: real;

i: integer;

xa,xab,xb,dx,s1,s: real;

n: integer;

begin

writeln('[a,b],e');

readln(a,b,e);

{вычисление интеграла с количеством разбиений равным 1, т. е. одной фигурой с основанием равным [a,b]}

n:=1;

dx:=(b-a)/n;

s:=dx*(f(a)+4*f(a+dx/2)+f(b))/6;

repeat

n:=n*2; {удвоение количества отрезков разбиения}

s1:=s;

s:=0;

{вычисление длины отрезка – основания прямоугольника (дельта) при новом количестве разбиений}

dx:=(b-a)/n;

{суммирование площадей - нахождение интеграла при заданном количестве разбиений}

for i:=0 to n-1 do

begin

xa:=a+dx*(i);

xb:=xa+dx;

xab:=xa+dx/2;

s:=s+dx*(f(xa)+4*f(xab)+f(xb))/6;

end;

until abs(s-s1)<=abs(e);

writeln('int=',s);

end.

В данной программе используется подпрограмма функция f, которая вычисляет подынтегральную функцию.

Переменная s1 используется для сохранения значения интеграла, вычисленного при вдвое меньшем количестве разбиений.