
- •«Дальневосточный федеральный университет»
- •Школа Естественных наук
- •Учебно-методический комплекс дисциплины
- •Форма подготовки - очная
- •«Дальневосточный федеральный университет»
- •Структура и содержание дисциплины
- •Состав и уравнение состояния атмосферы
- •Статика атмосферы
- •Силы, действующие в атмосфере в состоянии равновесия
- •Уравнение статики атмосферы
- •Барометрические формулы
- •Барическая ступень
- •Геопотенциал. Абсолютная и относительная высота изобарических поверхностей
- •Градиентные измерения
- •Лучистая энергия в атмосфере и на земной поверхности
- •Основные законы лучистой энергии
- •Корпускулярная радиация Солнца.
- •Интенсивность прямой солнечной радиации
- •Солнечная постоянная
- •Суммарная радиация
- •Длинноволновое излучение земной поверхности и атмосферы
- •Годовой теплооборот почвы и воды
- •Непериодические изменения температуры воздуха
- •Температуры воздушных масс
- •Междусуточная изменчивость температуры
- •Индексы континентальности
- •Тепловой баланс Земли, земной поверхности и атмосферы
- •Практическая часть курса (темы занятий, час, ссылка на литературу)
- •Самостоятельная работа студентов
- •Тема5.Солнечная радиация. Основные законы излучения. Солнечная постоянная
- •Основная литература
- •Дополнительная литература
- •Некоторые константы
Барометрические формулы
Основное уравнение статики является одним из важнейших уравнений метеорологии, на основе которого устанавливаются закономерности распределения давления, плотности и массы воздуха по высоте. В своем дифференциальном виде основное уравнение статики позволяет выполнить расчет изменения давления лишь для малых приращении высоты dz.
На практике всегда необходимо иметь данные о распределении давления в слоях атмосферы конечной толщины или определить толщину таких слоев по измеренным значениям давления. Для этой цели основное уравнение статики записывают в конечном (интегральном) виде, т.е. находят его интегралы. Интегралы основного уравнения статики атмосферы, полученные при разных предположениях относительно изменения температуры и плотности воздуха с высотой, называются барометрическими формулами. На основе этих формул решаются такие важные практические задачи, как расчет распределения давления и плотности по высоте, определение высот различных летательных аппаратов по измеренному давлению, приведение давления к уровню моря и др.
Для получения интегральной формы основного уравнения статики проинтегрируем левую и правую части уравнения
– dp = ρgdz
в пределах от уровня моря z = 0 (или земной поверхности), где давление p0 , до произвольной высоты z, где давление p. Получим интегральную форму для сухого воздух:
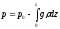 .
.
Здесь ρ = ρ(z) - функция высоты.
Вторую интегральную форму основному уравнению статики можно придать, если воспользоваться уравнением состояния влажного воздуха
p = RcρTv ,
где Rc – удельная газовая постоянная; Tv – виртуальная температура. Найдем из этого уравнения значение ρ и перепишем уравнение статики в следующем виде:
 .
.
Интегрируя в пределах от 0 до z и от p0 до p, получаем интегральную форму для влажного воздуха
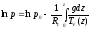 .
.
Полученные интегральные формы для сухого и влажного воздуха широко используются для получения различных барометрических формул. Причем давление p0 может обозначать как давление на уровне моря, так и на поверхности Земли. Различие будет состоять лишь в начале отсчета высоты z. В общем случае температура, а вместе с ней и плотность воздух являются достаточно сложными функциями высоты, установить аналитический вид которых далеко не всегда представляется возможным. Поэтому, прежде чем перейти к общему случаю, рассмотрим несколько частных с заданным распределением температуры по высоте. При этом обычно считают состав воздуха неизменным (μ = const) и пренебрегают изменением g с высотой, принимая g (z) = const, что, конечно, вносит некоторую неточность и допустимо до высот около 80 – 100 км.
Обычно в метеорологии рассматривают следующие частные случаи:
однородная атмосфера - плотность атмосферы ρ с высотой не изменяется;
изотермическая атмосфера – температура в атмосфере с высотой остается неизменной (T = const);
политропная
атмосфера –
температура воздуха в атмосфере убывает
с высотой по линейному закону
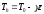 , где
, где - вертикальный температурный градиент.
- вертикальный температурный градиент.
Выделение таких случаев имеет смысл, потому, что хотя в целом для атмосферы они и неприменимы, но атмосфера до изучаемой высоты может быть разбит на ряд отдельных слоев, каждый из которых более или менее близко соответствует одному из указанных условий. Рассмотрим изменение давления при этих условиях.
Однородная
атмосфера.
Предположим, что плотность воздуха в
пределах всей атмосферы не изменяется
с высотой (однородная
атмосфера),
т.е. ρ = ρ0
= const.
Здесь ρ0
- плотность воздуха при z=0.
Пренебрежем зависимостью ускорения
свободного падения от высоты. Тогда на
основании
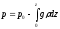 получаембарометрическую
формулу однородной атмосферы
получаембарометрическую
формулу однородной атмосферы
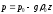
Согласно этой формуле, давление в однородной атмосфере убывает с высотой по линейному закону. В приложении к атмосфере эта формула дает далекое от реальных условий распределение давления. Однако для гидросферы, плотность которой изменяется в узких пределах (плотность воды близка к 1г/см3) она дает удовлетворительные результаты. Поэтому её можно назвать барометрической формулой гидросферы (высота в этом случае отсчитывается от дна моря или океана).
Высота
однородной атмосферы (высота
на которой давление обращается в нуль).
Высота однородной атмосферы обозначается
через H.
Согласно
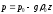 получим:
получим:
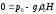 или
или
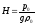
Так
как
 ,
то
,
то (T0
– температура воздуха при z
= 0) получаем
(T0
– температура воздуха при z
= 0) получаем
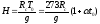
Отсюда следует, что высота однородной атмосферы конечна и зависит только от температуры воздуха на поверхности Земли. При t0 = 0ºC она составляет
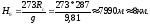
Так
как плотность в однородной атмосфере
постоянна, а давление быстро убывает с
высотой, температура её, равная по
уравнению состояния
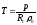 должна понижаться. Беря производную по
высоте от левой и правой части, получаем
должна понижаться. Беря производную по
высоте от левой и правой части, получаем
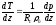
Привлекая
 ,
находим следующее выражение для
вертикального градиента температуры
γА
в однородной
атмосфере:
,
находим следующее выражение для
вертикального градиента температуры
γА
в однородной
атмосфере:
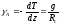 или
γА
=
3,42ºС/100 м.
или
γА
=
3,42ºС/100 м.
Таким образом, в однородной атмосфере температура убывает с высотой по линейному закону:
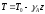 ,
,
при этом скорость понижения (градиент) значительно больше среднего значения γ в пределах тропосферы.
Изменение плотности воздуха с высотой в общем случае. Возьмем логарифмическую производную по высоте от левой и правой части уравнения состояния p = RcρT :
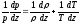 .
.
Заменив
dp/dz
по
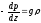 и в полученном выраженииρ
по уравнению
p
= RcρT
найдем
и в полученном выраженииρ
по уравнению
p
= RcρT
найдем
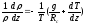 или
или
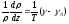 .
.
Эта формула справедлива для любого распределения температуры воздуха по высоте. На основе её можно сделать выводы относительно изменения плотности воздуха о высоте. Возможны три различных случая.
Если γ > γА = 3,42ºС/100м, то dρ /dz > 0, т.е. плотность воздуха возрастает с высотой. Вертикальные градиенты температуры γ, больше 3,42ºС/100м, в реальных условиях атмосферы могут наблюдаться лишь в дневные часы летом в приземном слое атмосферы. При таких условиях плотность в этом слое растет с высотой.
Если γ = γА, то dρ /dz = 0 т.е. плотность воздуха не изменяется с высотой: ρ = ρ0 = const. Это случай однородной атмосферы.
Если γ < γА , то dρ /dz < 0, т.е. плотность воздуха убывает с высотой. Этот случай является абсолютно преобладающим в условиях атмосферы. Прежде всего выше приземного слоя γ < γА при любых состояниях атмосферы. В приземном слое случаи когда γ < γА, наблюдаются также значительно чаще, чем случаи γ > γА. Таким образом, наиболее характерным состоянием атмосферы является такое, когда плотность воздуха убывает с высотой.
Изотермическая
атмосфера. Такая
атмосфера наблюдается при условии когда
температура с высотой не изменяется,
т.е. Т = Т0
=const,
здесь Т0
– температура на уровне моря или
поверхности Земли. Изотермическая
атмосфера по своим свойствам противоположна
однородной атмосфере. Считая атмосферу
сухой и пренебрегая зависимостью
ускорения свободного падения от высоты,
на основании
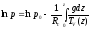 получаембарометрическую
формулу изотермической атмосферы:
получаембарометрическую
формулу изотермической атмосферы:
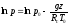 или
или ,
,
т.е. давление в изотермической атмосфере убывает с высотой по экспоненциальному закону.
Отсюда видно, что изотермическая атмосфера не имела бы верхней границы и простиралась бы до бесконечности, а на высоте z = H давление в ней уменьшилось бы только в exp раз, в то время как в однородной атмосфере на этой высоте оно было бы равно нулю.
Высоту
z,
на которой в изотермической атмосфере
давление равно pz,
можно выразить формулой
 или, учитывая
или, учитывая и переходя к десятичным логарифмам
получим
и переходя к десятичным логарифмам
получим .
ПринимаяH0
= 8000 м,
последнее уравнение перепишем в виде
.
ПринимаяH0
= 8000 м,
последнее уравнение перепишем в виде
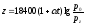
Главные выводы изотермической атмосферы
1.Если высота растет в прогрессии арифметической, то давление убывает в прогрессии геометрической.
2.При более высокой Т давление в изотермич. атм. убывает с высотой медленнее, чем при более низкой Т
3.Чем выше расположен слой атмосферы определенной толщины, тем меньше давление в этом слое.
Можно отметить, что в изотермической атмосфере давление уменьшилось бы (при t=0º) в 10 раз на высоте 18,4 км и в 100 раз на высоте около 37 км. В действительности эта высота несколько меньше, так как средняя температура такого слоя меньше нуля.
Политропная атмосфера. Политропной называют такую атмосферу, которая характеризуется линейным изменением температуры воздуха с высотой (или постоянным значением вертикального градиента температуры):
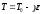 .
.
Считая
атмосферу сухой (Tv=T)
и подставляя Т в формулу
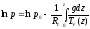 получаем
получаем
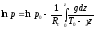 .
.
Выполнив интегрирование (в предположении g = const), приходим к барометрической формуле политропной атмосферы:
 .
.
Графически зависимость p от z изображена на рисунке. Кривые соответствуют одним и тем же значениям p и T0, но разным значениям вертикального градиента температуры: γ1 > γ2. Давление при большем значении вертикального градиента температуры (γ1) убывает с высотой быстрее, чем при меньшем (γ2).

Рисунок. Распределение давления по высоте в политропной атмосфере [Матвеев].
Для
сравнения приведены кривые изменения
давления в однородной и изотермической
атмосферах (штриховые кривые). Высота
политропной атмосферы конечна. Т.е.
согласно
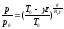 ,
давление обращается в нуль на такой
высотеz
= Hγ,
на которой
,
давление обращается в нуль на такой
высотеz
= Hγ,
на которой
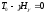 или
или
 .
.
Формула для плотности воздуха в политропной атмосфере имеет вид
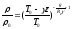 .
.
Полная барометрическая формула (формула Лапласа). Общий случай: температура распределяется произвольно по высоте, реальный воздух влажный, ускорение свободного падения – функция широты и высоты. С полным выводом уравнения можно ознакомиться на с.87 [Матвеев].
Полная барометрическая формула (Формула Лапласа) окончательно имеет вид:
 .
.
Величина
В = 2,30×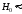 18 400
м называетсябарометрической
постоянной,
а средние значения
18 400
м называетсябарометрической
постоянной,
а средние значения
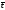 и
и носят название средних барометрических
(температуры и удельной влажности
соответственно).
носят название средних барометрических
(температуры и удельной влажности
соответственно).
В таком полном виде барометрическая формула на практике используется лишь при барометрическом нивелировании. При решении подавляющего большинства метеорологических задач такой высокой точности не требуется. Поэтому, если считать воздух сухим и пренебречь зависимостью ускорения свободного падения от широты и высоты, получим барометрическую формулу реальной атмосферы:
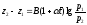
Возвращаясь
к натуральным логарифмам и абсолютной
температуре эту формулу можно записать
в виде:
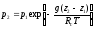 ,
где
,
где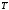 =273
(1+
=273
(1+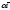 )
–средняя
барометрическая температура слоя
воздуха, заключенного между уровнями
)
–средняя
барометрическая температура слоя
воздуха, заключенного между уровнями
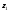 и
и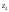 .
Средняя барометрическая температура
– это такая постоянная в пределах слоя
температура, которая обеспечивает
значения давления на границах его,
наблюдаемые при реальном распределении
температуры по высоте. Практически
.
Средняя барометрическая температура
– это такая постоянная в пределах слоя
температура, которая обеспечивает
значения давления на границах его,
наблюдаемые при реальном распределении
температуры по высоте. Практически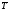 нередко отождествляют со средней
арифметической температурой, т.е.
полагают
нередко отождествляют со средней
арифметической температурой, т.е.
полагают
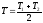 ,
,
где
 и
и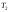 -
температуры воздуха на нижней и верхней
границах слоя. Если уровень
-
температуры воздуха на нижней и верхней
границах слоя. Если уровень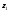 совпадает с поверхностью Земли (
совпадает с поверхностью Земли (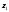 = 0), а уровень
= 0), а уровень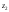 - произвольный (
- произвольный (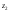 =z),
то формула
=z),
то формула
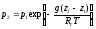 принимает вид
принимает вид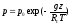 .
.
Решение задач с помощью барометрических формул:
Вычисление распределения давления по высоте. Задача состоит в определении величины давления
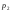 на некотором уровне
на некотором уровне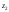 по заданному значению
по заданному значению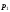 на
уровне
на
уровне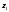 и среднему значению
и среднему значению в слое
в слое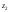 -
-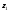 .
Обычно при этих расчетах применяются
формулы для изотермической атмосферы.
.
Обычно при этих расчетах применяются
формулы для изотермической атмосферы.Барометрическое нивелирование. Оно применяется, когда ставится задача определить разность высот двух точек
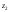 -
-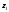 по значениям давления в них
по значениям давления в них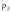 ,
,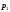 и виртуальной температуры
и виртуальной температуры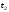 и
и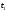 .
При необходимости получения большой
точности расчету следует вести по
формуле Лапласа. Обычно на практике
проводят вычисления по формуле для
изотермической атмосферы, используя
её последовательно для небольших слоев
(1-2км). Также используются гипсометрические
таблицы и номограммы.
.
При необходимости получения большой
точности расчету следует вести по
формуле Лапласа. Обычно на практике
проводят вычисления по формуле для
изотермической атмосферы, используя
её последовательно для небольших слоев
(1-2км). Также используются гипсометрические
таблицы и номограммы.Приведение давления к уровню моря. Известны
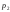 ,
, ,
,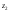 ,
,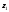 и
и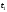 .
Требуется найти
.
Требуется найти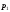 .
Эта задача имеет широкое применение в
метеорологии, когда давление
.
Эта задача имеет широкое применение в
метеорологии, когда давление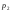 ,
наблюденное на некоторой станции на
высоте
,
наблюденное на некоторой станции на
высоте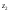 ,
приводится к давлению
,
приводится к давлению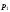 на
уровне моря. Практически это осуществляется
при помощи готовых таблиц.
на
уровне моря. Практически это осуществляется
при помощи готовых таблиц.Определение средней температуры слоя
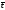 .
В этом случае известны
.
В этом случае известны
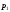 и
и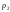 на
высотах
на
высотах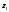 и
и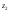 и требуется найти
и требуется найти ,
что осуществляется с помощью приведенных
выше формул.
,
что осуществляется с помощью приведенных
выше формул.
