metoda_2013

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Соотношения между типами грамматик:

(1)любая регулярная грамматика является КС-грамматикой;

(2)любая регулярная грамматика является УКС-грамматикой;

(3)любая КС-грамматика является КЗ-грамматикой;

(4)любая КС-грамматика является неукорачивающей грамматикой;

(5)любая КЗ-грамматика является грамматикой типа 0.

любая неукорачивающая грамматика является грамматикой типа

0.

Замечание: УКС-грамматика, содержащая правила вида

A , не является КЗ-грамматикой и не является неукорачивающей грамматикой.

Распознавателем для регулярной грамматики является конечный автомат (КА). Автоматами в данном контексте называют математические модели некоторых вычислительных устройств. Конечным автоматом (КА) называют кортеж следующего вида:

M(Q, V, , H, S)

Q – конечное множество состояний автомата;

V – конечное множество допустимых входных символов; H – начальное состояние автомата Q;

S – непустое множество конечных состояний автомата

– функция переходов. Находясь в некотором состоянии, функция позволяет перейти в другое состояние по данному входному символу

Конечный автомат M(Q, V, , H, S) называют

детерминированным конечным автоматом (ДКА), если в каждом из его состояний для любого входного символа есть однозначный переход из данного состояния в другое. В противном случае конечный автомат называют

недетерминированным (НКА)

Для любого НКА можно построить эквивалентный ему ДКА. При построении компиляторов чаще всего используют полностью определенный (функция переходов ДКА определена для каждого состояния автомата) ДКА.

На основе имеющееся регулярной грамматики можно построить эквивалентный ей КА, и наоборот, для заданного КА можно построить эквивалентную ему регулярную грамматику. Создав автомат на основе известной грамматики, мы получаем

220

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

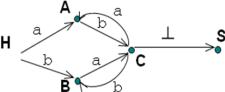
распознаватель для лексических конструкций языка. Таким образом, удается решить задачу разбора для лексических конструкций языка, заданных произвольной регулярной грамматикой. Обратное утверждение также важно, поскольку позволяет узнать грамматику, цепочки языка которой допускает заданный автомат Переход от регулярной грамматикик к конечному автомату

Граммати	Диаграмма состояний		КА
ка
S C ┴				a	b	┴
C Ab|Ba			Н	A	B
B b| Cb			А		C
A a | Ca			В	C
			С	A	B	S
			S	END

M({H, A,B, C, S}, {a,b,c, ┴}, , H, {S}), где {H, a}=A; {H,b}=B;

{A,b}=C; {B,a}=C; {C,a}=A; {C,b}=B; {C, ┴}=S

3. Практические ограничения, налагаемые на грамматики. Отношения применимые к грамматикам.

Следующие ограничения налагются на грамматики при их практическом использовании. Фактически эти условия не ограничивают множество языков, которые можно описать с помощью грамматик.

Правило, подобное U ::=U, очевидно, не является необходимым для грамматики; более того, оно приводит к неоднозначности грамматики. Поэтому далее полагается, что грамматика не содержит правил вида (1) U ::=U

Кроме того, грамматика не должна содержать цепных правил, которые приводят к зацикливанию вывода. Например,

A::=B B::=C C::=A A,B,C -нетерминалы.

Грамматики могут также содержать лишние правила, которые невозможно использовать в выводе хотя бы одного предложения. Например, в следующей ниже грамматике G[4] нетерминал <d> не может быть использован в выводе какого – либо предложения, так как он не встречается ни в одной из правых частей правил:

Z ::= <b> e

<a> ::= <a> e | e <b> ::= <c> e | <a> f <c> ::= <c> f

221

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

<d> ::= f

Разбор предложений грамматики выполняется проще, если грамматика не содержит лишних правил. Можно с достаточным основанием утверждать, что если грамматика языка программирования содержит лишние правила, то она ошибочна. Следовательно, алгоритм, который обнаруживает лишние правила в грамматике, может оказаться полезным при проектировании языка.

Чтобы появиться в выводе какого–либо предложения, нетерминал U должен удовлетворять двум условиям. Во–первых, символ U должен встречаться в некоторой сентенциальной форме: (2) Z *xUy для некоторых цепочек x и y, где Z - начальный символ грамматики. Во-вторых, из U должна выводиться цепочка t, состоящая из терминальных символов: (3) U +t для некоторой t VT+ .

Если нетерминальный символ U не удовлетворяет этим условиям, то правила, содержащие U в левой части, не могут быть использованы ни в каком выводе. С другой стороны, если все нетерминалы удовлетворяют этим условиям, то грамматика не содержит лишних правил. Так, если U ::=u – правило, то, во – первых, Z *xUy x u y. Во-вторых, так как мы можем вывести цепочку терминальных символов для каждого нетерминала, содержащего в цепочке x u y, то x u y * t для некоторой t принадлежащей VT+ .В конечном итоге мы получаем Z +t, то есть вывод, в котором было использовано правило U ::=u.

( + (“порождает”)- транзитивное замыкание(если aRb и bRc, то aRc) отношения . v *W, если v +w или v=w).

Условие (2) проверяет нетерминалы на недостижимость. Нетерминалы, которые не появляются ни в одной цепочке, выводимой из начального символа, называются недостижимыми нетерминалами.

Условие (3) проверяет нетерминалы на бесплодность. Нетерминалы, которые не порождают ни одной терминальной цепочки, называются бесплодными или мертвыми.

Нетерминалы, которые бесплодны или недостижимы, называются лишними.

В описанной выше грамматике G4 нетерминальный символ <c> не удовлетворяет условию (3), так как при непосредственном выводе он должен быть заменен на <c> f. Такая замена не может привести к цепочке из терминальных символов. Если отбросить все правила, которые нельзя использовать при порождении хотя бы одного предложения, то останутся правила Z ::= <b> e, <a> ::=

<a> e, <a> ::= e, <b> ::= <a> f .

222

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Грамматика G называется приведенной, если каждый нетерминал U удовлетворяет условиям (2) и (3), то есть не содержит лишних нетерминалов.

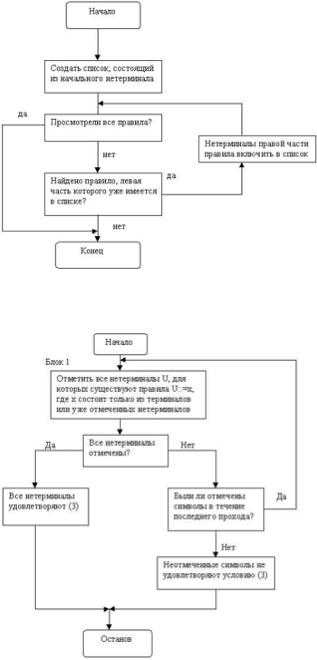
Нетерминал U удовлетворяет условию 2, тогда и только тогда, когда Z WITHIN+ U, где WITHIN+ является транзитивным замыканием отношения WITHIN (внутри). U WITHIN S тогда и только тогда, когда существует правило U ::=...S... Другими словами, если нетерминал в левой части правила является достижимым, то достижимы и все символы правой части этого правила. Это свойство выполняется, так как можно сначала вывести цепочку, содержащую символ, который является левой частью правила, и потом применить к ней это правило. Список, полученный в результате работы блок-схемы 1, содержит только достижимые нетерминалы, а все нетерминалы, не попавшие в этот список являются недостижимыми.

На рис.2 приведена блок схема алгоритма, который проверяет нетерминалы, встречающиеся в наборе правил на продуктивность (проверка условия (3)). Терминальный или нетерминальный символ называется продуктивным, если из него выводится какая-нибудь терминальная цепочка (то есть он не является бесплодным терминалом). Работа алгоритма начинается с того, что некоторым образом отмечаются те нетерминалы, для которых существует правило U ::= t , где t принадлежит VT+ (первое выполнение блока 1). Такие нетерминалы, очевидно удовлетворяют условию (3). Далее в алгоритме проверяются все неотмеченные нетерминалы U и для каждого из них делается попытка найти правило U ::= x, где x состоит только из терминальных символов или ранее отмеченных нетерминалов (повторное выполнение блока 1). Символы, для которых такое правило существует, также, очевидно удовлетворяют условию (3). Этот процесс продолжается до тех пор, пока либо все нетерминалы не будут отмечены, либо пока при выполнении блока 1 не будет отмечено ни одного символа. Работа алгоритма завершена. Неотмеченные нетерминалы не удовлетворяют условию (3).

223

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

рис 1 Проверка на достижимость:

рис 2 Проверка на продуктивность:

224

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Отношения применимые к грамматикам.

Символы “=>” и “=> +” являются примерами отношений между цепочками символов.

Вообще говоря, (бинарным) отношением на множестве является любое свойство, которым обладают (или не обладают) любые два упорядоченных символа этого множества.

Другим примером является отношение МЕНЬШЕ ЧЕМ (<), определенное на множестве целых чисел: i< j тогда и только тогда, когда j – i является положительным ненулевым целым числом. Нематематическим является отношение ДРУГ, определенное на множестве людей. Некто А либо является другом В, либо нет.

Для отношений используются следующие обозначения: если между элементами c и d некоторого множества имеет место отношение, то мы пишем cRd (при этом важен порядок двух объектов: из cRd автоматически не следует dRc).

Можно также рассматривать отношение как множество упорядоченных пар, для которых данное отношение справедливо: (c, d) принадлежит R тогда и только тогда, когда cRd.

Говорят, что отношение P включает другое отношение R, если из

(c,d) Є R следует (c,d) Є P.

Отношение, обратное отношению R, записывается как R-1 и определяется следующим образом: с R-1 d тогда и только тогда, когда dRc.

Отношение, обратное отношению БОЛЬШЕ ЧЕМ, есть МЕНЬШЕ ЧЕМ. Отношение, обратное отношению РЕБЕНОК, есть РОДИТЕЛЬ.

Свойства отношений.

Отношение R называется рефлексивным, если cRc справедливо для всех элементов c, принадлежащих множеству. Например, отношение МЕНЬШЕ ЧЕМ ИЛИ РАВНО (=< ) является рефлексивным (i =< j для всех действительных чисел i), тогда как отношение МЕНЬШЕ ЧЕМ таковым не является.

Отношение R называется симметричным, если aRb и bRa справедливо для всех элементов c, принадлежащих множеству. Например, отношение РАВНО.

Отношение R называется транзитивным, если aRb и bRc влечет за собой aRc. Отношение МЕНЬШЕ ЧЕМ над целыми числами является транзитивным.

Например, рассмотрим отношения P и R над целыми числами, определенные следующим образом:

ARb тогда и только тогда, когда b=a+1, APb тогда и только тогда, когда b=a+2.

225

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Очевидно, что aRPb, тогда и только тогда, когда есть такое c, что aRc и cRb, то есть тогда и только тогда, когда b=a+3.

Аналогично можно определить степень отношения Rn ,как произведение n отношений R, т.е. степень отношения R

формально выражается		следующим образом:			R1=R,	R2=RR,
Rn=Rn-1R=RRn-1	для n >1, т.о. aRnb означает, что существуют
a1,a2,..an-1	такие,	что	a1Ra2,	a2Ra3…		an-1Rb…
Определим R0	как единичное отношение: aR0b тогда и только
тогда, когда a=b.				R+
И, наконец,	транзитивное		замыкание		отношения R

определяется следующим образом: aR+b тогда и только тогда, когда aRnb для некоторого n>0.

Оно называется так потому, что включается в любое транзитивное отношение, которое включает в себя R. Другими словами, предположим, что P- транзитивное отношение, которое включает в себя R: и из того, что (c, d) Є R следует (c, d) Є P. Тогда P также включает в себя R+.

Очевидно, если aRb, то aR+b. Ясно, почему для транзитивного замыкания выбрано обозначение R+; когда

отношения рассматриваются как множества упорядоченных пар, мы имеем R+=R1U R2U R3U ….

Определим рефлексивное транзитивное замыкание R*

отношения R как aR*b тогда и только тогда, когда a=b или aR+b. Таким образом, R*= R0U R1U R2U … Легко доказать, что, если отношение R определено на конечном множестве A. то R+=R1UR2UR3U ….Rn, где n мощность множества A. Это утверждение для нас будет важным в дальнейшем.

Если задана грамматика и нетерминальный символ U, то нам необходимо знать множество головных символов в цепочках, выводимых из U. Определим отношение FIRST (первый) в конечном словаре V грамматики следующим образом:

U FIRST S тогда и только тогда, когда существует правило

U::=S…

(Тремя точками (…) обозначается цепочка (возможно пустая), которая в данный момент нас не интересует.)

Затем, согласно определению транзитивного замыкания, имеем: U FIRST+ S тогда и только тогда, когда существует непустая последовательность правил U::= S1…, S1::=S2…,…,Sn::=S….

Из этого, очевидно, вытекает, что U FIRST+ S тогда и только тогда, когда U=> +S….

Пример. Чтобы проиллюстрировать оба отношения FIRST и FIRST+ , выпишем несколько правил и справа от каждого из них укажем отношение FIRST, выведенное из этого правила.

226

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Правило	Отношение
A::=Af	A	FIRST	A
A::=B	A	FIRST	B
B::=DdC	B	FIRST	D
B::=De	B	FIRST	D
C::=e	C	FIRST	e
D::=Bf	D		FIRST
	B

Таким образом, мы имеем следующие пары в FIRST+: (A,A) (A,B) (A,D) (B,B) (B,D) (D,B) (D,D) (C,e).

Следовательно, головными символами цепочек, выводимых из A, будут A, B, D из B-B и D, из С-е.

Имеется еще три других множества, которые могут быть определены тем же путем, что и FIRST+. Первое из них – множество символов, которыми оканчиваются цепочки, выводимые из некоторого символа U. Они определяются для всех символов U через отношение LAST+, являющееся транзитивным замыканием отношения LAST (последний).

4. Синтаксический анализ. Синтаксические деревья. Задача

разбора. Однозначность разбора. Канонический разбор. Основа. Разбор сверху вниз, снизу вверх.

Синтаксический анализ – это процесс, который определяет, принадлежит ли некоторая последовательность лексем языку, порождаемому грамматикой.

Анализаторы реально используемых языков обычно имеют линейную сложность; это достигается, например, за счет просмотра исходной программы слева направо с заглядыванием вперед на один терминальный символ (лексический класс).

Цепочка принадлежит языку, порождаемому грамматикой, только в том случае, если существует ее вывод из цели этой грамматики. Процесс построения такого вывода (а, следовательно, и определения принадлежности цепочки языку) называется разбором.

С практической точки зрения наибольший интерес представляет разбор по контекстно-свободным грамматикам. Их порождающей мощности достаточно для описания большей части синтаксической структуры языков программирования, для различных подклассов КС-грамматик имеются хорошо разработанные практически приемлемые способы решения задачи разбора.

227

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ

Рассмотрим основные понятия и определения, связанные с разбором по КС-грамматике.

Вывод цепочки (VT)* из S VN в КС-грамматике

G = (VT, VN, P, S), называется левым (левосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого левого нетерминала.

Вывод цепочки (VT)* из S VN в КС-грамматике

G = (VT, VN, P, S), называется правым (правосторонним), если в этом выводе каждая очередная сентенциальная форма получается из предыдущей заменой самого правого нетерминала.

В грамматике для одной и той же цепочки может быть несколько выводов, эквивалентных в том смысле, что в них в одних и тех же местах применяются одни и те же правила вывода, но в различном порядке.

Например, для цепочки a+b+a в грамматике

G = ({a,b,+}, {S,T}, {S -> T | T+S; T-> a | b}, S)

можно построить выводы:

(1)S→T+S| T+T+S| T+T+T| a+T+T| a+b+T| a+b+a

(2)S→T+S| a+S| a+T+S| a+b+S| a+b+T| a+b+a

(3)S→T+S| T+T+S| T+T+T| T+T+a| T+b+a| a+b+a

Здесь (2) - левосторонний вывод, (3) - правосторонний, а (1) не является ни левосторонним, ни правосторонним, но все эти выводы являются эквивалентными в указанном выше смысле.

Для КС-грамматик можно ввести удобное графическое представление вывода, называемое деревом вывода, причем для всех эквивалентных выводов деревья вывода совпадают.

Дерево называется деревом вывода (или деревом разбора) в КС-

грамматике G = {VT, VN, P, S), если выполнены следующие условия:

(1)каждая вершина дерева помечена символом из множества (VN VT ), при этом корень дерева помечен символом S; листья - символами из (VT );

(2)если вершина дерева помечена символом A VN, а ее непосредственные потомки - символами a1, a2, ... , an, где каждое

ai (VT VN), то A → a1a2...an - правило вывода в этой грамматике;

(3) если вершина дерева помечена символом A VN, а ее единственный непосредственный потомок помечен символом , то A → - правило вывода в этой грамматике.

228

ТЕОРИЯ ЯЗЫКОВ ПРОГРАММИРОВАНИЯ И МЕТОДЫ ТРАНСЛЯЦИИ
Синтаксические	деревья	помогают	понять	синтаксис

предложений. В качестве примера рассмотрим следующую грамматику G1, содержащую 13 правил:

<число> ::= <чс>

<чс>	::=	<чс> <цифра>
<чс>	::=		<цифра>
<цифра> ::=			0 | 1 | 2 |	3 | 4 | 5 | 6 | 7 | 8 | 9

Построим синтаксическое дерево для следующего вывода предложения грамматики G1:

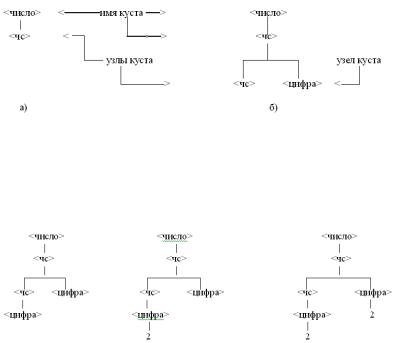
<число> => <чс> =><чс> <цифра>=><цифра><цифра>=>2<цифра>=>22 (1) Отправляясь от начального символа <число>, нарисуем его куст для того, чтобы указать первый непосредственный вывод (рис.1 а). Куст узла – это множество подчиненных ему узлов (символов). Символы куста образуют цепочку, которая заменяет имя куста в первом непосредственном выводе <число> ::= <чс>.

Рис. 1. Синтаксические деревья для двух выводов.

Чтобы показать второй вывод, из узла, представляющего заменяемый символ рисуется куст, узлы которого образуют цепочку, заменяющую этот символ (рис.1 б). Поступая таким же образом, мы построим одну за другой три синтаксические диаграммы, показанные на рис. 2.

а) б) в)

Рис. 2. Синтаксические деревья для вывода (1).

229